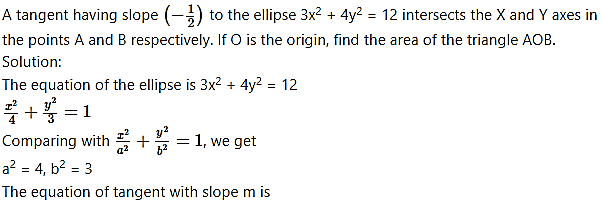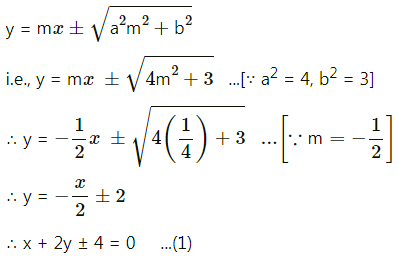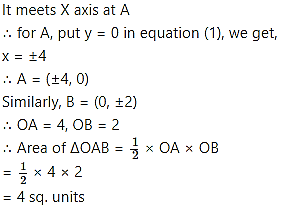Maharashtra Board Class 11 Maths Part 1 Chapter 7 Conic Sections Ex 7.2 Solution

Question 1.
Find the
(i) lengths of the principal axes
(ii) co-ordinates of the foci
(iii) equations of directrices
(iv) length of the latus rectum
(v) distance between foci
(vi) distance between directrices of the ellipse:

a = 5 and b = 3
Since a > b,
X-axis is the major axis and Y-axis is the minor axis.

(i) Length of major axis = 2a = 2(5) = 10
Length of minor axis = 2b = 2(3) = 6
Lengths of the principal axes are 10 and 6.

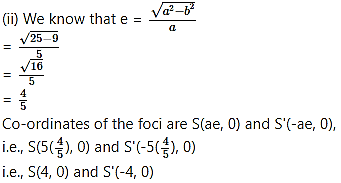
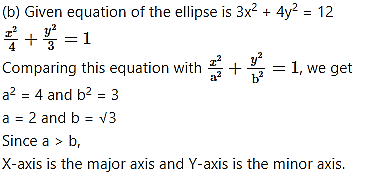
(i) Length of major axis = 2a = 2(2) = 4
Length of minor axis = 2b = 2√3
Lengths of the principal axes are 4 and 2√3.

a = √3 and b = 1
Since a > b,
X-axis is the major axis and Y-axis is the minor axis.

(i) Length of major axis = 2a = 2√3
Length of minor axis = 2b = 2(1) = 2
Lengths of the principal axes are 2√3 and 2.

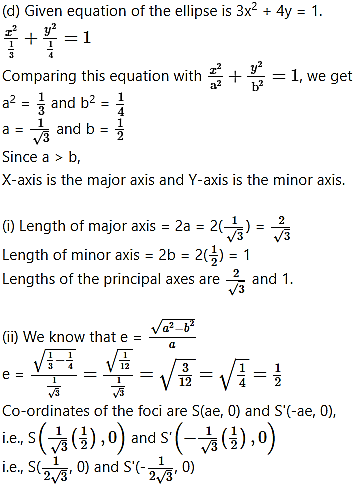
Question 2.



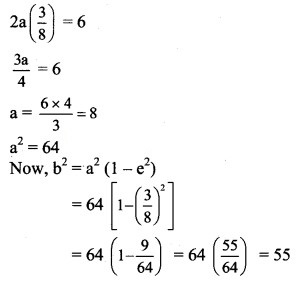
Distance between foci = 2ae
Given, distance between foci = 8
2ae = 8
2(5)e = 8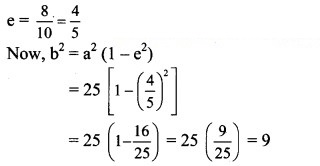

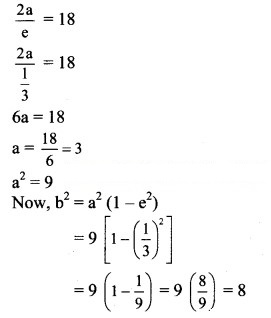
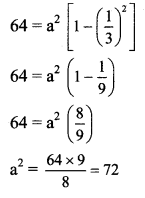
(vi) Given, the length of the latus rectum is 6, and co-ordinates of foci are (±2, 0).
The foci of the ellipse are on the X-axis.

The ellipse passes through the points (-3, 1) and (2, -2).
Substituting x = -3 and y = 1 in equation of ellipse, we get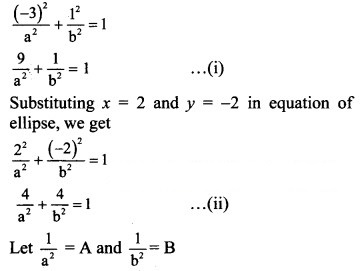

Equations (i) and (ii) become
9A + B = 1 …..(iii)
4A + 4B = 1 …..(iv)
Multiplying (iii) by 4, we get
36A + 4B = 4 …..(v)
Subtracting (iv) from (v), we get
32A = 3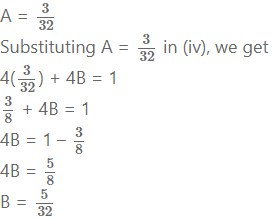

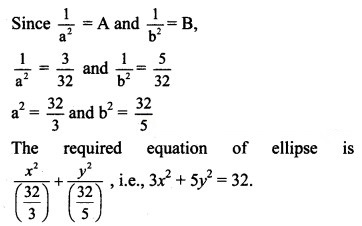
The ellipse passes through (-√5, 2).
Substituting x = -√5 and y = 2 in equation of ellipse, we get

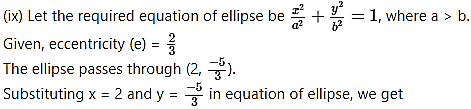
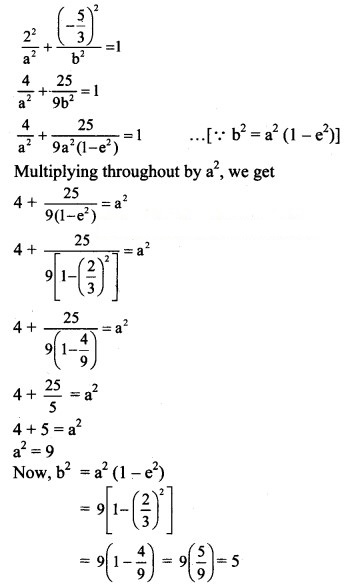
Question 3.
Find the eccentricity of an ellipse, if the length of its latus rectum is one-third of its minor axis.
Solution: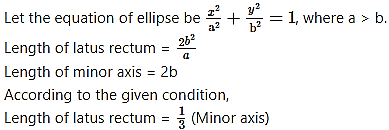

Question 4.
Find the eccentricity of an ellipse, if the distance between its directrices is three times the distance between its foci.
Solution:

Question 5.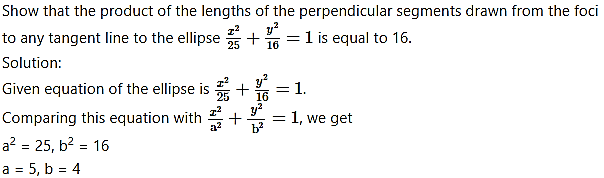

Question 6.

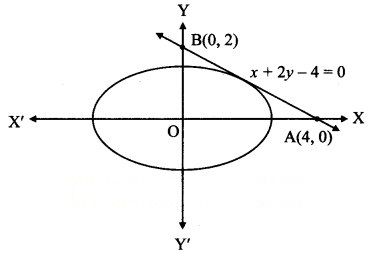
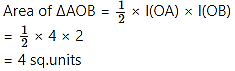
Question 7.

Question 8.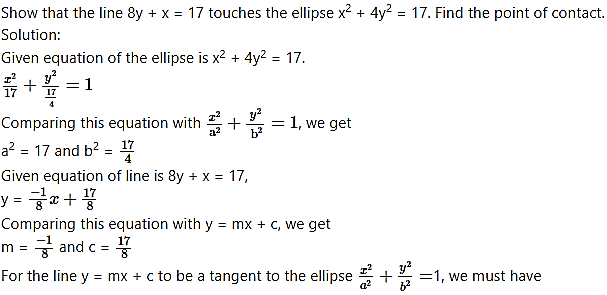

Question 9.

Question 10.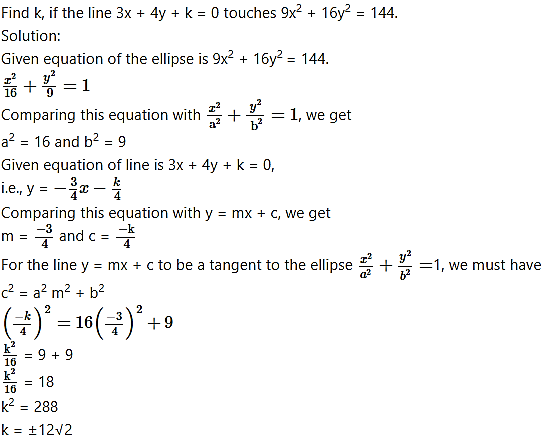

Question 11.

Solution:

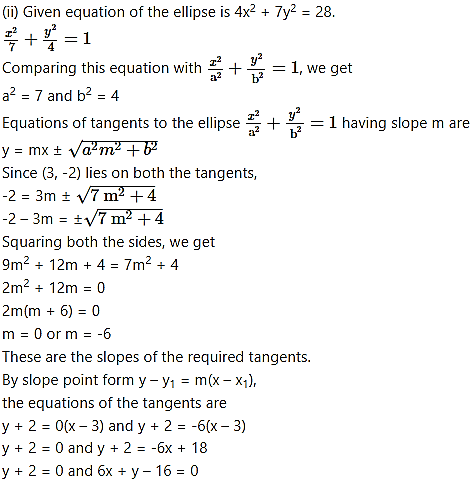
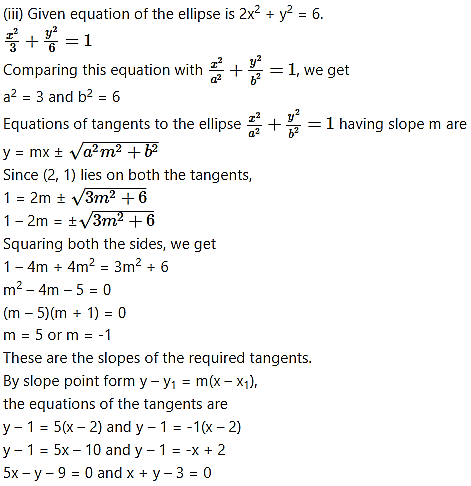
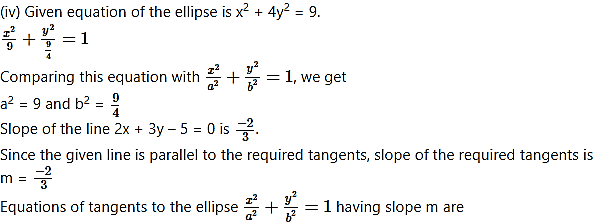
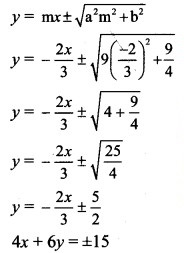
Slope of the given line x + y + 1 = 0 is -1.
Since the given line is parallel to the required tangents,
the slope of the required tangents is m = -1.
Equations of tangents to the ellipse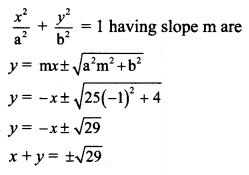

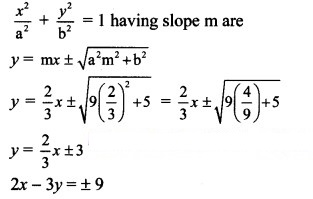
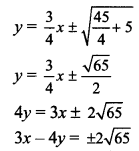
Question 12.

Alternate method:
The locus of the point of intersection of perpendicular tangents is the director circle of an ellipse.

Question 13.

Question 14.
Show that the locus of the point of intersection of tangents at two points on an ellipse, whose eccentric angles differ by a constant, is an ellipse.
Solution:

Question 15.

Question 16.

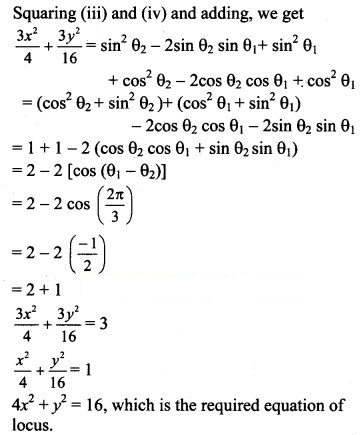
Question 17.

Question 18.