(I) Select the correct option from the given alternatives.
Question 1.
Question 2.
The length of latus rectum of the parabola – 4x – 8y + 12 = 0 is ________
(A) 4
(B) 6
(C) 8
(D) 10
Answer:
(C) 8
Hint:
Given equation of parabola is
Question 3.
If the focus of the parabola is (0, -3), its directrix is y = 3, then its equation is ________
Hint:

Question 4.
The co-ordinates of a point on the parabola y2 = 8x whose focal distance is 4 are ________![]()
(B) (1, ±2√2)
(C) (2, ±4)
(D) none of these
Answer:
(C) (2, ±4)
Question 5.
The end points of latus rectum of the parabola y2 = 24x are ________
(A) (6, ±12)
(B) (12, ±6)
(C) (6, ±6)
(D) none of these
Answer:
(A) (6, ±12)
Question 6.
Equation of the parabola with vertex at the origin and directrix with equation x + 8 = 0 is ________
(A) = 8x
(B) = 32x
(C) = 16x
(D) = 32y
Answer:
(B) = 32x
Hint:
Since directrix is parallel to Y-axis,
The X-axis is the axis of the parabola.
Let the equation of parabola be = 4ax.
Equation of directrix is x + 8 = 0
∴ a = 8
∴ required equation of parabola is = 32x
Question 7.
The area of the triangle formed by the lines joining the vertex of the parabola x2 = 12y to the endpoints of its latus rectum is ________
(A) 22 sq. units
(B) 20 sq. units
(C) 18 sq. units
(D) 14 sq. units
Answer:
(C) 18 sq. units
Hint:
= 12y
4b = 12
b = 3

Question 8.

Question 9.
The equation of the parabola having (2, 4) and (2, -4) as end points of its latus rectum is ________
(A) = 4x
(B) = 8x
(C) = -16x
(D) = 8y
Answer:
(B) = 8x
Hint:
The given points lie in the 1st and 4th quadrants.
∴ Equation of the parabola is = 4ax
End points of latus rectum are (a, 2a) and (a, -2a)
∴ a = 2
∴ required equation of parabola is y = 8x
Question 10.
If the parabola = 4ax passes through (3, 2), then the length of its latus rectum is ________
Question 11.
Question 12.
Question 14.
If the line 4x – 3y + k = 0 touches the ellipse 5 + 9 = 45, then the value of k is
(A) 21
(B) ±3√21
(C) 3
(D) 3(21)
Answer:
(B) ±3√21
Question 15.
The equation of the ellipse is 16 + 25 = 400. The equations of the tangents making an angle of 180° with the major axis are
(A) x = 4
(B) y = ±4
(C) x = -4
(D) x = ±5
Answer:
(B) y = ±4
Question 16.
The equation of the tangent to the ellipse 4 + 9 = 36 which is perpendicular to 3x + 4y = 17 is
(A) y = 4x + 6
(B) 3y + 4x = 6
(C) 3y = 4x + 6√5
(D) 3y = x + 25
Answer:
(C) 3y = 4x + 6√5
Question 17.
Question 18.
Question 19.
If the line 2x – y = 4 touches the hyperbola 4 – 3 = 24, the point of contact is
(A) (1, 2)
(B) (2, 3)
(C) (3, 2)
(D) (-2, -3)
Answer:
(C) (3, 2)
Question 20.
The foci of hyperbola 4 – 9 – 36 = 0 are
(A) (±√13, 0)
(B) (±√11, 0)
(C) (±√12, 0)
(D) (0, ±√12)
Answer:
(A) (±√13, 0)
II. Answer the following.
Question 1.
For each of the following parabolas, find focus, equation of file directrix, length of the latus rectum and ends of the latus rectum.

Question 2.
Find the cartesian co-ordinates of the points on the parabola = 12x whose parameters are
(i) 2
(ii) -3
Solution:
Given equation of the parabola is = 12x
Comparing this equation with = 4ax, we get
4a = 12
∴ a = 3
If t is the parameter of the point P on the parabola, then
P(t) = (a, 2at)
i.e., x = a and y = 2at …..(i)
(i) Given, t = 2
Substituting a = 3 and t = 2 in (i), we get
x = 3(2 and y = 2(3)(2)
x = 12 and y = 12
∴ The cartesian co-ordinates of the point on the parabola are (12, 12).
(ii) Given, t = -3
Substitùting a = 3 and t = -3 in (i), we get
x = 3(-3 and y = 2(3)(-3)
∴ x = 27 and y = -18
∴ The cartesian co-ordinates of the point on the parabola are (27, -18).
Question 3.
Find the co-ordinates of a point of the parabola = 8x having focal distance 10.
Solution:
Given equation of the parabola is = 8x
Comparing this equation with = 4ax, we get
4a = 8
∴ a = 2
Focal distance of a point = x + a
Given, focal distance = 10
x + 2 = 10
∴ x = 8
Substituting x = 8 in = 8x, we get
= 8(8)
∴ y = ±8
∴ The co-ordinates of the points on the parabola are (8, 8) and (8, -8).
Question 4.
Find the equation of the tangent to the parabola = 9x at the point (4, -6) on it.
Solution:
Given equation of the parabola is = 9x
Comparing this equation with = 4ax, we get
4a = 9
Question 5.
Find the equation of the tangent to the parabola = 8x at t = 1 on it.
Solution:
Given equation of the parabola is = 8x
Comparing this equation with = 4ax, we get
4a = 8
a = 2
t = 1
Equation of tangent with parameter t is yt = x + a
∴ The equation of tangent with t = 1 is
y(1) = x + 2(1
y = x + 2
∴ x – y + 2 = 0
Question 6.
Find the equations of the tangents to the parabola = 9x through the point (4, 10).
Solution:
Given equation of the parabola is = 9x
Comparing this equation with = 4ax, we get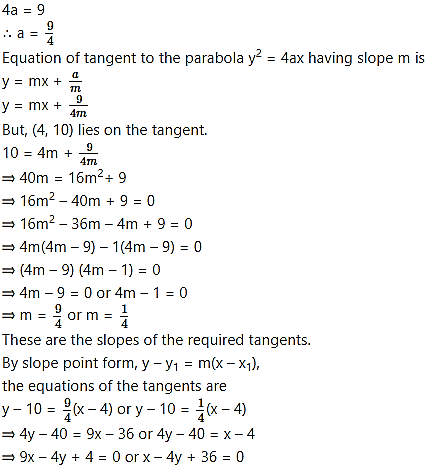
Question 7.
Alternate method:
Comparing the given equation with = 4ax, we get
4a = 24
⇒ a = 6
Equation of the directrix is x = -6.
The given point lies on the directrix.
Since tangents are drawn from a point on the directrix are perpendicular,
Tangents drawn to the parabola = 24x from the point (-6, 9) are at the right angle.
Question 8.
Question 9.
A line touches the circle + = 2 and the parabola = 8x. Show that its equation is y = ±(x + 2).
Solution:
Given equation of the parabola is = 8x
Comparing this equation with = 4ax, we get
4a = 8
a = 2
Question 10.
Two tangents to the parabola = 8x meet the tangents at the vertex in P and Q. If PQ = 4, prove that the locus of the point of intersection of the two tangents is = 8(x + 2).
Solution:
Given parabola is = 8x
Comparing with = 4ax, we get,
4a = 8
⇒ a = 2

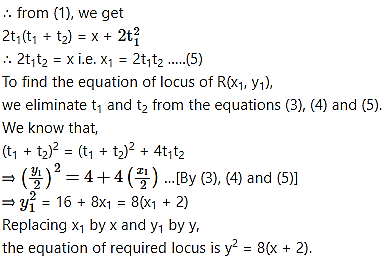
Question 11.





∴ SP subtends a right angle at Q.
Question 13.
Find the
(i) lengths of the principal axes
(ii) co-ordinates of the foci
(iii) equations of directrices
(iv) length of the latus rectum
(v) Distance between foci
(vi) distance between directrices of the curve
∴ a = 5 and b = 3
Since a > b,
X-axis is the major axis and Y-axis is the minor axis.
(i) Length of major axis = 2a = 2(5) = 10
Length of minor axis = 2b = 2(3) = 6
∴ Lengths of the principal axes are 10 and 6.
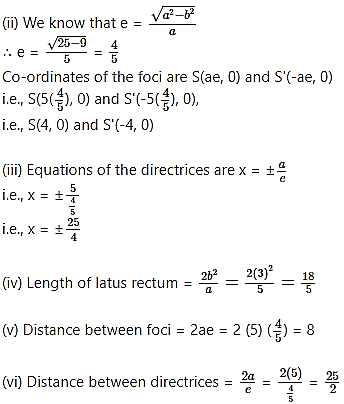
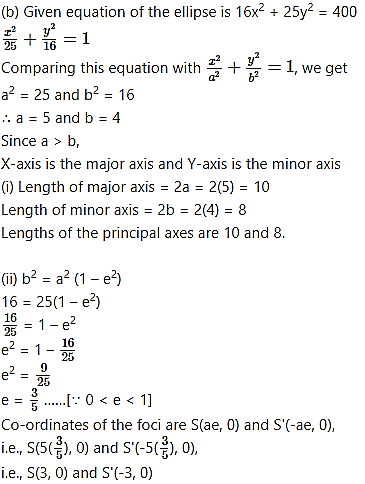



(ii) We know that
Co-ordinates of foci are S(ae, 0) and S'(-ae, 0),
i.e., S(4√2, 0) and S'(-4√2, 0)

Question 14.


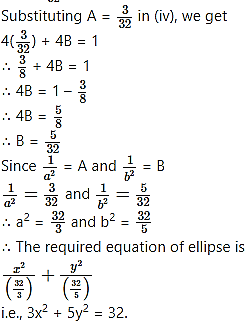
Question 15.
Find the eccentricity of an ellipse if the distance between its directrices is three times the distance between its foci.
Solution:
Question 16.
i.e., S(5√5, 0) and S'(-5√5, 0)
Since S, A and S’ lie on the X-axis,
SA = |5√5 – 10| and S’A = |-5√5 – 10|
= |-(5√5 + 10)|
= |5√5 + 10|
∴ SA . S’A = |5√5 – 10| |5√5 + 10|
= |(5√5)2 – (10)2|
= |125 – 100|
= |25|
SA . S’A = 25
Question 17.
Squaring both the sides, we get
4 + 8m + 4 = 5 + 4
∴ – 8m = 0
∴ m(m – 8) = 0
∴ m = 0 or m = 8
These are the slopes of the required tangents.
∴ By slope point form y – = m(x – ),
the equations of the tangents are
y + 2 = 0(x – 2) and y + 2 = 8(x – 2)
∴ y + 2 = 0 and y + 2 = 8x – 16
∴ y + 2 = 0 and 8x – y – 18 = 0.
Question 18.
Solution:

Question 20.
∴ xy = – 5
∴ – xy – 5 = 0, which is the required equation of the locus of P.
Question 21.
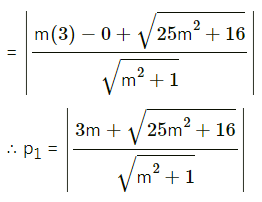
p2 = length of perpendicular segment from S'(-3, 0) to the tangent (i)
Question 22.
Find the equation of the hyperbola in the standard form if
(i) Length of conjugate axis is 5 and distance between foci is 13.
(ii) eccentricity is 2/3 and distance between foci is 12.
(iii) length of the conjugate axis is 3 and the distance between the foci is 5.
Solution:


Question 23.

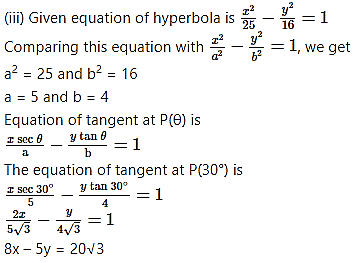
Question 24.
Question 25.
Question 26.
