Chapter 1 Similarity Set 1.2

Question 1.
Given below are some triangles and lengths of line segments. Identify in which figures, ray PM is the bisector of ∠QPR.

Solution:

Question 2.
In ∆PQR PM = 15, PQ = 25, PR = 20, NR = 8. State whether line NM is parallel to side RQ. Give reason.

Solution:
PN + NR = PR [P – N – R]
∴ PN + 8 = 20
∴ PN = 20 – 8 = 12
Also, PM + MQ = PQ [P – M – Q]
∴ 15 + MQ = 25

∴ line NM || side RQ [Converse of basic proportionality theorem]

Question 3.
In ∆MNP, NQ is a bisector of ∠N. If MN = 5, PN = 7, MQ = 2.5, then find QP.

Solution: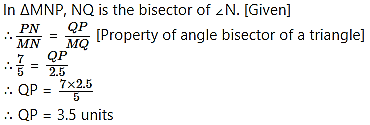

Question 4.


Solution:
Proof
∠APQ = ∠ABC = 60° [Given]
∴ ∠APQ ≅ ∠ABC
∴ side PQ || side BC (i) [Corresponding angles test]
In ∆ABC,
sidePQ || sideBC [From (i)]

Question 5.
In trapezium ABCD, side AB || side PQ || side DC, AP = 15, PD = 12, QC = 14, find BQ.

Solution:
side AB || side PQ || side DC [Given]

Question 6.
Find QP using given information in the figure.

Solution:
In ∆MNP, seg NQ bisects ∠N. [Given]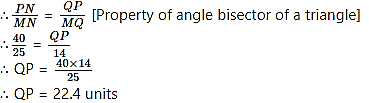

Question 7.
In the adjoining figure, if AB || CD || FE, then find x and AE.

Solution:
line AB || line CD || line FE [Given]

∴ X = 6 units
Now, AE AC + CE [A – C – E]
= 12 + x
= 12 + 6
= 18 units
∴ x = 6 units and AE = 18 units

Question 8.
In ∆LMN, ray MT bisects ∠LMN. If LM = 6, MN = 10, TN = 8, then find LT.

Solution:
In ∆LMN, ray MT bisects ∠LMN. [Given]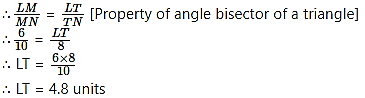

Question 9.
In ∆ABC,seg BD bisects ∠ABC. If AB = x,BC x+ 5, AD = x – 2, DC = x + 2, then find the value of x.

Solution:
In ∆ABC, seg BD bisects ∠ABC. [Given]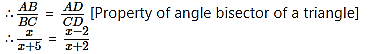

∴ x(x + 2) = (x – 2)(x + 5)
∴ x2 + 2x = x2 + 5x – 2x – 10
∴ 2x = 3x – 10
∴ 10 = 3x – 2x
∴ x = 10

Question 10.
In the adjoining figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.

Solution:

Question 11.
In ∆ABC, ray BD bisects ∠ABC and ray CE bisects ∠ACB. If seg AB = seg AC, then prove that ED || BC.

Solution:

Question 1.
i. Draw a ∆ABC.
ii. Bisect ∠B and name the point of intersection of AC and the angle bisector as D.
iii. Measure the sides.

iv. Find ratios  and 
v. You will find that both the ratios are almost equal.
vi. Bisect remaining angles of the triangle and find the ratios as above. Verify that the ratios are equal. (Textbook pg. no. 8)
Solution:

Note: Students should bisect the remaining angles and verify that the ratios are equal.

Question 2.
Write another proof of the above theorem (property of an angle bisector of a triangle). Use the following properties and write the proof.
i. The areas of two triangles of equal height are proportional to their bases.
ii. Every point on the bisector of an angle is equidistant from the sides of the angle. (Textbook pg. no. 9)

Given: In ∆CAB, ray AD bisects ∠A.

Construction: Draw seg DM ⊥ seg AB A – M – B and seg DN ⊥ seg AC, A – N – C.
Solution:
Proof:
In ∆ABC,
Point D is on angle bisector of ∠A. [Given]
∴DM = DN [Every point on the bisector of an angle is equidistant from the sides of the angle]

Question 3.
i. Draw three parallel lines.
ii. Label them as l, m, n.
iii. Draw transversals t₁ and t₂.
iv. AB and BC are intercepts on transversal t₁.
v. PQ and QR are intercepts on transversal t₂.
vi. Find ratios AB/BC and PQ/QR. You will find that they are almost equal. Verify that they are equal.(Textbook pg, no. 10)
Solution: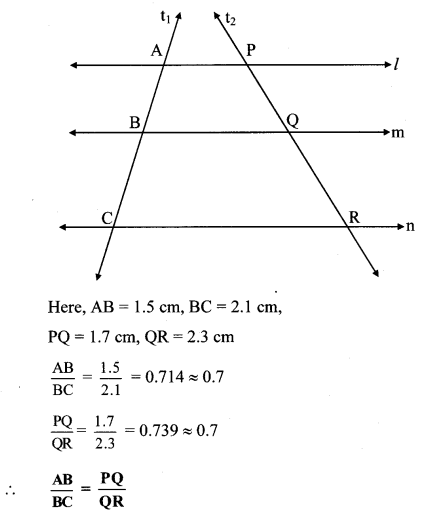

(Students should draw figures similar to the ones given and verify the properties.)

Question 4.
In the adjoining figure, AB || CD || EF. If AC = 5.4, CE = 9, BD = 7.5, then find DF. (Textbook pg, no. 12)

Solution:

Question 5.
In ∆ABC, ray BD bisects ∠ABC. A – D – C, side DE || side BC, A – E – B, then prove that AB/BC = AE/EB (Textbook pg, no. 13)

Solution: