Chapter 2 Pythagoras Theorem Set 2.1

Question 1.
Identify, with reason, which of the following are Pythagorean triplets.
i. (3,5,4)
ii. (4,9,12)
iii. (5,12,13)
iv. (24,70,74)
v. (10,24,27)
vi. (11,60,61)
Solution:
i. Here, 5² = 25
3² + 4² = 9 + 16 = 25
∴ 5² = 3² + 4²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (3,5,4) is a Pythagorean triplet.

ii. Here, 12² = 144
4² + 9²= 16 + 81 =97
∴ 12² ≠ 4² + 92
The square of the largest number is not equal to the sum of the squares of the other two numbers.
∴ (4,9,12) is not a Pythagorean triplet.

iii. Here, 13² = 169
5² + 12² = 25 + 144 = 169
∴ 13² = 5² + 12²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (5,12,13) is a Pythagorean triplet.

iv. Here, 74² = 5476
24² + 70² = 576 + 4900 = 5476
∴ 74² = 24² + 70²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (24, 70,74) is a Pythagorean triplet.

v. Here, 27² = 729
10² + 24² = 100 + 576 = 676
∴ 27² ≠ 10² + 24²
The square of the largest number is not equal to the sum of the squares of the other two numbers.
∴ (10,24,27) is not a Pythagorean triplet.

vi. Here, 61² = 3721
11² + 60² = 121 + 3600 = 3721
∴ 61² = 11² + 60²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (11,60,61) is a Pythagorean triplet.

Question 2.
In the adjoining figure, ∠MNP = 90°, seg NQ ⊥ seg MP,MQ = 9, QP = 4, find NQ.

Solution:

Question 3.
In the adjoining figure, ∠QPR = 90°, seg PM ⊥ seg QR and Q – M – R, PM = 10, QM = 8, find QR.

Solution:
In ∆PQR, ∠QPR = 90° and [Given]
seg PM ⊥ seg QR
∴ PM² = OM × MR [Theorem of geometric mean]
∴ 10² = 8 × MR
∴ MR = 100/8
= 12.5
Now, QR = QM + MR [Q – M – R]
= 8 + 12.5
∴ QR = 20.5 units

Question 4.
See adjoining figure. Find RP and PS using the information given in ∆PSR.

Solution:
In ∆PSR, ∠S = 90°, ∠P = 30° [Given]
∴ ∠R = 60° [Remaining angle of a triangle]
∴ ∆PSR is a 30° – 60° – 90° triangle.

Question 5.
For finding AB and BC with the help of information given in the adjoining figure, complete the following activity.

Solution:
AB = BC [Given]
∴ ∠BAC = ∠BCA [Isosceles triangle theorem]
Let ∠BAC = ∠BCA = x (i)
In ∆ABC, ∠A + ∠B + ∠C = 180° [Sum of the measures of the angles of a triangle is 180°]
∴ x + 90° + x = 180° [From (i)]
∴ 2x = 90°
∴ x = 90⁰ [From (i)]
∴ x = 45°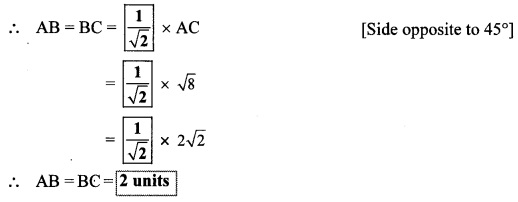

Question 6.
Find the side and perimeter of a square whose diagonal is 10 cm.

Solution:
Let ꠸ABCD be the given square.
l(diagonal AC) = 10 cm
Let the side of the square be ‘x’ cm.
In ∆ABC,
∠B = 90° [Angle of a square]
∴ AC² = AB² + BC² [Pythagoras theorem]
∴ 10² = x² + x²
∴ 100 = 2x²
∴ x² = 1002
∴x² = 50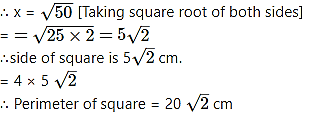

Question 7.
In the adjoining figure, ∠DFE = 90°, FG ⊥ ED. If GD = 8, FG = 12, find
i. EG
ii. FD, and
iii. EF

Solution:
i. In ∆DEF, ∠DFE = 90° and FG ⊥ ED [Given]
∴ FG² = GD × EG [Theorem of geometric mean]
∴ 122 = 8 × EG.
∴ EG = 144/8
∴ EG = 18 units

ii. In ∆FGD, ∠FGD = 90° [Given]
∴ FD² = FG² + GD² [Pythagoras theorem]
= 122 + 82 = 144 + 64
= 208

Question 8.
Find the diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.

Solution:
Let ꠸ABCD be the given rectangle.
AB = 12 cm, BC 35 cm
In ∆ABC, ∠B = 90° [Angle of a rectangle]
∴ AC² = AB² + BC² [Pythagoras theorem]
= 122 + 352
= 144 + 1225
= 1369

= 37 cm
∴ The diagonal of the rectangle is 37 cm.

Question 9.
In the adjoining figure, M is the midpoint of QR. ∠PRQ = 90°.
Prove that, PQ² = 4 PM² – 3 PR².

Solution:
Proof:
In ∆PQR, ∠PRQ = 90° [Given]
PQ² = PR² + QR² (i) [Pythagoras theorem]
RM = 12 QR [M is the midpoint of QR]
∴ 2RM = QR (ii)
∴ PQ² = PR² + (2RM)² [From (i) and (ii)]
∴ PQ² = PR² + 4RM² (iii)
Now, in ∆PRM, ∠PRM = 90° [Given]
∴ PM² = PR² + RM² [Pythagoras theorem]
∴ RM² = PM² – PR² (iv)
∴ PQ² = PR² + 4 (PM² – PR²) [From (iii) and (iv)]
∴ PQ² = PR² + 4 PM² – 4 PR²
∴ PQ² = 4 PM² – 3 PR²

Question 10.
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
Solution:
Let AC and CE represent the ladder of length 5.8 m, and A and E represent windows of the buildings on the opposite sides of the street. BD is the width of the street.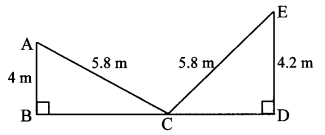

AB = 4 m and ED = 4.2 m
In ∆ABC, ∠B = 90° [Given]
AC² = AB² + BC² [Pythagoras theorem]
∴ 5.8² = 4² + BC²
∴ 5.8² – 4² = BC²
∴ (5.8 – 4) (5.8 + 4) = BC²
∴ 1.8 × 9.8 = BC²

CE² = CD² + DE² [Pythagoras theorem]
∴ 5.8² = CD² + 4.22
∴ 5.8² – 4.2² = CD²
∴ (5.8 – 4.2) (5.8 + 4.2) = CD²
∴ 1.6 × 10 = CD²
∴ CD² = 16
∴ CD = 4m (ii) [Taking square root of both sides]
Now, BD = BC + CD [B – C – D]
= 4.2 + 4 [From (i) and (ii)]
= 8.2 m
∴ The width of the street is 8.2 metres.

Question 1.
Verify that (3,4,5), (5,12,13), (8,15,17), (24,25,7) are Pythagorean triplets. (Textbook pg. no. 30)
Solution:
i. Here, 5² = 25
3² + 4² = 9 + 16 = 25
∴ 5² = 3² + 4²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 3,4,5 is a Pythagorean triplet.

ii. Here, 13² = 169
5² + 12² = 25 + 144 = 169
∴ 13² = 5² + 12²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 5,12,13 is a Pythagorean triplet.

iii. Here, 17² = 289
8² + 15² = 64 + 225 = 289
∴ 17² = 8² + 15²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 8,15,17 is a Pythagorean triplet.

iv. Here, 25² = 625
7² + 24² = 49 + 576 = 625
∴ 25² = 7² + 24²
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 24,25, 7 is a Pythagorean triplet.

Question 2.
Assign different values to a and b and obtain 5 Pythagorean triplets. (Textbook pg. no. 31)
Solution:
i. Let a = 2, b = 1
a² + b² = 2² + 1² = 4 + 1 = 5
a² – b² = 2² – 1² = 4 – 1 = 3
2ab = 2 × 2 × 1 = 4
∴ (5, 3, 4) is a Pythagorean triplet.

ii. Let a = 4,b = 3
a² + b² = 4² + 3² = 16 + 9 = 25
a² – b² = 4² – 3² = 16 – 9 = 7
2ab = 2 × 4 × 3 = 24
∴ (25, 7, 24) is a Pythagorean triplet.

iii. Let a = 5, b = 2
a² + b² = 5² + 2² = 25 + 4 = 29
a² – b² = 5² – 2² = 25 – 4 = 21
2ab = 2 × 5 × 2 = 20
∴ (29, 21, 20) is a Pythagorean triplet.

iv. Let a = 4,b = 1
a² + b² = 4² + 1² = 16 + 1 = 17
a² – b² = 42 – 12 = 16 – 1 = 15
2ab = 2 × 4 × 1 = 8
∴ (17, 15, 8) is a Pythagorean triplet.

v. Let a = 9, b = 7
a² + b² = 92 + 72 = 81 + 49 = 130
a² – b² = 92 – 72 = 81 – 49 = 32
2ab = 2 × 9 × 7 = 126
∴ (130,32,126) is a Pythagorean triplet.

Note: Numbers in Pythagorean triplet can be written in any order.