Chapter 2 Quadratic Equations Set 2.2

Question 1.
Solve the following quadratic equations by factorisation.
i. x² – 15x + 54 = 0
ii. x² + x – 20 = 0
iii. 2y² + 27y + 13 = 0
iv. 5m² = 22m + 15

vii. √2x² + 7x + 5√2 = 0 to solve this quadratic equation by factorisation complete the following activity
viii. 3x² – 2√6x + 2 = 0
ix. 2m(m – 24) = 50
x. 252 = 9
xi. 7m² = 21 m
xii. m² – 11 = 0
Solution:

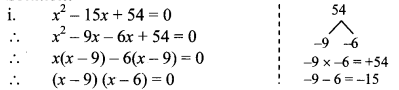
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x – 9 = 0 or x – 6 = 0
∴ x = 9 or x = 6
∴ The roots of the given quadratic equation are 9 and 6.

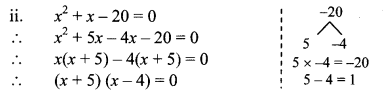
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 5 = 0 or x – 4 = 0
∴ x = -5 or x = 4
∴ The roots of the given quadratic equation are -5 and 4.

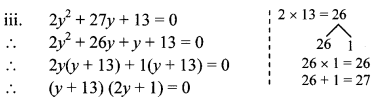
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get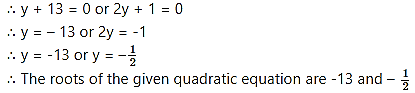

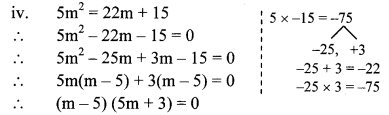
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get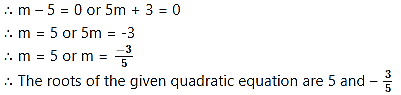

By using the property, if the product of two numbers is zero, then at least one of them is zero, we get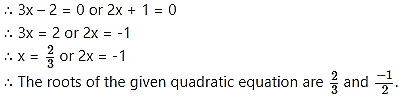

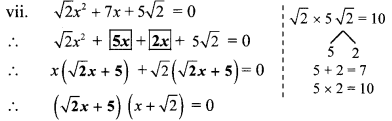
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get

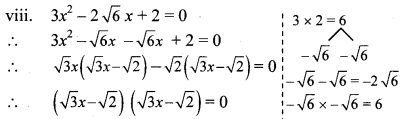
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get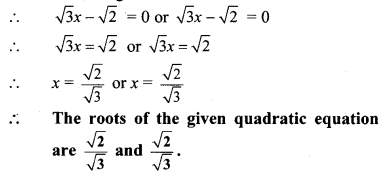

ix. 2m (m – 24) = 50
∴ 2m² – 48m = 50
∴ 2m² – 48m – 50 = 0
∴m² – 24m – 25 = 0 …[Dividing both sides by 2]

∴ m – 25 = 0 or m + 1 = 0
∴ m = 25 or m = -1
∴ The roots of thes given quadratic equation are 25 and -1.

x. 25m² = 9
∴ 25m² – 9 = 0
∴ (5m)² – (3)² = 0
∴ (5m + 3) (5m – 3) = 0
…. [∵a² – b² = (a + b) (a – b)]
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get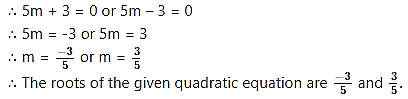

xi. 7m² = 21m
∴ 7m² – 21m = 0
∴ m² – 3m = 0 …[Dividing both sides by 7]
∴ m(m – 3) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ m = 0 or m – 3 = 0
∴ m = 0 or m = 3
∴ The roots of the given quadratic equation are 0 and 3.

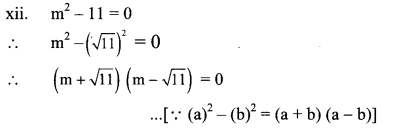
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ m + √11 = 0 or m – √11 = 0
∴ m = -√11 or m = √11
∴ The roots of the given quadratic equation are – √11 and √11