Chapter 3 Arithmetic Progression Set 3.3

Question 1.
First term and common difference of an A.P. are 6 and 3 respectively; find S₂₇.
Solution:

Question 2.
Find the sum of first 123 even natural numbers.
Solution:
The even natural numbers are 2, 4, 6, 8,…
The above sequence is an A.P.
∴ a = 2, d = 4 – 2 = 2, n = 123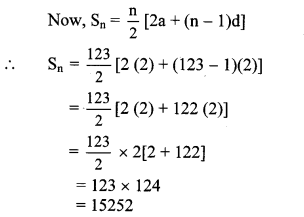

∴ The sum of first 123 even natural numbers is 15252.

Question 3.
Find the sum of all even numbers between 1 and 350.
Solution:
The even numbers between 1 and 350 are 2, 4, 6,…, 348.
The above sequence is an A.P.
∴ a = 2, d = 4 – 2 = 2, t_n = 348
Since, t_n = a + (n – 1)d
∴ 348 = 2 + (n – 1)2
∴ 348 – 2 = (n – 1)2
∴ 346 = (n – 1)2

= 87(4 + 173 × 2)
= 87(4 + 346)
= 87 × 350
∴ S₁₇₄ = 30450
∴ The sum of all even numbers between 1 and 350 is 30450.

Question 4.
In an A.P. 19^th term is 52 and 38^th term is 128, find sum of first 56 terms.
Solution:
For an A.P., let a be the first term and d be the common difference.
t₁₉ = 52, t₃₈ = 128 …[Given]
Since, t_n = a + (n – 1)d
∴ t₁₉ = a + (19 – 1)d
∴ 52 = a + 18d
i.e. a + 18d = 52 …(i)
Also, t₃₈ = a + (38 – 1)d
∴ 128 = a + 37d
i.e. a + 37d = 128 …(ii)
Adding equations (i) and (ii), we get

Question 5.
Complete the following activity to find the sum of natural numbers between 1 to 140 which are divisible by 4.
Solution: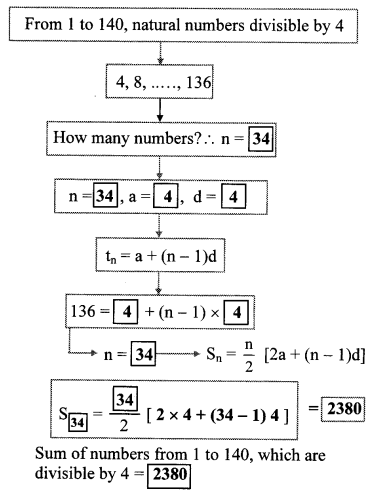

Question 6.
Sum of first 55 terms in an A.P. is 3300, find its 28^th term.
Solution:
For an A.P., let a be the first term and d be the common difference.
S₅₅ =3300 …[Given]

Question 7.
In an A.P. sum of three consecutive terms is 27 and their product is 504, find the terms. (Assume that three consecutive terms in A.P. are a – d, a, a + d.)
Solution:
Let the three consecutive terms in an A.P. be
a – d, a and a + d.
According to the first condition,
a – d + a + a + d = 27
∴ 3a = 27
∴ a =   
∴ a = 9 ….(i)
According to the second condition,
(a – d) a (a + d) = 504
∴ a(a² – d²) = 504
∴ 9(a² – d²) = 504 …[From (i)]
∴ 9(81 – d²) = 504
∴ 81 – d² = 5049
∴ 81 – d² = 56
∴ d² = 81 – 56
∴ d² = 25
Taking square root of both sides, we get
d = ± 5
When d = 5 and a =9,
a – d 9 – 5 = 4
a = 9
a + d 9 + 5 = 14
When d = -5 and a = 9,
a – d = 9 – (-5) = 9 + 5 = 14
a = 9
a + d = 9 – 5 = 4
∴ The three consecutive terms are 4, 9 and 14 or 14, 9 and 4.

Question 8.
Find four consecutive terms in an A.P. whose sum is 12 and sum of 3^rd and 4^th term is 14. (Assume the four consecutive terms in A.P. are a – d, a, a + d, a + 2d.)
Solution:
Let the four consecutive terms in an A.P. be
a – d, a, a + d and a + 2d.
According to the first condition,
a – d + a + a + d + a + 2d = 12
∴ 4a + 2d =12
∴ 2(2a + d) = 12
∴ 2a + d = 122
∴ 2a + d = 6 …(i)
According to the second condition,
a + d + a + 2d = 14
∴ 2a + 3d = 14 …(ii)
Subtracting equation (i) from (ii), we get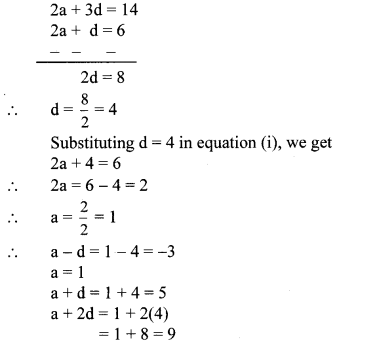

∴ The four consecutive terms are -3,1,5 and 9.

Question 9.
If the 9^th term of an A.P. is zero, then show that the 29^th term is twice the 19th term.
To prove: t₂₉ = 2t₁₉
Proof:
For an A.P., let a be the first term and d be the common difference.
t₉ = 0 …[Given]
Since, tn = a + (n – 1)d
∴ t₉ = a + (9 – 1)d
∴ 0 = a + 8d
∴ a = -8d …(i)
Also, t₁₉ = a + (19 – 1)d
= a + 18d
= -8d + 18d … [From (i)]
∴ t₁₉ = 10d …(ii)
and t₂₉ = a + (29 – 1)d
= a + 28d
= -8d + 28d …[From (i)]
∴ t₂₉ = 20d = 2(10d)
∴ t₂₉ = 2(t₁₉) … [From (ii)]
∴ The 29^th term is twice the 19th term.

Question 1.
Find the sum of all odd numbers from 1 to 150. (Textbook pg, no. 71)
Solution:
Odd numbers from 1 to 150 are 1,3, 5, 7,…, 149
Here, difference between any two consecutive terms is 2.
∴ It is an A.P.
∴ a = 1, d = 2
Let us find how many odd numbers are there from 1 to 150, i.e. find the value of n if
t_n = 149
t_n = a + (n – 1)d
∴ 149 = 1 + (n – 1)2
∴ 149 – 1 = (n – 1)2
∴  = n – 1
∴ 74 = n – 1
∴ n = 74 + 1 = 75

ii. Now, let’s find the sum of 75 numbers
i. e. 1 + 3 + 5 + 7 + … + 149