Question 1.
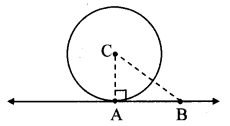
In the adjoining figure, the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
i. What is the measure of ∠CAB? Why?
ii. What is the distance of point C from line AB? Why?
iii. d(A, B) = 6 cm, find d(B, C).
iv. What is the measure of ∠ABC? Why?
Solution:
i. line AB is the tangent to the circle with centre C and radius AC. [Given]
∴ ∠CAB = 90° (i) [Tangent theorem]
ii. seg CA ⊥ line AB [From (i)]
radius = l(AC) = 6 cm
∴ The distance of point C from line AB is 6 cm.
iii. In ∆CAB, ∠CAB = 90° [From (i)]
∴ BC2 = AB2 + AC2 . [Pythagoras theorem]
= 62 + 62
= 2 × 62
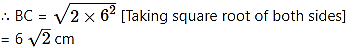
∴ d(B, C) = 6 cm
iv. In ∆ABC,
AC = AB = 6cm
∴ ∠ABC = ∠ACB [Isosceles triangle theorem]
Let ∠ABC = ∠ACB =x
In ∆ABC,
∠CAB + ∠ABC + ∠ACB = 180° [Sum of the measures of angles of a triangle is 180°]
∴ 90° + x + x = 180°
∴ 90 + 2x = 180°
∴ 2x = 180°- 90°
∴ x = 900/2
∴ x = 45°
∴ ∠ABC = 45°
Question 2.
In the adjoining figure, O is the centre of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm, then
i. What is the length of each tangent segment?
ii. What is the measure of ∠MRO?
iii. What is the measure of ∠MRN?
Solution:
seg RM and seg RN are tangents to the circle with centre O. [Given]
∴ ∠OMR = ∠ONR = 90° [Tangent theorem]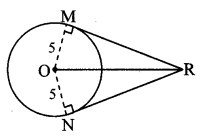
i. In ∆OMR, ∠OMR = 90°
∴ OR2 = OM2 + RM2 [Pythagoras theorem]
∴ 102 = 52 + RM2
∴ 100 = 25 + RM2
∴ RM2 = 75![]()
∴ RM = RN [Tangent segment theorem]
Length of each tangent segment is 5√3 cm.
ii. In ∆RMO,
∠OMR = 90° [Tangent theorem]
OM = 5 cm and OR = 10 cm
∴ OM = 1/2 OR
∴ ∠MRO = 30° (i) [Converse of 30° – 60° – 90° theorem]
Similarly, ∠NRO = 30°
iii. But, ∠MRN = ∠MRO + ∠NRO [Angle addition property]
= 30° + 30° [From (i)]
∴ ∠MRN = 60°
Question 3.
Seg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON.
Solution:
Proof:
In ∆OMR and ∆ONR,
seg RM ≅ seg RN [Tangent segment theorem]
seg OM ≅ seg ON [Radii of the same circle]
seg OR ≅ seg OR [Common side]
∴ ∆OMR ≅ ∆ONR [SSS test of congruency]
{∴ ∠MRO ≅ ∠NRO
∠MOR ≅ ∠NOR } [c.a.c.t.]
∴ seg OR bisects ∠MRN and ∠MON.
Question 4.
What is the distance between two parallel tangents of a circle having radius 4.5 cm? Justify your answer.
Solution:
Let the lines PQ and RS be the two parallel tangents to circle at M and N respectively. Through centre O, draw line AB || line RS.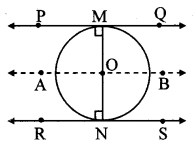
OM = ON = 4.5 [Given]
line AB || line RS [Construction]
line PQ || line RS [Given]
∴ line AB || line PQ || line RS
Now, ∠OMP = ∠ONR = 90° (i) [Tangent theorem]
For line PQ || line AB,
∠OMP = ∠AON = 90° (ii) [Corresponding angles and from (i)]
For line RS || line AB,
∠ONR = ∠AOM = 90° (iii) [Corresponding angles and from (i)]
∠AON + ∠AOM = 90° + 90° [From (ii) and (iii)]
∴ ∠AON + ∠AOM = 180°
∴ ∠AON and ∠AOM form a linear pair.
∴ ray OM and ray ON are opposite rays.
∴ Points M, O, N are collinear. (iv)
∴ MN = OM + ON [M – O – N, From (iv)]
∴ MN = 4.5 + 4.5
∴ MN = 9 cm
∴ Distance between two parallel tangents PQ and RS is 9 cm.
Question 1.
In the adjoining figure, seg QR is a chord of the circle with centre O. P is the midpoint of the chord QR. If QR = 24, OP = 10, find radius of the circle. To find solution of the problem, write the theorems that are useful. Using them, solve the problem. (Textbook pg. no. 48)
Solution:
Theorems which are useful to find solution:
i. The segment joining the centre of a circle and the midpoint of a chord is perpendicular to the chord.
ii. In a right angled triangle, sum of the squares of the perpendicular sides is equal to square of its hypotenuse.
QP = 1/2 (QR) [P is the midpoint of chord QR]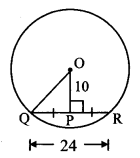
1/2 × 24 = 12 units
Also, seg OP ⊥ chord QR [The segment joining centre of a circle and midpoint of a chord is perpendicular to the chord]
In ∆OPQ, ∠OPQ = 90°
∴ OQ2 = OP2 + QP2 [Pythagoras theorem]
= 102 + 122
= 100 + 144
= 244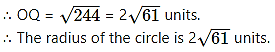
Question 2.
In the adjoining figure, M is the centre of the circle and seg AB is a diameter, seg MS ⊥ chord AD, seg MT ⊥ chord AC, ∠DAB ≅ ∠CAB.
i. Prove that: chord AD ≅ chord AC.
ii. To solve this problem which theorems will you use?
a. The chords which are equidistant from the centre are equal in length.
b. Congruent chords of a circle are equidistant from the centre.
iii. Which of the following tests of congruence of triangles will be useful?
a. SAS b. ASA c. SSS d. AAS e. Hypotenuse-side test.
Using appropriate test and theorem write the proof of the above example. (Textbook pg. no, 48)
Solution:
Proof:
i. ∠DAB ≅ ∠CAB [Given]
∴ ∠SAM ≅ ∠TAM (i) [A – S – D, A – M – B, A -T – C]
In ∆SAM and ∆TAM,
∠SAM ≅ ∠TAM [From (i)]
∠ASM ≅ ∠ATM [Each angle is of measure 90°]
seg AM ≅ seg AM [Common side]
∴ ∆SAM ≅ ∆TAM [AAS [SAA] test of congruency]
∴ side MS ≅ side MT [c.s.c.t]
But, seg MS ⊥ chord AD [Given]
seg MT ⊥chord AC
∴ chord AD ≅ chord AC [Chords of a circle equidistant from the centre are congruent]
ii. Theorem used for solving the problem:
The chords which are equidistant from the centre are equal in length.
iii. Test of congruency useful in solving the above problem is AAS ISAAI test of congruency.
Question 3.
i. Draw segment AB. Draw perpendicular bisector l of the segment AB. Take point P on the line l as centre,
PA as radius and draw a circle. Observe that the circle passes through point B also. Find the reason.
ii. Taking any other point Q on the line l, if a circle is drawn with centre Q and radius QA, will it pass through B? Think.
iii. How many such circles can be drawn, passing through A and B? Where will their centres lie? (Textbook pg. no. 49)
Solution: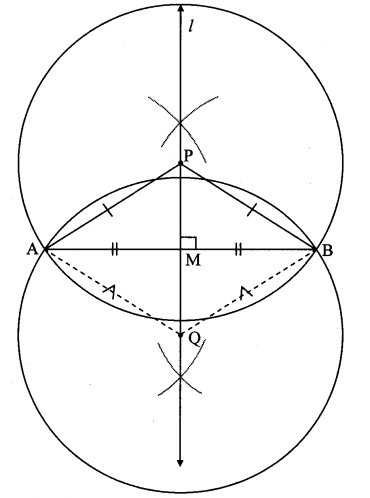
i. Draw the circle with centre P and radius PA.
line l is the perpendicular bisector of seg AB.
Every point on the perpendicular bisector of a segment is equidistant from the endpoints of the segment.
∴ PA = PB … [Perpendicular bisector theorem]
∴ PA = PB = radius
∴ The circle with centre P and radius PA passes through point B.
ii. The circle with any other point Q and radius QA is drawn.
QA = QB = radius … [Perpendicular bisector theorem]
∴ The circle with centre Q and radius QA passes through point B.
iii. We can draw infinite number of circles passing through A and B.
All their centres will lie on the perpendicular bisector of AB (i.e., line l)
Question 4.
i. Take any three non-collinear points. What should be done to draw a circle passing through all these points? Draw a circle through these points.
ii. Is it possible to draw one more circle passing through these three points? Think of it. (Textbook pg. no. 49)
Solution:
i. Let points A, B, C be any three non collinear points.
Draw the perpendicular bisector of seg AB (line l).
∴ Points A and B are equidistant from any point of line l ….(i)[Perpendicular bisector theorem]
Draw the perpendicular bisector of seg BC (line m) to intersect line l at point P.
∴ Points B and C are equidistant from any point of line m ….(ii) [Perpendicular bisector theorem]
∴ PA = PB …[From (i)]
PB = PC … [From (ii)]
∴ PA = PB = PC = radius
∴ With PA as radius the required circle is drawn through points A, B, C.
ii. It is not possible to draw more than one circle passing through these three points.
Question 5.
Take 3 collinear points D, E, F. Try to draw a circle passing through these points. If you are not able to draw a circle, think of the reason. (Textbook pg. no. 49)
Solution:
Let D, E, F be the collinear points.
The perpendicular bisector of DE and EF drawn (i.e., line l and line m) do not intersect at a common point.
∴ There is no single common point (centre of circle) from which a circle can be drawn passing through points D, E and F.
Hence, we cannot draw a circle passing through points D, E and F.
Question 6.
Which theorem do we use in proving that hypotenuse is the longest side of a right angled triangle? (Textbook pg. no. 52)
Solution:
In ∆ABC,
∠ABC = 90°
∴ ∠BAC < 90° and ∠ACB < 90° [Given]
∴ ∠ABC > ∠BAC and ∠ABC > ∠ACB
∴ AC > BC and AC > AB [Side opposite to greater angle is greater]
∴ Hypotenuse is the longest side in right angled triangle.
We use theorem, If two angles of a triangle are not equal, then the side opposite to the greater angle is greater than the side opposite to the smaller angle.
Question 7.
Theorem: Tangent segments drawn from an external point to a circle are congruent
Draw radius AP and radius AQ and complete the following proof of the theorem.
Given: A is the centre of the circle.
Tangents through external point D touch the circle at the points P and Q.
To prove: seg DP ≅ seg DQ
Construction: Draw seg AP and seg AQ.
Solution:
Proof:
In ∆PAD and ∆QAD,
seg PA ≅ [segQA] [Radii of the same circle]
seg AD ≅ seg AD [Common side]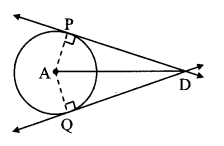
∠APD = ∠AQD = 90° [Tangent theorem]
∴ ∆PAD = ∆QAD [By Hypotenuse side test]
∴ seg DP = seg DQ [c.s.c.t]
