Question 1.
In the adjoining figure, points G, D, E, F are concyclic points of a circle with centre C.
∠ECF = 70°, m(arc DGF) = 200°. Find m(arc DE) and m(arc DEF).
Solution:
m(arc EF) = m∠ECF [Definition of measure of minor arc]
∴ m(arc EF) = 70°
i. m(arc DE) + m(arc DGF)
+ m(arc EF) = 360° [Measure of a circle is 360°]
∴ m(arc DE) = 360° – m(arc DGF) – m(arc EF)
= 360° – 200° – 70°
∴ m(arc DE) = 90°
ii. m(arc DEF) = m(arc DE) + m(arc EF) [Arc addition property]
= 90° + 70°
∴ m(arc DEF) = 160°
Question 2.
In the adjoining figure, AQRS is an equilateral triangle. Prove that,
i. arc RS ≅ arc QS ≅ arc QR
ii. m(arc QRS) = 240°.
Solution:
Proof:
i. ∆QRS is an equilateral triangle, [Given]
∴ seg RS ≅ seg QS ≅ seg QR [Sides of an equilateral triangle]
∴ arc RS ≅ arc QS ≅ arc QR [Corresponding arcs of congruents chords of a circle are congruent]
ii. Let m(arc RS) = m(arc QS)= m(arc QR) = x
m(arc RS) + m(arc QS) + m(arc QR) = 360° [Measure of a circle is 360°, arc addition property]
∴ x + x + x = 360°
∴ 3x = 360°
∴ x =360°/3 =120∘
∴ m(arc RS) = m(arc QS) = m(arc QR) = 120° (i)
Now, m(arc QRS) = m(arc QR) + m(arc RS) [Arc addition property]
= 120° + 120° [From (i)]
∴ m(arc QRS) = 240°
Question 3.
In the adjoining figure, chord AB ≅ chord CD. Prove that, arc AC = arc BD.
Solution:
Proof:
chord AB ≅ chord CD [Given]
∴ arc AB ≅ arc CD [Corresponding arcs of congruents chords of a circle are congruent]
∴ m(arc AB) = m(arc CD)
∴ m(arc AC) + m(arc BC) = m(arc BC) + m(arc BD) [Arc addition property]
∴ m(arc AC) = m(arc BD)
∴ arc AC ≅ arc BD
Intext Questions and Activities
Question 1.
Theorem : The chords corresponding to congruent arcs of a circle (or congruent circles) are congruent. (Textbook pg. no. 61)
Given: B is the centre of circle.
arc APC ≅ arc DQE
To prove: chord AC ≅ chord DE
Proof:
[m(arc APC) = ∠ABC (i) [Definition of measure of
m(arc DQE) = ∠DBE] (ii) minor arc]
arc APC ≅ arc ∠DQE (iii) [Given]
∴ ∠ABC ≅ ∠DBE [From (i), (ii) and (iii)]
In ∆ABC and ∆DBE,
side AB ≅ side DB [Radil of the same circle]
side [CB] side [EB] [Radii of the same circle]
∠ABC ≅∠DBE [From (iii), Measures of congruent arcs]
∴ ∆ABC ≅ ∆DBE [SAS test of congruency]
∴ chord AC ≅ chord DE [c.s.c.t]
Question 2.
Theorem: Corresponding arcs of congruent chords of a circle (or congruent circles) are congruent (Textbook pg. no. 61)
Given: O is the centre of circle, chord PQ = chord RS
To prove: arc PMQ = arc RNS
Proof:
In ∆POQ and ∆ROS,
[side PO ≅ side RO
side OQ ≅ side OS] [Radii of the same circle]
chord PQ ≅ chord RS [Given]
∴ ∆POQ ≅ ∆ROS [SSS test of congruency]
∴ ∠POQ ≅ ∠ROS (i) [c.a.c.t.]
m(arc PMQ) = ∠POQ (ii)
m(arc RNS) = ∠ROS (iii) [Definition of measure of minor arc]
∴ arc PMQ ≅ arc RNS [From (i), (ii) and (iii)]
Question 3.
Prove the two theorems on textbook pg.no.61 for congruent circles. (Textbook pg. no. 62)
Theorem : The chords corresponding to congruent arcs of congruent circles are congruent
Given: In congruent circles with centres B and R,
arc APC ≅ arc DQE
To prove: chord AC ≅ chord DE
Proof:
[m(arc APC) = ∠ABC (i)
m(arc DQE) = ∠DRE] (ii) [Definition of measure of minor arc]
arc APC ≅ arc DQE (iii) [Given]
∴ ∠ABC = ∠DRE (iv) [From (i), (ii) and (iii)]
In ∆ABC and ∆DRE,
[side AB ≅ side DR [Radii of congruent circles]
side CB ≅ side ER] [From (iv)]
∠ABC ≅ ∠DRE
∴ ∆ABC ≅ ∆DRE [SAS test of congruency]
Question 4.
While proving the first theorem of the two, we assume that the minor arc APC and minor arc DQE are congruent. Can you prove the same theorem by assuming that corresponding major arcs congruent? (Textbook pg. no. 62)
Statement:
The chords corresponding to congruent major arcs of a circle are congruent.
Given: B is the centre of circle.
arc AXC ≅ arc DXE
To prove: chord AC ≅ chord DE
Proof:
m(major arc) = 360° – m(minor arc)
∴ m(arc AXC) = 360° – m(arc APC) (i)
m(arc DXE) = 360° – m(arc DQE) (ii)
m(arc AXC) = m(arc DXE) (iii) [Given]
∴ 360° – m(arc APC) = 360°- m(arc DQE) [From (i), (ii) and (iii)]
∴ m(arc APC) = m(arc DQE) (iv)
∴ m(arc APC) = ∠ABC (v) [Definition of measure of minor arc]
m(arc DQE) = ∠DBE (vi)
∴ ∠ABC = ∠DBE (vii) [From (iv), (v) and (vi)]
In ∆ABC and ∆DBE,
[side AB ≅ side DB
Side CB ≅ side EB] [Radii of the same circle]
∠ABC ≅ ∠DBE [From (vii)]
∴ ∆ABC ≅ ∆DBE [SAS test of congruency]
∴ chord AC ≅ chord DE [c.s.c.t.]
Question 5.
i. In the second theorem, are the major arcs corresponding to congruent chords congruent?
ii. Is the theorem true, when the chord PQ and chord RS are diameters of the circle? (Textbook pg. no. 62)
Solution:
i. Yes, the major arcs corresponding to congruent chords are congruent.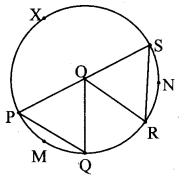
Proof:
In ∆POQ and ∆ROS,
seg OP ≅ seg OR [Radii of the same circle]
seg OQ ≅ seg OS [Radii of the same circle]
seg PQ ≅ seg RS [Given]
∴ ∆POQ ≅ ∆ROS [SSS test of congruence]
∴ ∠POQ ≅ ∠SOR (i) [c.a.c.t]
[ m(arc PMQ) = ∠POQ (ii)
m(arc RNS) = ∠SOR ] (iii) [Definition of measure of minor arc]
∴ m(arc PMQ) = m(arc RNS)
m(minor arc) = 360° – m(major arc) (iv) [From (i), (ii) and (iii)]
m(arc PMQ) = 360° – m(arc PXQ) (v)
and m(arc RNS) = 360° – m(arc RXS) (vi)
∴ 360°- m(arc PXQ) = 360°- m(arc RXS) [From (iv), (v) and (vi)]
∴ m(arc PXQ) = m(arc RXS)
ii. Yes, the major arcs corresponding to congruent chords (diameters) are congruent.
Given: O is the centre of circle.
seg PQ and seg RS are the diameters.
To prove: arc PYQ ≅ arc RYS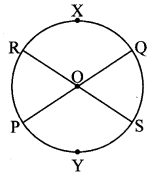
Proof:
seg PQ and seg RS are the diameters of the same circle. [Given]
∴ arc PYQ and arc RYS are semicircular arcs.
∴ m(arc PYQ) = m(arc RYS) = 180° [Measure of a semicircular arc is 180°]
∴ arc PYQ ≅ arc RYS
