Chapter 3 Indefinite Integration Ex 3.3

I. Evaluate the following:

Question 1.
∫ log x dx
Solution: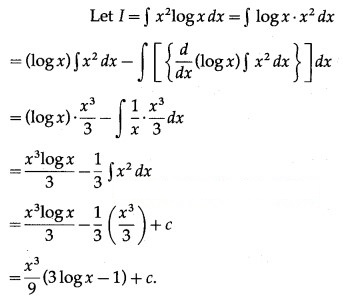

Question 2.
∫ sin 3x dx
Solution: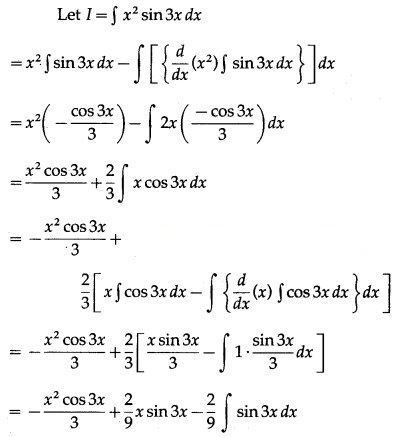

Question 3.
∫x  x dx
Solution: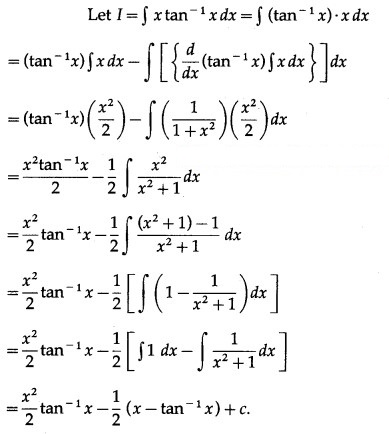

Question 4.
∫  x dx
Solution:

Question 5.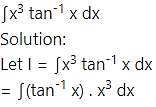

Question 6.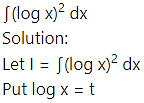

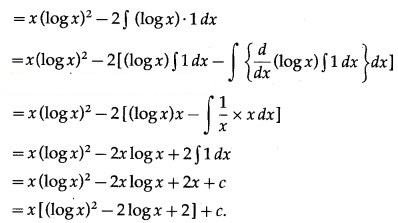
Question 7.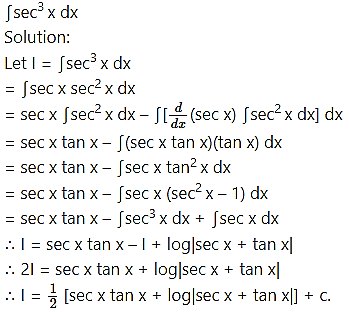

Question 8.
∫x . x dx
Solution: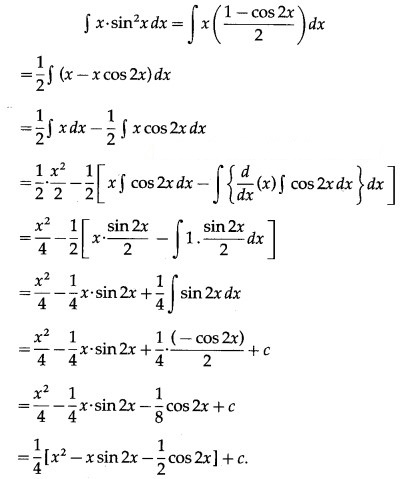

Question 9.
∫ log x dx
Solution: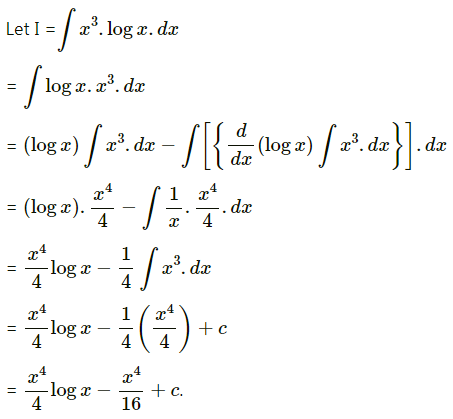

Question 10.
∫ cos 3x dx
Solution: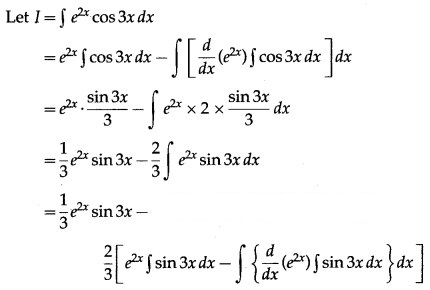

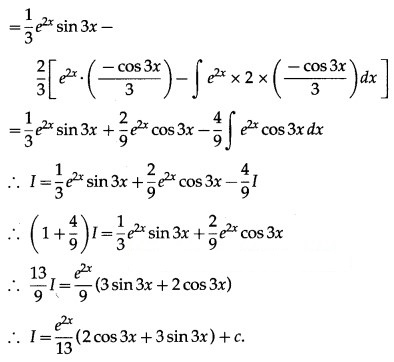
Question 11.
∫x  x dx
Solution:

Question 12.
∫  x dx
Solution: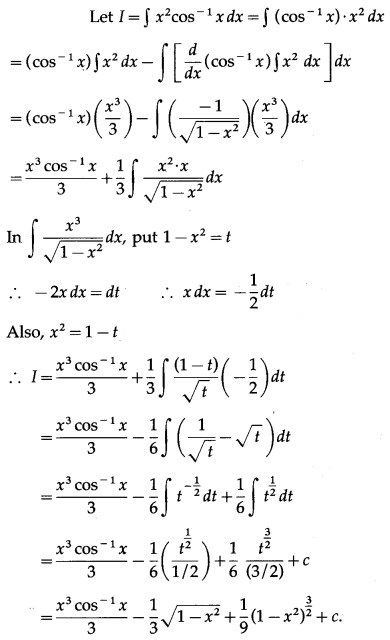

Question 13.

Solution:

= t(log t – 1) + c
= (log x) . [log(log x) – 1] + c.

Question 14.

Solution: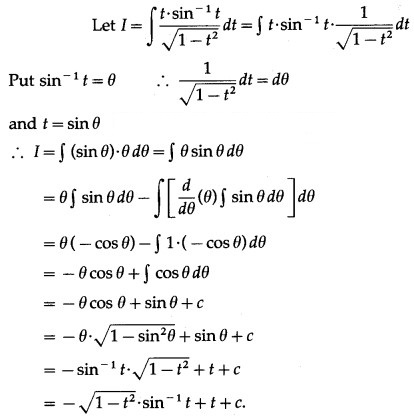

Question 15.

Question 16.
∫sin θ . log(cos θ) dθ
Solution:
Let I = ∫sin θ . log (cos θ) dθ
= ∫log(cos θ) . sin θ dθ
Put cos θ = t
∴ -sin θ dθ = dt
∴ sin θ dθ = -dt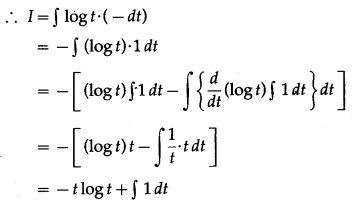

= -t log t + t + c
= -cos θ . log(cos θ) + cos θ + c
= -cos θ [log(cos θ) – 1] + c.

Question 17.

Question 18.

Solution:

Question 19.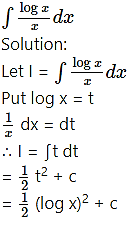

Question 20.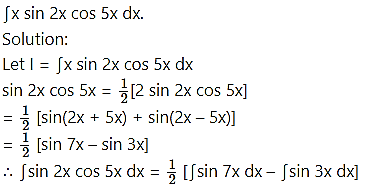

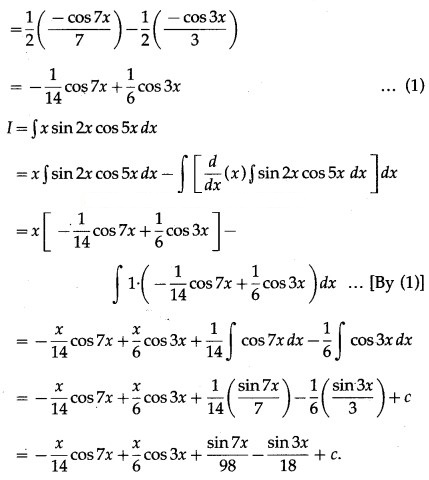
Question 21.

II. Integrate the following functions w.r.t. x:

Question 1.
 sin 3x
Solution:

Question 2.
cos 2x
Solution:

Question 3.
sin(log x)
Solution: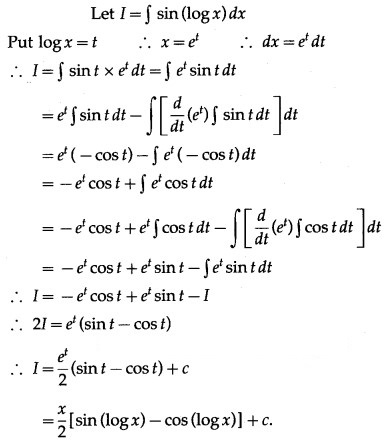

Question 4.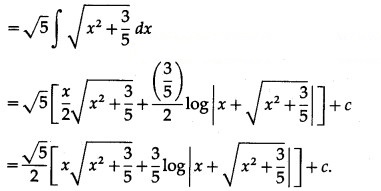

Question 5.

Solution: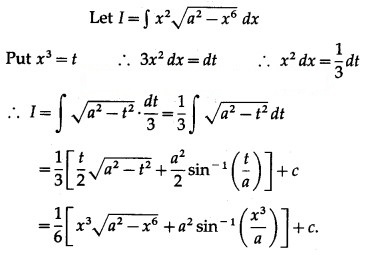

Question 6.

Solution: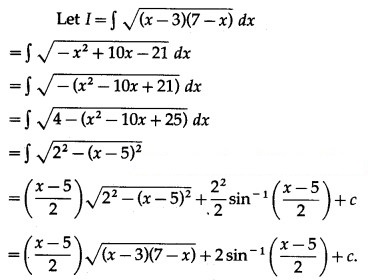

Question 7.

Solution:

Question 8.

Question 9.

= A[-4 – 2x] + B
= -2Ax + (B – 4A)
Comparing the coefficients of x and the constant term on both sides, we get
-2A = 1, B – 4A = 0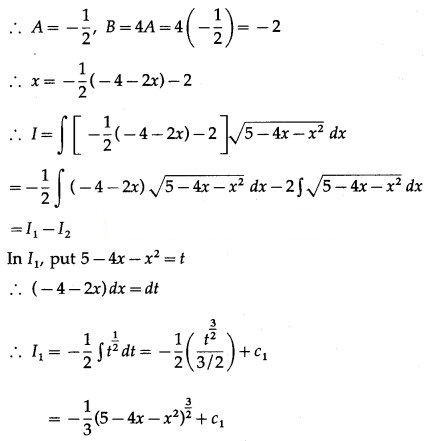

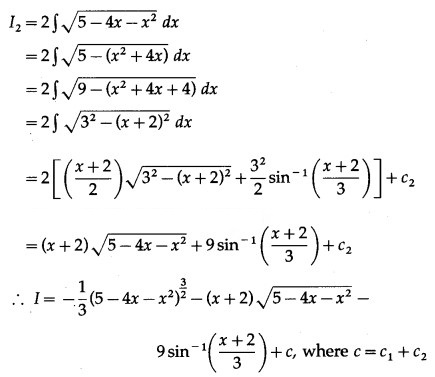
Question 10.

Solution: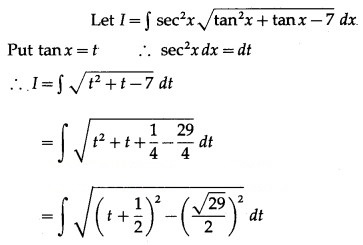

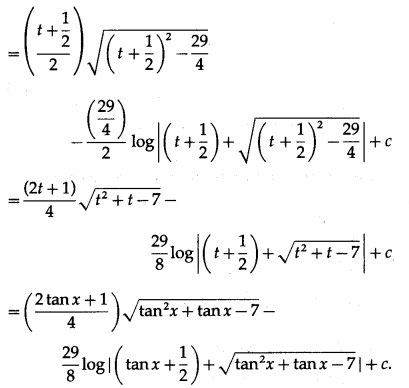
Question 11.

Solution: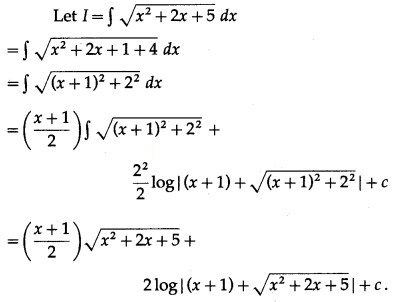

Question 12.

Solution: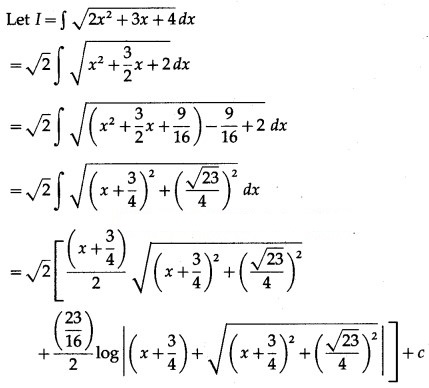

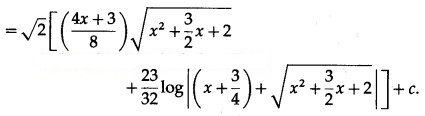
III. Integrate the following functions w.r.t. x:

Question 1.

Question 2.

Solution:

Question 3.

Question 4.

Solution: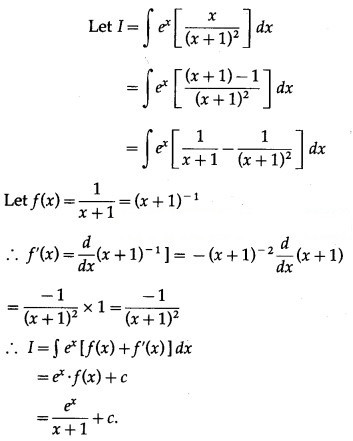

Question 5.

Solution: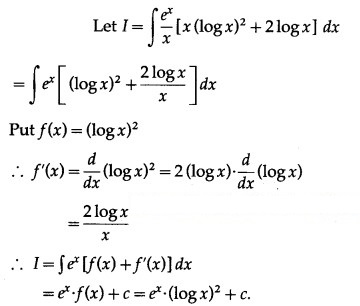

Question 6.

Question 7.

Solution: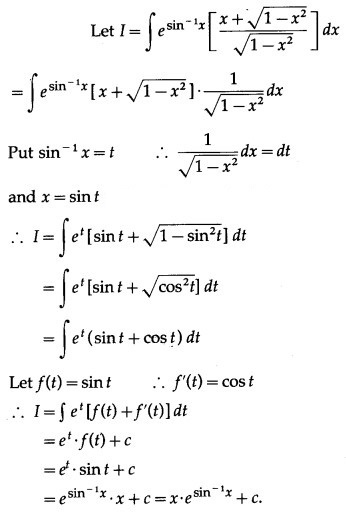

Question 8.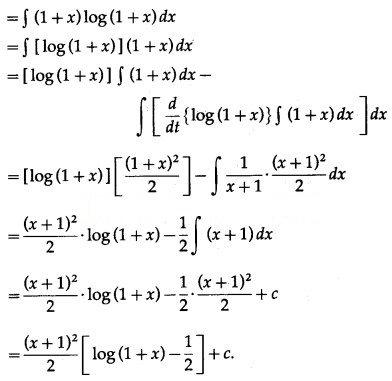

Question 9.