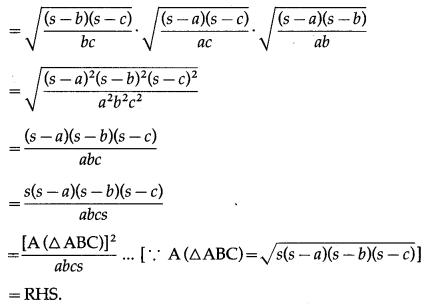Chapter 3 Trigonometric Functions Ex 3.2

Question 1.
Find the Cartesian co-ordinates of the point whose polar co-ordinates are :

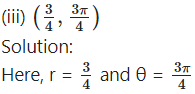
Let the cartesian coordinates be (x, y)

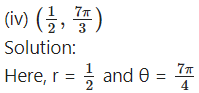
Let the cartesian coordinates be (x, y)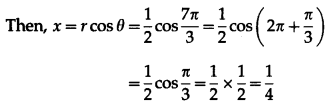

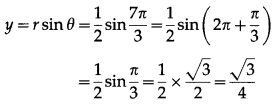
Question 2.
Find the of the polar co-ordinates point whose Cartesian co-ordinates are.

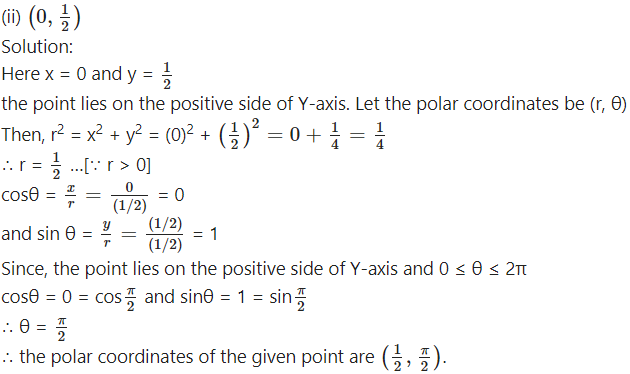
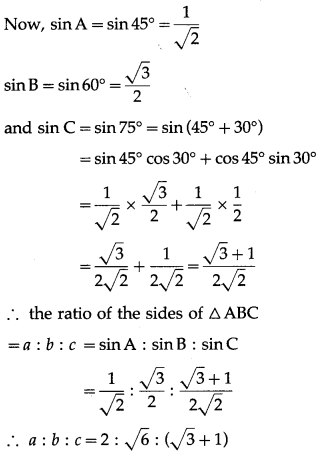
Question 4.

Solution:
By the sine rule,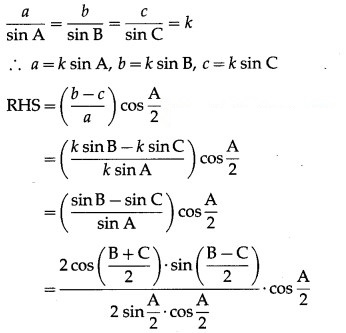

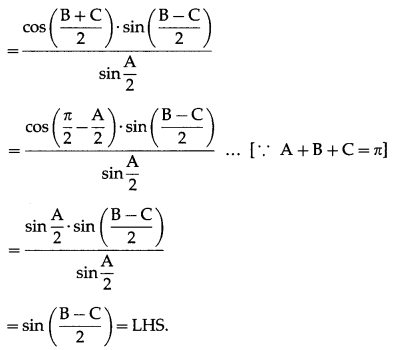
Question 5.

Solution:

Question 6.
In ∆ABC, prove that a³sin(B – C) + b³sin(C – A) + c³sin(A – B) = 0
Solution:
By the sine rule,

∴ a = k sin A, b = k sin B, c = k sin C
LHS = a³sin (B – C) + b³sin (C – A) + c³sin (A – B)
= a³(sin B cos C – cos B sin C) + b³(sinCcos A – cos C sin A) + c³(sinAcosB – cos A sin B)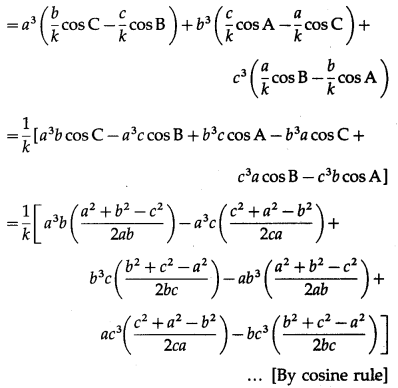

= 1/2k [a²(a² + b² – c²) – a²(a² + c² – b²) + b²(b² + c² – a²) – b²(a² + b² – c²) + c²(c² + a² – b²) – c²(b² + c² – a²)]
= 1/2k [a⁴ + a²b² – a²c² – a⁴ – a²c² + a²b² + b⁴ + b²c² – a²b² – a²b² – b⁴ + b²c² + c⁴ + a²c² – b²c² – b²c² – c⁴ + a²c²]
= 1/2k(0) = 0 = RHS.

Question 7.
In ∆ABC, if cot A, cot B, cot C are in A.P. then show that a², b², c² are also in A.P
Solution:
By the sine rule,

∴ sin A = ka, sin B = kb, sin C = kc …(1)
Now, cot A, cotB, cotC are in A.P.
∴ cotC – cotB = cotB – cot A
∴ cotA + cotC = 2cotB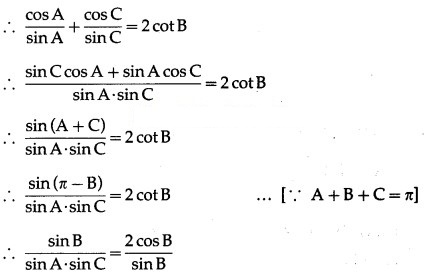

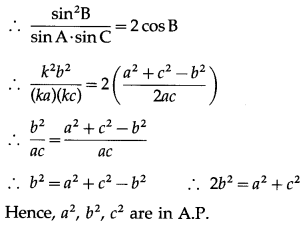
Question 8.
In ∆ABC, if a cos A = b cos B then prove that the triangle is right angled or an isosceles traingle.
Solution:
By the sine rule,

a = k sin A and b = k sin B
∴ a cos A = b cos B gives
k sin A cos A = k sin B cos B
∴ 2 sin A cos A = 2 sin B cos B
∴ sin 2A = sin 2B ∴ sin 2A – sin 2B = 0
∴ 2 cos (A + B)∙sin (A -B) = 0
∴ 2cos (π – C)∙sin(A – B) = 0 … [∵ A + B + C = π]
∴ -2 cos C∙sin (A – B) = 0
∴ cos C = 0 OR sin(A -B) = 0
∴ C = 90° OR A – B = 0
∴ C = 90° OR A = B
∴ the triangle is either rightangled or an isosceles triangle.

Question 9.
With usual notations prove that 2(bc cos A + ac cos B + ab cos C) = a² + b² + c².
Solution:
LHS = 2 (bc cos A + ac cos B + ab cos C)
= 2bc cos A + 2ac cos B + 2ab cos C
 = b² + c² – a² + c² + a² – b² + a² + b² – c² = a² + b² + c² = RHS.

Question 10.
In △ABC, if a = 18, b = 24, c = 30 then find the values of
(i) cos A
Solution:
Given : a = 18, b = 24 and c = 30
∴ 2s = a + b + c = 18 + 24 + 30 = 72 ∴ s = 36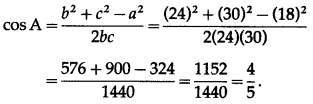

Solution:

Solution: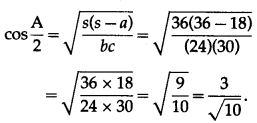

Solution: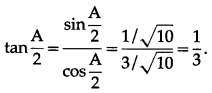

(v) A(△ABC)
Solution:

(iv) sin A.
Solution: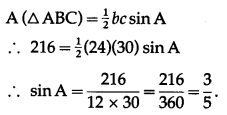

Question 11.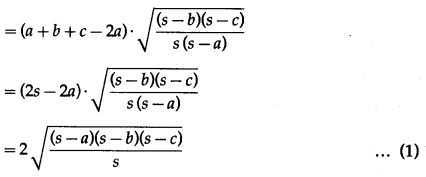

Question 12.