Question 1.
Fill in the blanks using correct alternatives.
i. Seg AB is parallel to Y-axis and co-ordinates of point A are (1, 3), then co-ordinates of point B can be _______.
(A) (3,1)
(B) (5,3)
(C) (3,0)
(D) (1,-3)
Answer: (D)
Since, seg AB || Y-axis.
∴ x co-ordinate of all points on seg AB
will be the same,
x co-ordinate of A (1, 3) = 1
x co-ordinate of B (1, – 3) = 1
∴ Option (D) is correct.
ii. Out of the following, point lies to the right of the origin on X-axis.
(A) (-2,0)
(B) (0,2)
(C) (2,3)
(D) (2,0)
Answer: (D)
iii. Distance of point (-3, 4) from the origin is _________.
(A) 7
(B) 1
(C) 5
(D) -5
Answer: (C)
Distance of (-3, 4) from origin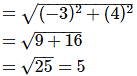
iv. A line makes an angle of 30° with the positive direction of X-axis. So the slope of the line is ________.
Answer: (C)
Question 2.
Determine whether the given points are collinear.
i. A (0, 2), B (1, -0.5), C (2, -3)
ii. P(1,2), Q(2,85),R(3,65)
iii L (1, 2), M (5, 3), N (8, 6)
Solution: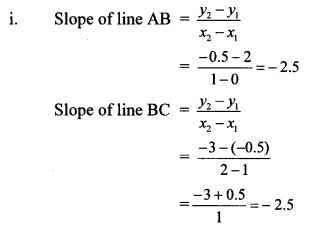
∴ slope of line AB = slope of line BC
∴ line AB || line BC
Also, point B is common to both the lines.
∴ Both lines are the same.
∴ Points A, B and C are collinear.
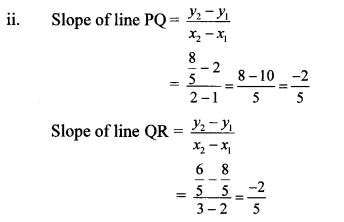
∴ slope of line PQ = slope of line QR
∴ line PQ || line QR
Also, point Q is common to both the lines.
∴ Both lines are the same.
∴ Points P, Q and R are collinear.
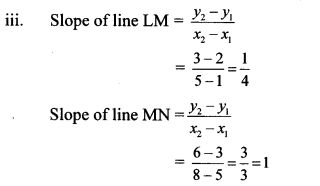
∴ slope of line LM ≠ slope of line MN
∴ Points L, M and N are not collinear.
[Note: Students can solve the above problems by using distance formula.]
Question 3.
Find the co-ordinates of the midpoint of the line segment joining P (0,6) and Q (12,20).
Solution:
P(x1,y1) = P (0, 6), Q(x2, y2) = Q (12, 20)
Here, x1 = 0, y1 = 6, x2 = 12, y2 = 20
∴ Co-ordinates of the midpoint of seg PQ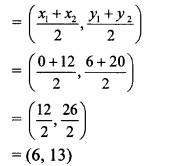
∴ The co-ordinates of the midpoint of seg PQ are (6,13).
Question 4.
Find the ratio in which the line segment joining the points A (3, 8) and B (-9, 3) is divided by the Y-axis.
Solution:
Let C be a point on Y-axis which divides seg AB in the ratio m : n.
Point C lies on the Y-axis
∴ its x co-ordinate is 0.
Let C = (0, y)
Here A (x1,y1) = A(3, 8)
B (x2, y2) = B (-9, 3)
∴ By section formula,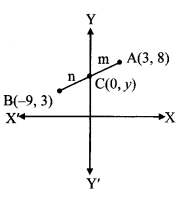
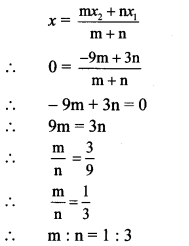
∴ Y-axis divides the seg AB in the ratio 1 : 3.
Question 5.
Find the point on X-axis which is equidistant from P (2, -5) and Q (-2,9).
Solution:
Let point R be on the X-axis which is equidistant from points P and Q.
Point R lies on X-axis.
∴ its y co-ordinate is 0.
Let R = (x, 0)
R is equidistant from points P and Q.
∴ PR = QR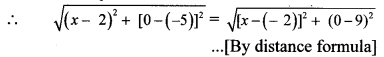
∴ (x – 2)2 + [0 – (-5)]2 = [x – (- 2)]2 + (0 – 9)2 …[Squaring both sides]
∴ (x – 2)2 + (5)2 = (x + 2)2 + (-9)2
∴ 4 – 4x + x2 + 25 = 4 + 4x + x2 + 81
∴ – 8x = 56
∴ x = -7
∴ The point on X-axis which is equidistant from points P and Q is (-7,0).
Question 6.
Find the distances between the following points.
i. A (a, 0), B (0, a)
ii. P (-6, -3), Q (-1, 9)
iii. R (-3a, a), S (a, -2a)
Solution:
i. Let A (x1, y1) and B (x2, y2) be the given points.
∴ x1 = a, y1 = 0, x2 = 0, y2 = a
By distance formula,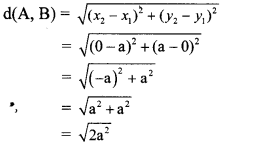
∴ d(A, B) = a2–√ units
ii. Let P (x1, y1) and Q (x2, y2) be the given points.
∴ x1 = -6, y1 = -3, x2 = -1, y2 = 9
By distance formula,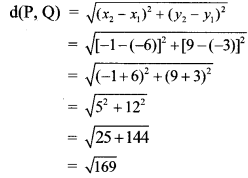
∴ d(P, Q) = 13 units
iii. Let R (x1, y1) and S (x2, y2) be the given points.
∴ x1 = -3a, y1 = a, x2 = a, y2 = -2a
By distance formula,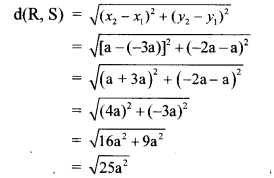
∴ d(R, S) = 5a units
Question 7.
Find the co-ordinates of the circumcentre of a triangle whose vertices are (-3,1), (0, -2) and (1,3).
Solution:
Let A (-3, 1), B (0, -2) and C (1, 3) be the vertices of the triangle.
Suppose O (h, k) is the circumcentre of ∆ABC.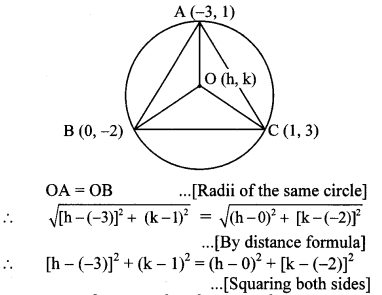
∴ (h + 3)2 + (k – 1)2 = h2 + (k + 2)2
∴ h2 + 6h + 9 + k2 – 2k + 1 = h2 + k2 + 4k + 4
∴ 6h – 2k + 10 = 4k + 4
∴ 6h – 2k – 4k = 4 – 10
∴ 6h – 6k = – 6
∴ h – k = -1 ,..(i)[Dividing both sides by 6]
OB = OC …[Radii of the same circle]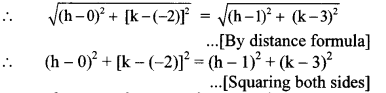
∴ h2 + (k + 2)2 = (h – 1)2 + (k – 3)2
∴ h2 + k2 + 4k + 4 = h2 – 2h + 1 + k2 – 6k + 9
∴ 4k + 4 = -2h + 1 – 6k + 9
∴ 2h+ 10k = 6
∴ h + 5k = 3 …(ii)
Subtracting equation (ii) from (i), we get
∴ The co-ordinates of the circumcentre of the triangle are ()
Question 8.
In the following examples, can the segment joining the given points form a triangle? If triangle is formed, state the type of the triangle considering sides of the triangle.
i. L (6, 4), M (-5, -3), N (-6, 8)
ii. P (-2, -6), Q (-4, -2), R (-5, 0)
iii. A(2–√,2–√),B(-2–√,-2–√),C(6–√,6–√)
Solution:
i. By distance formula,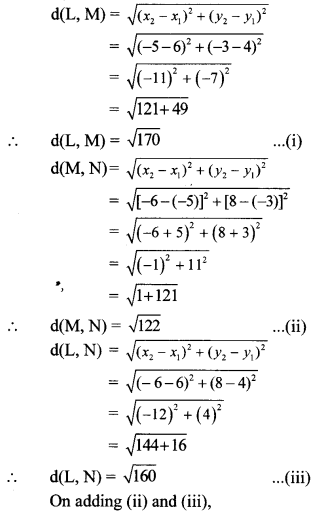
∴ d(M, N) + d (L, N) > d (L, M)
∴ Points L, M, N are non collinear points.
We can construct a triangle through 3 non collinear points.
∴ The segment joining the given points form a triangle.
Since MN ≠ LN ≠ LM
∴ ∆LMN is a scalene triangle.
∴ The segments joining the points L, M and N will form a scalene triangle.
ii. By distance formula,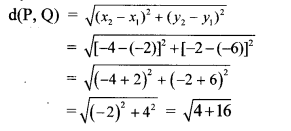
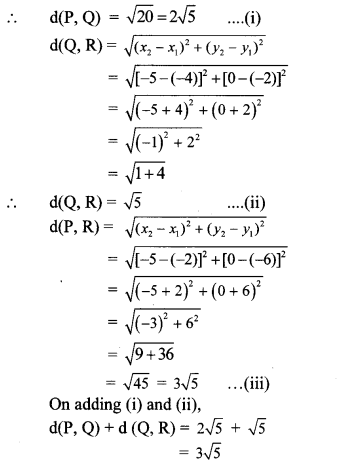
∴ d(P, Q) + d(Q, R) = d (P, R) …[From (iii)]
∴ Points P, Q, R are collinear points.
We cannot construct a triangle through 3 collinear points.
∴ The segments joining the points P, Q and R will not form a triangle.
iii. By distance formula,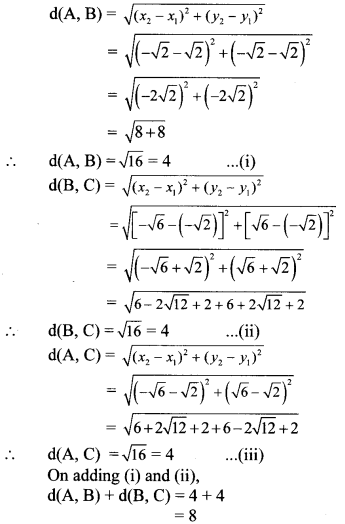
∴ d(A, B) + d(B, C) + d(A, C) … [From (iii)]
∴ Points A, B, C are non collinear points.
We can construct a triangle through 3 non collinear points.
∴ The segment joining the given points form a triangle.
Since, AB = BC = AC
∴ ∆ABC is an equilateral triangle.
∴ The segments joining the points A, B and C will form an equilateral triangle.
Question 9.
Find k, if the line passing through points P (-12, -3) and Q (4, k) has slope .
Solution:
P(x1,y1) = P(-12,-3),
Q(X2,T2) = Q(4, k)
Here, x1 = -12, x2 = 4, y1 = -3, y2 = k

Question 10.
Show that the line joining the points A (4,8) and B (5, 5) is parallel to the line joining the points C (2, 4) and D (1 ,7).
Proof:
∴ Slope of line AB = Slope of line CD
Parallel lines have equal slope.
∴ line AB || line CD
Question 11.
Show that points P (1, -2), Q (5, 2), R (3, -1), S (-1, -5) are the vertices of a parallelogram.
Proof:
By distance formula,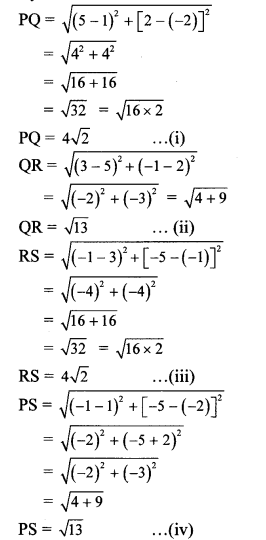
In ꠸PQRS,
PQ = RS … [From (i) and (iii)]
QR = PS … [From (ii) and (iv)]
∴ ꠸ PQRS is a parallelogram.
[A quadrilateral is a parallelogram, if both the pairs of its opposite sides are congruent]
∴ Points P, Q, R and S are the vertices of a parallelogram.
Question 12.
Show that the ꠸PQRS formed by P (2, 1), Q (-1, 3), R (-5, -3) and S (-2, -5) is a rectangle.
Proof:
By distance formula,
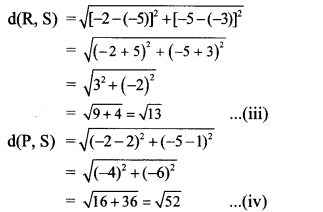
In ꠸PQRS,
PQ = RS …[From (i) and (iii)]
QR = PS …[From (ii) and (iv)]
꠸PQRS is a parallelogram.
[A quadrilateral is a parallelogram, if both the pairs of its opposite sides are congruent]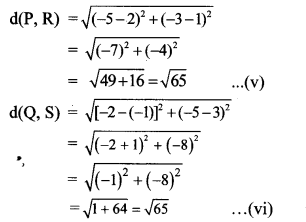
In parallelogram PQRS,
PR = QS … [From (v) and (vi)]
∴ ꠸PQRS is a rectangle.
[A parallelogram is a rectangle if its diagonals are equal]
Question 13.
Find the lengths of the medians of a triangle whose vertices are A (-1, 1), B (5, -3) and C (3,5).
Solution: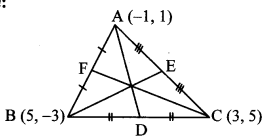
Suppose AD, BE and CF are the medians.
∴ Points D, E and F are the midpoints of sides BC, AC and AB respectively.
∴ By midpoint formula,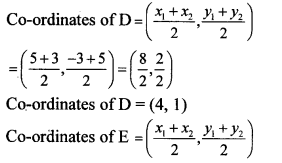
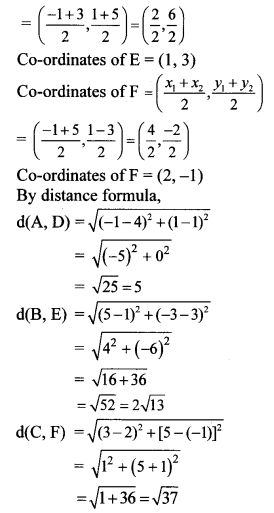
![]()
Question 14.
Find the co-ordinates of centroid of the triangle if points D (-7, 6), E (8, 5) and F (2, -2) are the mid points of the sides of that triangle.
Solution: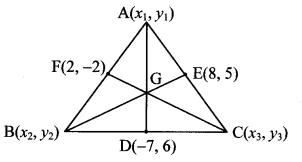
Suppose A (x1, y1), B (x2, y2) and C (x3, y3) are the vertices of the triangle.
D (-7, 6), E (8, 5) and F (2, -2) are the midpoints of sides BC, AC and AB respectively.
Let G be the centroid of ∆ABC.
D is the midpoint of seg BC.
By midpoint formula,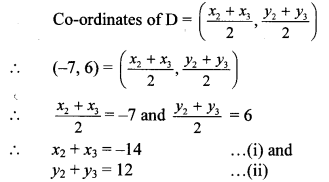
E is the midpoint of seg AC.
By midpoint formula,
Adding (i), (iii) and (v),
x2 + x3 + x1 + x3 + x1 + x2 = -14 + 16 + 4
∴ 2x1 + 2x2 + 2x3 = 6
∴ x1 + x2 + x3 = 3 …(vii)
Adding (ii), (iv) and (vi),
y2 + y3 + y1 + y3 + y1 +y2 = 12 + 10 – 4
∴ 2y1 + 2y2 + 2y3 = 18
∴ y1 + y2 + y3 = 9 …(viii)
G is the centroid of ∆ABC.
By centroid formula,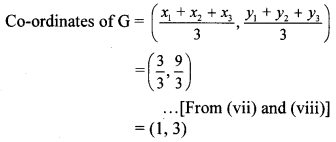
∴ The co-ordinates of the centroid of the triangle are (1,3).
Question 15.
Show that A (4, -1), B (6, 0), C (7, -2) and D (5, -3) are vertices of a square.
Proof:
By distance formula,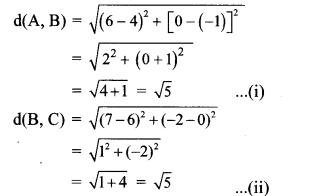
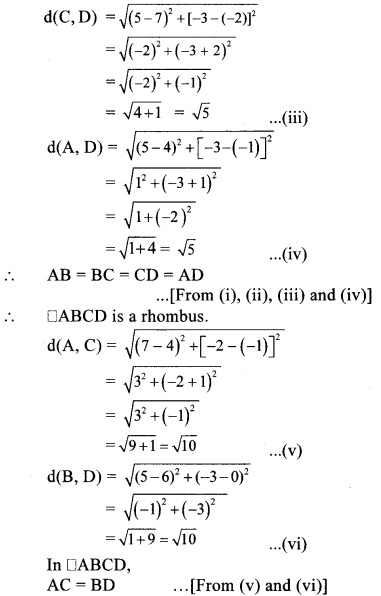
∴ □ABCD is a square.
[A rhombus is a square if its diagonals are equal]
Question 16.
Find the co-ordinates of circumcentre and radius of circumcircle of AABC if A (7, 1), B (3,5) and C (2,0) are given.
Solution:
Suppose, O (h, k) is the circumcentre of ∆ABC
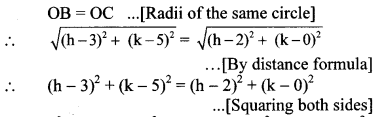
∴ h2 – 6h + 9 + k2 – 10k + 25 = h2 – 4h + 4 + k2
∴ 2h + 10k = 30
∴ h + 5k = 15 … (ii)[Dividing both sides by 2]
Multiplying equation (i) by 5, we get
25h + 5k = 115 …(iii)
Subtracting equation (ii) from (iii), we get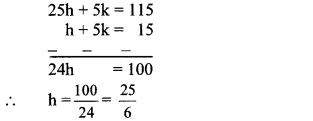
Substituting the value of h in equation (i), we get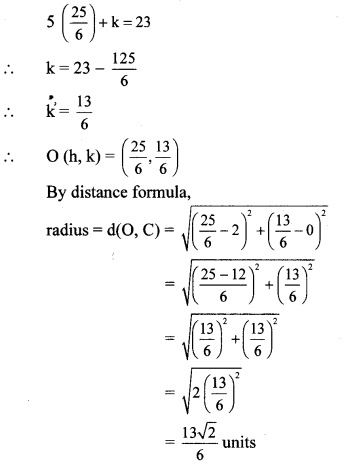

Question 17.
Given A (4, -3), B (8, 5). Find the co-ordinates of the point that divides segment AB in the ratio 3:1.
Solution:
Suppose point C divides seg AB in the ratio 3:1.
Here; A(x1, y1) = A (4, -3)
B (x2, y2) = B (8, 5)
By section formula,
∴ The co-ordinates of point dividing seg AB in ratio 3 : 1 are (7, 3).
Question 18.
Find the type of the quadrilateral if points A (-4, -2), B (-3, -7), C (3, -2) and D (2, 3) are joined serially.
Solution:
Slope of AB = slope of CD
∴ line AB || line CD
slope of BC = slope of AD
∴ line BC || line AD
Both the pairs of opposite sides of ∆ABCD are parallel.
∴ ꠸ ABCD is a parallelogram.
∴ The quadrilateral formed by joining the points A, B, C and D is a parallelogram.
Question 19.
The line segment AB is divided into five congruent parts at P, Q, R and S such that A-P-Q-R-S-B. If point Q (12, 14) and S (4, 18) are given, find the co-ordinates of A, P, R, B.
Solution:![]()
Points P, Q, R and S divide seg AB in five congruent parts.
Let A (x1, y1), B (x2, y2), P (x3, y3) and
R (x4, y4) be the given points.
Point R is the midpoint of seg QS.
By midpoint formula,
∴ co-ordinates of R are (8, 16).
Point Q is the midpoint of seg PR.
By midpoint formula,
∴ 28 = y3 + 16
∴ y3 = 12
∴ P(x3,y3) = (16, 12)
∴ co-ordinates of P are (16, 12).
Point P is the midpoint of seg AQ.
By midpoint formula,
∴ co-ordinates of A are (20, 10).
Point S is the midpoint of seg RB.
By midpoint formula,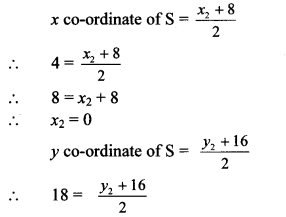
∴ 36 = y2 + 16
∴ y2 = 20
∴ B(x2, y2) = (0, 20)
∴ co-ordinates of B are (0, 20).
∴ The co-ordinates of points A, P, R and B are (20, 10), (16, 12), (8, 16) and (0, 20) respectively.
Question 20.
Find the co-ordinates of the centre of the circle passing through the points P (6, -6), Q (3, -7) and R (3,3).
Solution:
Suppose O (h, k) is the centre of the circle passing through the points P, Q and R.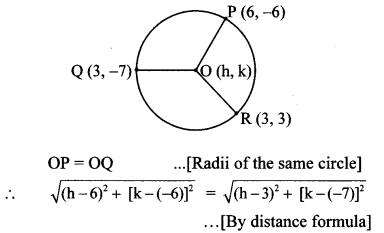
∴ (h – 6)2 + (k + 6)2 = (h – 3)2 + (k + 7)2
∴ h2 – 12h + 36 + k2 + 12k + 36
= h2 – 6h + 9 + k2 + 14k + 49
∴ 6h + 2k = 14
∴ 3h + k = 7 …(i)[Dividing both sides by 2]
OP = OR …[Radii of the same circle]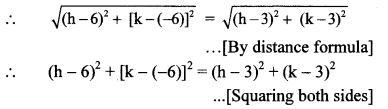
∴ (h – 6)2 + (k + 6)2 = (h – 3)2 + (k – 3)2
∴ h2 – 12h + 36 + k2 + 12k + 36
= h2 – 6h + 9 + k2 – 6k + 9
∴ 6h – 18k = 54
∴ 3h – 9k = 27 …(ii)[Dividing both sides by 2]
Subtracting equation (ii) from (i), we get
Substituting the value of k in equation (i), we get
3h – 2 = 7
∴ 3h = 9
∴ h = 93 = 3
∴ The co-ordinates of the centre of the circle are (3, -2).
Question 21.
Find the possible pairs of co-ordinates of the fourth vertex D of the parallelogram, if three of its vertices are A (5, 6), B (1, -2) and C (3, -2).
Solution: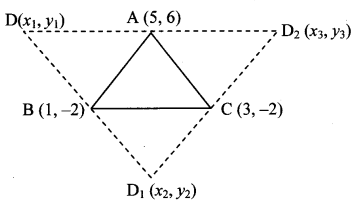
Let the points A (5, 6), B (1, -2) and C (3, -2) be the three vertices of a parallelogram.
The fourth vertex can be point D or point Di or point D2 as shown in the figure.
Let D(x1,y1), D, (x2, y2) and D2 (x3,y3).
Consider the parallelogram ACBD.
The diagonals of a parallelogram bisect each other.
∴ midpoint of DC = midpoint of AB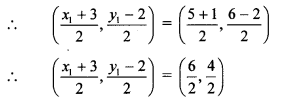
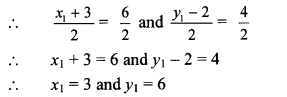
Co-ordinates of point D(x1, y1) are (3, 6).
Consider the parallelogram ABD1C.
The diagonals of a parallelogram bisect each other.
∴ midpoint of AD1 = midpoint of BC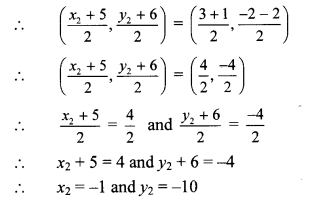
∴ Co-ordinates of D1(x2,y2) are (-1,-10).
Consider the parallelogram ABCD2.
The diagonals of a parallelogram bisect each other.
∴ midpoint of BD2 = midpoint of AC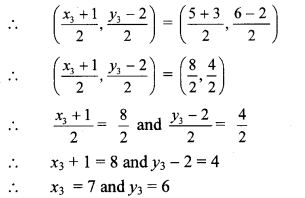
∴ co-ordinates of point D2 (x3, y3) are (7, 6).
∴ The possible pairs of co-ordinates of the fourth vertex D of the parallelogram are (3, 6), (-1,-10) and (7,6).
Question 22.
Find the slope of the diagonals of a quadrilateral with vertices A (1, 7), B (6,3), C (0, -3) and D (-3,3).
Solution:
Suppose ABCD is the given quadrilateral.
∴ The slopes of the diagonals of the quadrilateral are 10 and 0.
