Chapter 5 Quadrilaterals Practice Set 5

Question 1.
Choose the correct alternative answer and fill in the blanks.

i. If all pairs of adjacent sides of a quadrilateral are congruent, then it is called ____.
(A) rectangle
(B) parallelogram
(C) trapezium
(D) rhombus
Answer:
(D) rhombus

ii. If the diagonal of a square is 22√2 cm, then the perimeter of square is ____.
(A) 24 cm
(B) 24√2 cm
(C) 48 cm
(D) 48√2 cm
Answer:
In ∆ABC,
AC² = AB² + BC²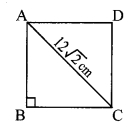

∴ (12² √2 )² = AB² + AB²

∴ AB = 12 cm
∴ Perimeter of □ABCD = 4 x 12 = 48 cm
(C) 48 cm

iii. If opposite angles of a rhombus are (2x)° and (3x – 40)°, then the value of x is ____.
(A) 100°
(B) 80°
(C) 160°
(D) 40°
Answer:
2x = 3x – 40 … [Pythagoras theorem]
∴ x = 40°
(D) 40°

Question 2.
Adjacent sides of a rectangle are 7 cm and 24 cm. Find the length of its diagonal.
Solution: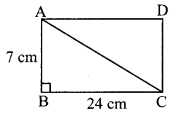

Let □ABCD be the rectangle.
AB = 7 cm, BC = 24 cm
In ∆ABC, ∠B = 90° [Angle of a rectangle]
AC² = AB² + BC² [Pythagoras theorem]
= 7² + 24²
= 49 + 576
= 625
AC = √625 [Taking square root of both sides]
= 25 cm
∴ The length of the diagonal of the rectangle is 25 cm.

Question 3.
If diagonal of a square is 13 cm, then find its side.
Solution: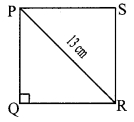

Let □PQRS be the square of side x cm.
∴ PQ = QR = x cm …..(i) [Sides of a square]
∴ In ∆PQR, ∠Q = 90° [Angle of a square]
∴ PR² = PQ² + QR² [Pythagoras theorem]
∴ 13 = x + x [From (i)]
∴ 169 = 2x²

The length of the side of the square is 6.5√2 cm.

Question 4.
Ratio of two adjacent sides of a parallelogram is 3 : 4, and its perimeter is 112 cm. Find the length of its each side.
Solution:

Let □STUV be the parallelogram.
Ratio of two adjacent sides of a parallelogram is 3 : 4.
Let the common multiple be x.
ST = 3x cm and TU = 4x cm
∴ ST = UV = 3x cm
TU = SV = 4x cm …..(i) [Opposite sides of a parallelogram]
Perimeter of □STUV = 112 [Given]
∴ ST + TU + UV + SV = 112
∴ 3x + 4x + 3x + 4x = 112 [From (i)]
∴ 14x = 112

∴ x = 8
∴ ST = UV = 3x = 3 x 8 = 24 cm
∴ TU = SV = 4x = 4 x 8 = 32 cm [From (i)]
∴ The lengths of the sides of the parallelogram are 24 cm, 32 cm, 24 cm and 32 cm.

Question 5.
Diagonals PR and QS of a rhombus PQRS are 20 cm and 48 cm respectively. Find the length of side PQ.
Solution: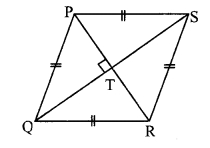

□PQRS is a rhombus. [Given]
PR = 20 cm and QS = 48 cm [Given]

ii. In ∆PQT, ∠PTQ = 90° [Diagonals of a rhombus are perpendicular to each other]
∴ PQ² = PT² + QT² [Pythagoras- theorem]
= 10² + 24²
= 100 + 576
∴ PQ² = 676

= 26 cm
∴ The length of side PQ is 26 cm.

Question 6.
Diagonals of a rectangle PQRS are intersecting in point M. If ∠QMR = 50°, then find the measure of ∠MPS.
Solution: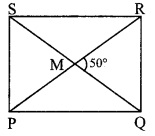

□PQRS is a rectangle.

Also, PR = QS …..(iii) [Diagonals of a rectangle are congruent]
∴ PM = MS ….(iv) [From (i), (ii) and (iii)]
In ∆PMS,
PM = MS [From (iv)]
∴ ∠MSP = ∠MPS = x° …..(v) [Isosceles triangle theorem]
∠PMS = ∠QMR = 50° ……(vi) [Vertically opposite angles]
In ∆MPS,
∠PMS + ∠MPS + ∠MSP = 180° [Sum of the measures of the angles of a triangle is 180°]
∴ 50° +x + x = 180° [From (v) and (vi)]
∴ 50° + 2x= 180
∴ 2x= 180-50
∴ 2x= 130

∴ ∠MPS = 65° [From (v)]

Question 7.
In the adjoining figure, if seg AB || seg PQ , seg AB ≅ seg PQ, seg AC || seg PR, seg AC ≅ seg PR, then prove that seg BC || seg QR and seg BC ≅ seg QR.

Solution:
Given: seg AB || seg PQ , seg AB ≅ seg PQ,
seg AC || seg PR, seg AC ≅ seg PR
To prove: seg BC || seg QR, seg BC ≅ seg QR
Proof:
Consider □ABQP,
seg AB || seg PQ [Given]
seg AB ≅ seg PQ [Given]
∴ □ABQP is a parallelogram. [A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and congruent]
∴ segAP || segBQ …..(i)
∴ seg AP ≅ seg BQ …..(ii) [Opposite sides of a parallelogram]
Consider □ACRP,
seg AC || seg PR [Given]
seg AC ≅ seg PR [Given]
∴ □ACRP is a parallelogram. [A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and congruent]
∴ seg AP || seg CR …(iii)
∴ seg AP ≅ seg CR …….(iv) [Opposite sides of a parallelogram]
Consider □BCRQ,
seg BQ || seg CR
seg BQ ≅ seg CR
∴ □BCRQ is a parallelogram. [A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and congruent]
∴ seg BC || seg QR
∴ seg BC ≅ seg QR [Opposite sides of a parallelogram]

Question 8.
In the adjoining figure, □ABCD is a trapezium. AB || DC. Points P and Q are midpoints of seg AD and seg BC respectively. Then prove that PQ || AB and PQ = 12 ( AB + DC).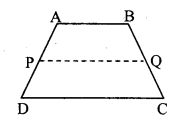

Given : □ ABCD is a trapezium.
To prove:
Construction: Join points A and Q. Extend seg AQ and let it meet produced DC at R.
Proof:

seg AB || seg DC [Given]
and seg BC is their transversal.
∴ ∠ABC ≅ ∠RCB [Alternate angles]
∴ ∠ABQ ≅ ∠RCQ ….(i) [B-Q-C]
In ∆ABQ and ∆RCQ,
∠ABQ ≅∠RCQ [From (i)]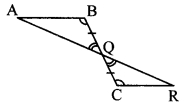

seg BQ ≅ seg CQ [Q is the midpoint of seg BC]
∠BQA ≅ ∠CQR [Vertically opposite angles]
∴ ∆ABQ ≅ ∆RCQ [ASA test]
seg AB ≅ seg CR …(ii) [c. s. c. t.]
seg AQ ≅ seg RQ [c. s. c. t.]
∴ Q is the midpoint of seg AR. ….(iii)

In ∆ADR,
Points P and Q are the midpoints of seg AD and seg AR respectively. [Given and from (iii)]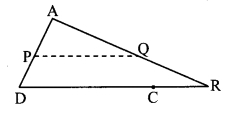

∴ seg PQ || seg DR [Midpoint theorem]
i.e. seg PQ || seg DC ……..(iv) [D-C-R]
But, seg AB || seg DC …….(v) [Given]
∴ seg PQ || seg AB [From (iv) and (v)]
In ∆ADR,

Question 9.
In the adjoining figure, □ABCD is a trapezium. AB || DC. Points M and N are midpoints of diagonals AC and DB respectively, then prove that MN || AB.

Solution:
Given: □ABCD is a trapezium. AB || DC.
Points M and N are midpoints of diagonals AC and DB respectively.
To prove: MN || AB
Construction: Join D and M. Extend seg DM to meet seg AB at point E such that A-E-B.
Proof:
seg AB || seg DC and seg AC is their transversal. [Given]
∴ ∠CAB ≅ ∠ACD [Alternate angles]
∴ ∠MAE ≅ ∠MCD ….(i) [C-M-A, A-E-B]
In ∆AME and ∆CMD,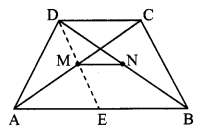

∠AME ≅ ∠CMD [Vertically opposite angles]
seg AM ≅ seg CM [M is the midpoint of seg AC]
∠MAE ≅∠MCD [From (i)]
∴ ∆AME ≅ ∆CMD [ASA test]
∴ seg ME ≅ seg MD [c.s.c.t]
∴ Point M is the midpoint of seg DE. …(ii)
In ∆DEB,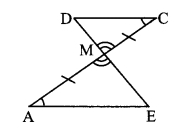

Points M and N are the midpoints of seg DE and seg DB respectively. [Given and from (ii)]
∴ seg MN || seg EB [Midpoint theorem]
∴ seg MN || seg AB [A-E-B]

Intext Questions and Activities

Question 1.
Draw five parallelograms by taking various measures of lengths and angles. (Textbook page no. 59)

Question 2.
Draw a parallelogram PQRS. Draw diagonals PR and QS. Denote the intersection of diagonals by letter O. Compare the two parts of each diagonal with a divider. What do you find? (Textbook page no. 60)

Answer:
seg OP = seg OR, and seg OQ = seg OS
Thus we can conclude that, point O divides the diagonals PR and QS in two equal parts.

Question 3.
To verify the different properties of quadrilaterals.

Material: A piece of plywood measuring about 15 cm x 10 cm, 15 thin screws, twine, scissor.
Note: On the plywood sheet, fix five screws in a horizontal row keeping a distance of 2 cm between any two adjacent screws. Similarly make two more rows of screws exactly below the first one. Take care that the vertical distance between any two adjacent screws is also 2 cm.
With the help of the screws, make different types of quadrilaterals of twine. Verify the properties of sides and angles of the quadrilaterals. (Textbook page no. 75)