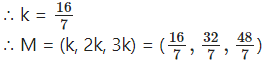Chapter 5 Vectors Ex 5.4

Question 1.

Solution:

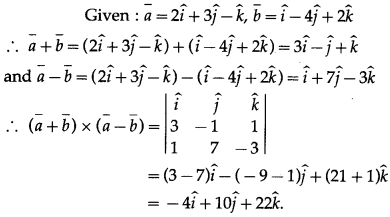
Question 2.

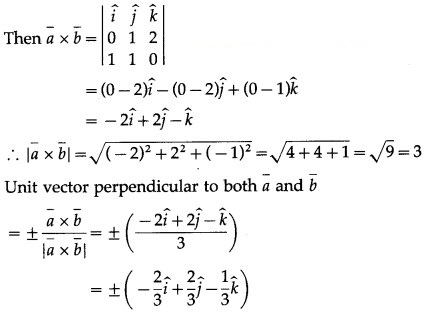
Question 3.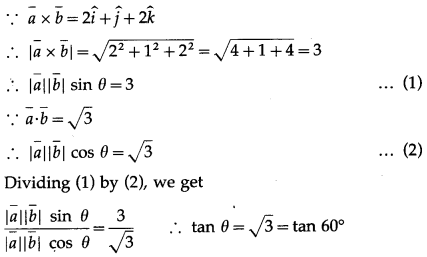


∴ θ = 60°.

Question 4.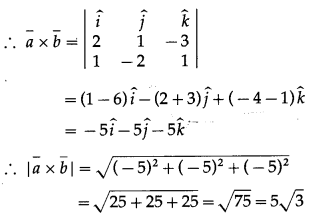


∴ unit vectors perpendicular to both the vectors a¯ and b¯.

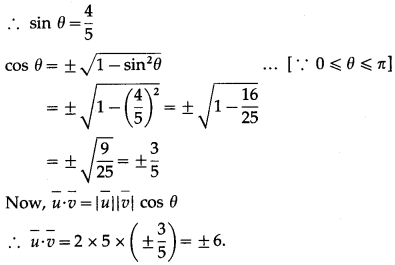
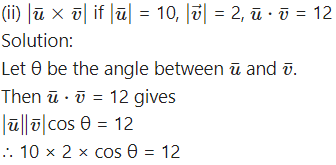
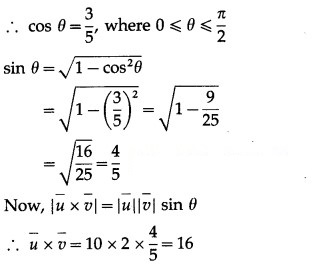
Question 6.

Solution:

Question 7.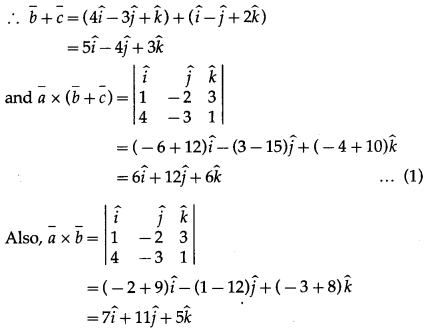

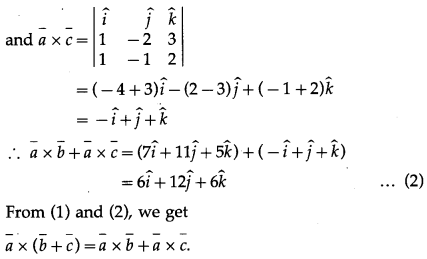
Question 8.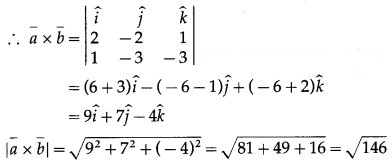

Question 9.

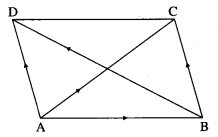
Question 10.
Find the area of parallelogram whose diagonals are determined by the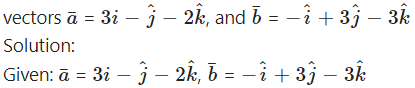 

Question 11.

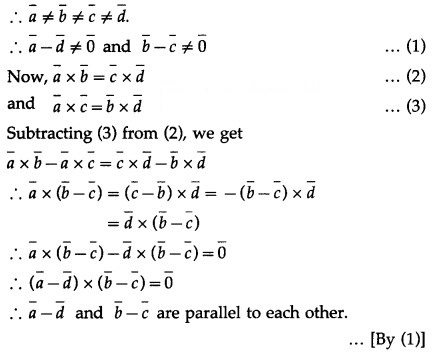
Question 12.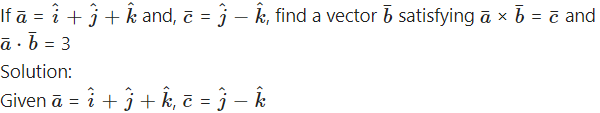


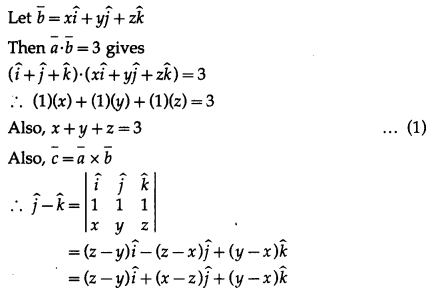
By equality of vectors,
z – y = 0 ….(2)
x – z = 1 ……(3)
y – x = -1 ……(4)
From (2), y = z.
From (3), x = 1 + z
Substituting these values of x and y in (1), we get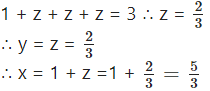

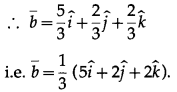
Question 13.

Solution: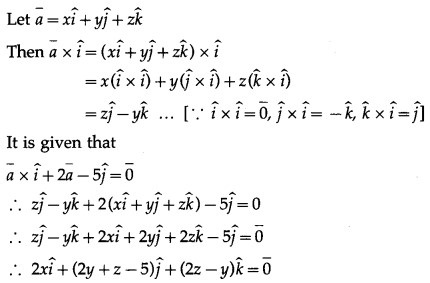

By equality of vectors
2x = 0 i.e. x = 0
2y + z – 5 = 0 … (1)
2z – y = 0 … (2)
From (2), y = 2z
Substituting y = 2z in (1), we get
4z + z = 5 ∴ z = 1
∴ y = 2z = 2(1) = 2
∴ x = 0, y = 2, z = 1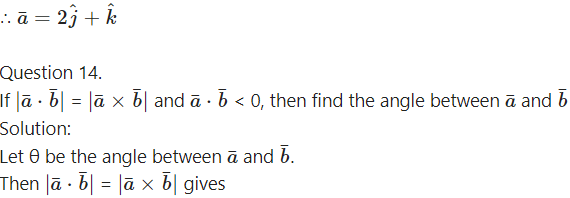

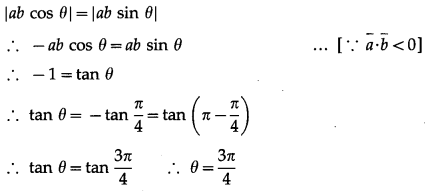
Question 15.
Prove by vector method that sin (α + β) = sinα∙cosβ+cosα∙sinβ.
Solution: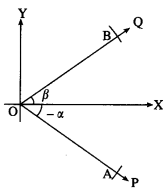

Let ∠XOP and ∠XOQ be in standard position and m∠XOP = -α, m∠XOQ = β.
Take a point A on ray OP and a point B on ray OQ such that
OA = OB = 1.
Since cos (-α) = cos α
and sin (-α) = -sin α,
A is (cos (-α), sin (-α)),
i.e. (cos α, – sin α)
B is (cos β, sin β)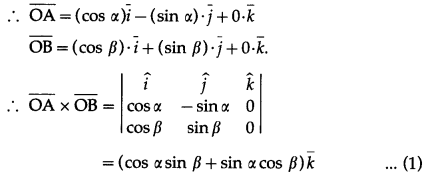

Question 16.
Find the direction ratios of a vector perpendicular to the two lines whose direction ratios are
(i) -2, 1, -1 and -3, -4, 1
Solution:
Let a, b, c be the direction ratios of the vector which is perpendicular to the two lines whose direction ratios are -2, 1, -1 and -3, -4, 1
∴ -2a + b – c = 0 and -3a – 4b + c = 0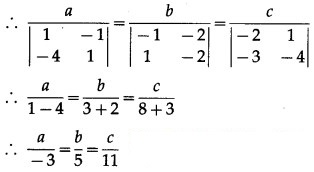



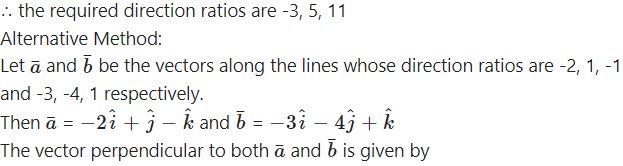
Hence, the required direction ratios are -3, 5, 11.

(ii) 1, 3, 2 and -1, 1, 2
Solution:

Question 17.
Solution:
Given, al + bm + cn = 0 …(1)
and fmn + gnl + hlm = 0 …..(2)

Substituting this value of n in equation (2), we get
(fm + gl)∙[latex]-\left(\frac{a l+b m}{c}\right)[/latex] + hlm = 0
∴ -(aflm + bfm² + agl² + bglm) + chlm = 0
∴ agl² + (af + bg – ch)lm + bfm² = 0 … (4)
Note that both l and m cannot be zero, because if l = m = 0, then from (3), we get
n = 0, which is not possible as l² + m² + n² = 1.
Let us take m # 0.
Dividing equation (4) by m², we get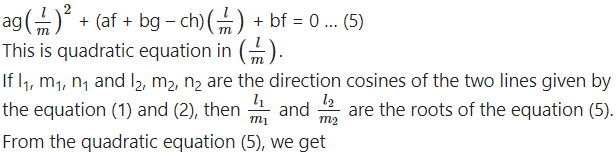

Question 18.
If A(1, 2, 3) and B(4, 5, 6) are two points, then find the foot of the perpendicular from the point B to the line joining the origin and point A.
Solution: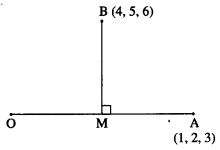

Let M be the foot of the perpendicular drawn from B to the line joining O and A.
Let M = (x, y, z)
OM has direction ratios x – 0, y – 0, z – 0 = x, y, z
OA has direction ratios 1 – 0, 2 – 0, 3 – 0 = 1, 2, 3
But O, M, A are collinear.

∴ x = k, y = 2k, z = 3k
∴ M = (k, 2k, 3k)
∵ BM has direction ratios
k – 4, 2k – 5, 3k – 6
BM is perpendicular to OA
∴ (l)(k – 4) + 2(2k – 5) + 3(3k – 6)
∴ = k – 4 + 4k – 10 + 9k – 18 = 0
∴ 14k = 32