Chapter 6 Line and Plane Ex 6.1

Question 1.

Question 2.

Question 3.

Question 4.

Solution:

Question 5.

Question 6.
Find the Cartesian equations of the line passing through A(-1, 2, 1) and having direction ratios 2, 3, 1.
Solution:
The cartesian equations of the line passing through (x₁, y₁, z₁) and having direction ratios a, b, c are

∴ the cartesian equations of the line passing through the point (-1, 2, 1) and having direction ratios 2, 3, 1 are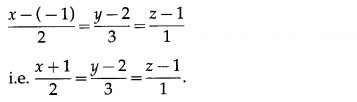

Question 7.
Find the Cartesian equations of the line passing through A(2, 2, 1) and B(1, 3, 0).
Solution:
The cartesian equations of the line passing through the points (x₁, y₁, z₁) and (x₂, y₂, z₂) are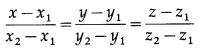

Here, (x₁, y₁, z₁) = (2, 2, 1) and (x₂, y₂, z₂) = (1, 3, 0)
∴ the required cartesian equations are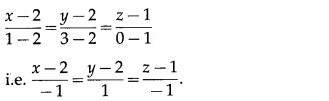

Question 8.
A(-2, 3, 4), B(1, 1, 2) and C(4, -1, 0) are three points. Find the Cartesian equations of the line AB and show that points A, B, C are collinear.
Solution:
We find the cartesian equations of the line AB. The cartesian equations of the line passing through the points (x₁, y₁, z₁) and (x₂, y₂, z₂) are

Here, (x₁, y₁, z₁) = (-2, 3, 4) and (x₂, y₂, z₂) = (4, -1, 0)
∴ the required cartesian equations of the line AB are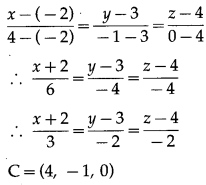


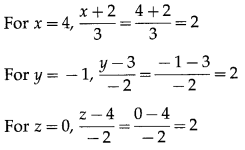
∴ coordinates of C satisfy the equations of the line AB.
∴ C lies on the line passing through A and B.
Hence, A, B, C are collinear.

Question 9.

Solution:
The equations of the lines are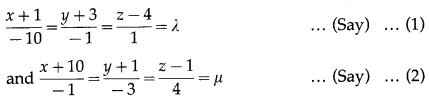

From (1), x = -1 -10λ, y = -3 – 2, z = 4 + λ
∴ the coordinates of any point on the line (1) are
(-1 – 10λ, – 3 – λ, 4 + λ)
From (2), x = -10 – u, y = -1 – 3u, z = 1 + 4u
∴ the coordinates of any point on the line (2) are
(-10 – u, -1 – 3u, 1 + 4u)
Lines (1) and (2) intersect, if
(- 1 – 10λ, – 3 – λ, 4 + 2) = (- 10 – u, -1 – 3u, 1 + 4u)
∴ the equations -1 – 10λ = -10 – u, -3 – 2= – 1 – 3u
and 4 + λ = 1 + 4u are simultaneously true.
Solving the first two equations, we get, λ = 1 and u = 1. These values of λ and u satisfy the third equation also.
∴ the lines intersect.
Putting λ = 1 in (-1 – 10λ, -3 – 2, 4 + 2) or u = 1 in (-10 – u, -1 – 3u, 1 + 4u), we get
the point of intersection (-11, -4, 5).

Question 10.

Solution: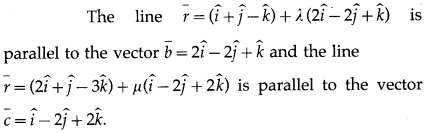

The vector perpendicular to the vectors b¯ and c¯ is given by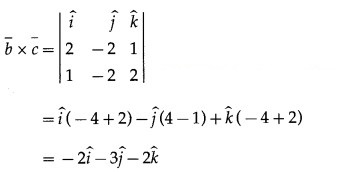


∴ the equation of the required line is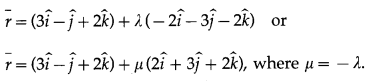

Question 11.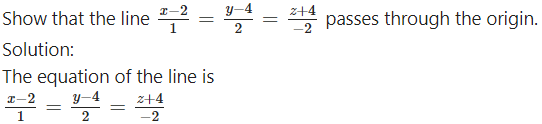


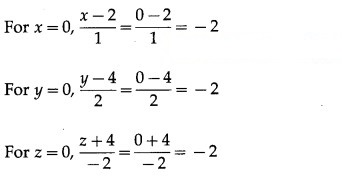
∴ coordinates of the origin O satisfy the equation of the line.
Hence, the line passes through the origin.