Chapter 6 Statistics Set 6.2

Question 1.
The following table shows classification of number of workers and the number of hours they work in a software company. Find the median of the number of hours they work.

Solution:

Cumulative frequency which is just greater than (or equal) to 500 is 650.
∴ The median class is 10 – 12.
Now, L = 10, f = 500, cf = 150, h = 2

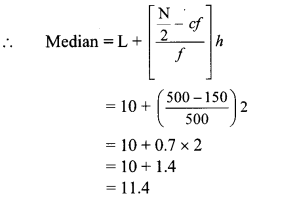
∴ The median of the number of hours the workers work is 11.4 hours.

Question 2.
The frequency distribution table shows the number of mango trees in a grove and their yield of mangoes. Find the median of data.

Solution: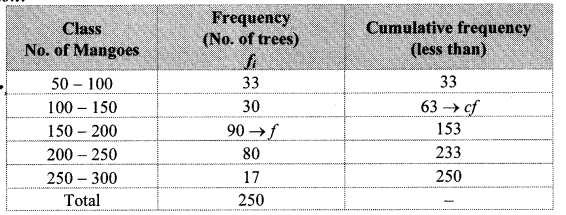

Here, total frequency = ∑f_i = N = 250

Cumulative frequency which is just greater than (or equal) to 125 is 153.
∴ The median class is 150 – 200.
Now, L = 150, f = 90, cf = 63, h = 50

∴ The median of the given data is 184 mangoes (approx).

Question 3.
The following table shows the classification of number of vehicles and their speeds on Mumbai-Pune express way. Find the median of the data.

Solution: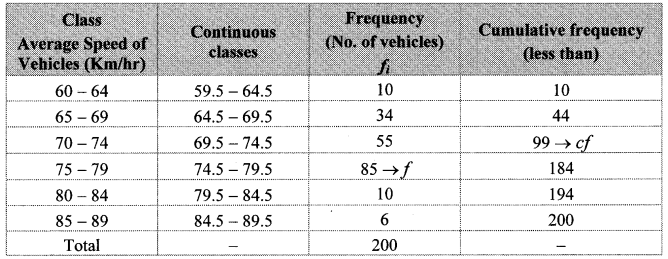

Here, total frequency = ∑f_i = N = 200

Cumulative frequency which is just greater than (or equal) to 100 is 184.
∴ The median class is 74.5 – 79.5.
Now, L = 74.5, f = 85, cf = 99, h = 5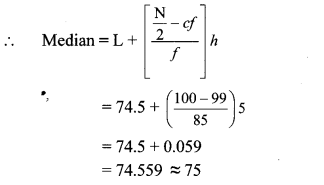

∴ The median of the given data is 75 km/hr (approx.).

Question 4.
The production of electric bulbs in different factories is shown in the following table. Find the median of the productions.

Solution: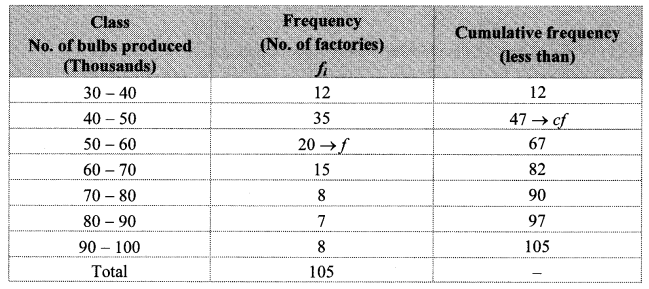

Cumulative frequency which is just greater than (or equal) to 52.5 is 67.
∴ The median class is 50 – 60.
Now, L = 50, f = 20, cf = 47, h = 10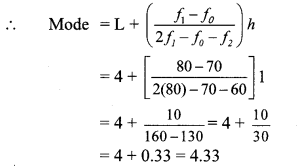

∴ The median of the productions is 52750 bulbs (approx.).

Question 1.

Solution:

The sequence of the terms of scores is 1,2, 3, …….., m, m + 1, m + 2, …, 2m + 1
Thus, we have to prove that m + 1 is the middle term if the number of scores is 2m + 1
i.e. to prove
number of terms from 1 to m = number of terms from m + 2 to 2m + 1 …(i)
Consider the L.H.S. of equation (i)
The sequence is an A.P. with a = 1,d = 1, t_n1 = m
t_n1 = a + (n₁ – 1) d
∴ m = 1 + (n₁ – 1)1
∴ m = 1 + n₁ – 1
∴ m = n₁
Consider the R.H.S. of equation (ii)
The sequence is an A.P. with a = m + 2, d = 1, t_n2 = 2m + 1
t_n2 = a + (n₂ – 1)d
∴ 2m + 1 = m + 2 + (n₂ – 1)1
∴ 2m + 1 = m + n₂ + 1
∴ m = n₂
∴ number of terms from 1 to m = number of terms from m + 2 to 2m + 1 = m = 
∴ m + 1 is the middle term if the number of scores is 2m + 1.

Solution:

The sequence of the terms of scores is 1, 2, 3 … m – 1, m, m + 1, m + 2,…., 2m
Thus, we have to prove that m and m + 1 are the middlemost terms if the number of scores is 2m.
i.e. to prove
number of terms from 1 to m – 1 = number of terms from m + 2 to 2m …(i)
Consider the L.H.S. of equation (i)
The sequence is an A.P. with a = 1, d = 1, t_n1 = m – 1
t_n1 = a + (n₁ – 1)d
∴ m – 1 = 1 + (n₁ – 1)1
∴m – 1 = 1 + n₁ – 1
∴ n₁ = m – 1
Consider the R.H.S. of equation (i)
The sequence is an A.P. with a = m + 2, d = 1, t_n2= 2m
t_n2= a + (n₂ – 1) d
∴ 2m = m + 2 + (n₂ – 1)1
∴ 2m = m + 2 + n₂ – 1
∴ n₂ = m – 1
∴ number of terms from 1 to m – 1 = number of terms from m + 2 to 2m = m – 1 = 
∴ m and m + 1 are the middlemost terms if the number of scores is 2m.