Question 1.
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
Solution:
Let AB represent the height of the church and point C represent the position of the person.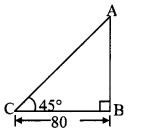
BC = 80 m
Angle of elevation = ∠ACB = 45°
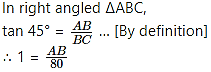
∴ AB = 80m
∴ The height of the church is 80 m.
Question 2.
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse. (√3 = 1.73)
Solution:
Let AB represent the height of lighthouse and point C represent the position of the ship.
AB = 90 m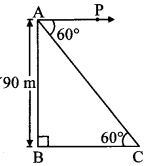
Angle of depression = ∠PAC = 60°
Now, ray AP || seg BC
∴ ∠ACB = ∠PAC … [Alternate angles]
∴ ∠ACB = 60°
In right angled ∆ABC,![]()
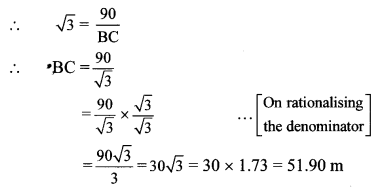
∴ The ship is 51.90 m away from the lighthouse.
Question 3.
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building?
Solution:
Let AB and CD represent the heights of the two buildings, and BD represent the width of the road.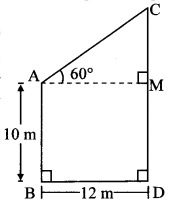
Draw seg AM ⊥ seg CD.
Angle of elevation = ∠CAM = 60°
AB = 10 m
BD= 12 m
In ꠸ABDM,
∠B = ∠D = 90°
∠M = 90° … [seg AM ⊥ seg CD]
∴ ∠A = 90° … [Remaining angle of ꠸ABDM]
∴ ꠸ABDM is a rectangle …. [Each angle is 90°]
∴ AM = BD = 12 m opposite sides
DM = AB = 10 m of a rectangle
Question 4.
Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops is 22 metre. Find the angle made by the wire with the horizontal.
Solution:
Let AB and CD represent the heights of two poles, and AC represent the length of the wire.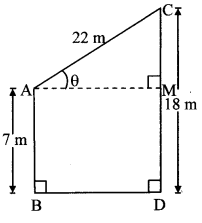
Draw seg AM ⊥ seg CD.
Angle of elevation = ∠CAM = θ
AB = 7 m
CD = 18 m
AC = 22 m
In ꠸ABDM,
∠B = ∠D = 90°
∠M = 90° …[seg AM ⊥ seg CD]
∴ ∠A = 90° … [Remaining angle of ꠸ABDM]
∴ □ABDM is a rectangle. … [Each angle is 90°]
∴ DM = AB = 7 m … [Opposite sides of a rectangle]
Now, CD = CM + DM … [C – M – D]
∴ 18 = CM + 7
∴ CM = 18 – 7 = 11 m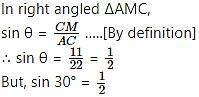
∴ θ = 30°
∴ The angle made by the wire with the horizontal is 30°.
Question 5.
A storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of 60° with the horizontal. Find the height of the tree.
Solution:
Let AB represent the height of the tree.
Suppose the tree broke at point C and its top touches the ground at D.
AC is the broken part of the tree which takes position CD such that ∠CDB = 60°
∴ AC = CD …(i)
BD = 20 m
In right angled ∆CBD,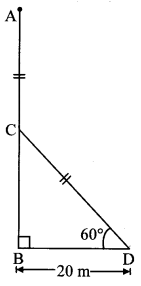
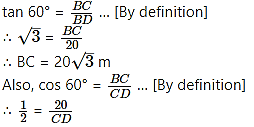
∴ CD = 20 × 2 = 40 m
∴ AC = 40 m …[From(i)]
Now, AB = AC + BC ….[A – C – B]
= 40 + 20√3
= 40 + 20 × 1.73
= 40 + 34.6
= 74.6
∴ The height of the tree is 74.6 m.
Question 6.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string. (√3 = 1.73)
Solution:
Let AB represent the height at which kite is flying and point C represent the point where the string is tied at the ground.
∠ACB is the angle made by the string with the ground.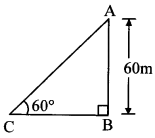
∠ACB = 60°
AB = 60 m
In right angled ∆ABC,
sin 60° = ABAC … [By definition]
∴ AC = 40 √3 = 40 × 1.73 = 69.20 m
∴ The length of the string is 69.20 m.
