Maharashtra State Board Class 7th Maths Chapter 1 Geometrical Constructions Set 1.2 Solution

Question 1.
Draw triangles with the measures given below:
i. In ∆ABC, l(AB) = 5.5 cm, l(BC) = 4.2 cm, l(AC) = 3.5 cm.
ii. In ∆STU, l(ST) = 7 cm, l(TU) = 4 cm, l(SU) = 5 cm.
iii. In ∆PQR, l(PQ) = 6 cm, l(QR) = 3.8 cm, l(PR) = 4.5 cm.
Solution:
i. In ∆ABC, l(AB) = 5.5 cm, l(BC) = 4.2 cm, l(AC) = 3.5 cm.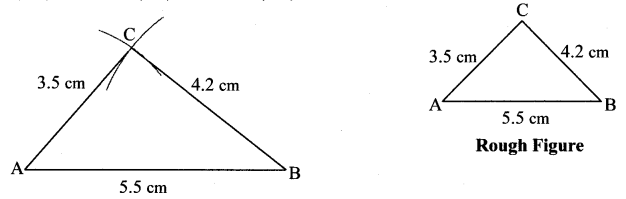

ii. In ∆STU, l(ST) = 7 cm, l(TU) = 4 cm, l(SU) = 5 cm.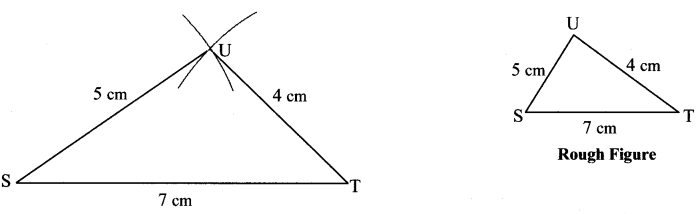

iii. In ∆PQR, l(PQ) = 6 cm, l(QR) = 3.8 cm, l(PR) = 4.5 cm.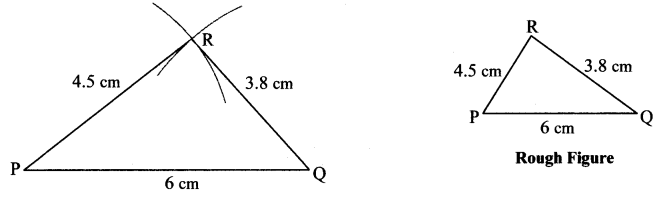

Question 2.
Draw an isosceles triangle with base 5 cm and the other sides 3.5 cm each.
Solution: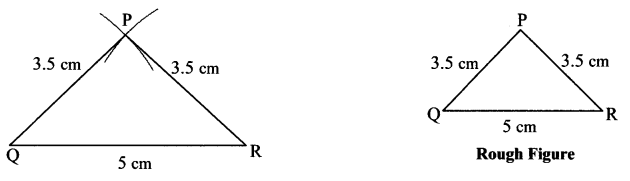

Question 3.
Draw an equilateral triangle with side 6.5 cm.
Solution: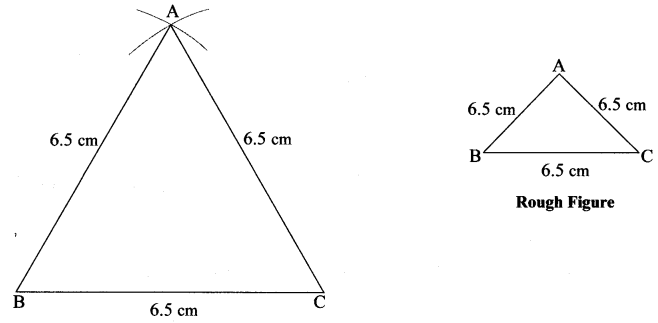

Question 4.
Choose the lengths of the sides yourself and draw one equilateral, one isosceles and one scalene triangle.
Solution:
i. Equilateral triangle LMN, l(LM) = l(MN) = l(LN) = 4 cm.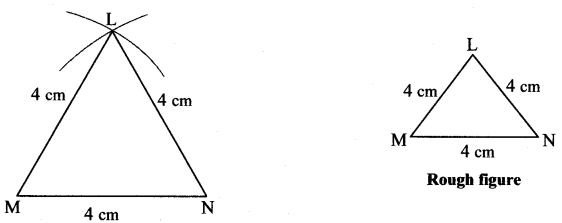

ii. Isosceles triangle STU, l(ST) = l(TU) = 4cm, l(SU) = 6 cm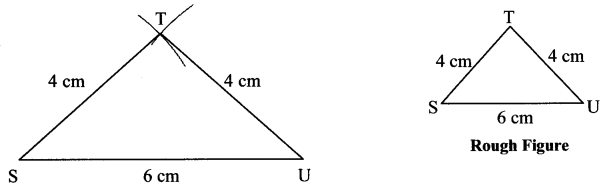

iii. Scalene triangle XYZ, l(XY) = 4.5 cm, l(XY) = 6.5 cm, l(XZ) = 5.5 cm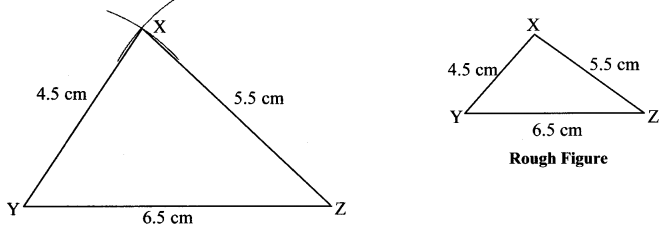

Intext Questions and Activities

Question 1.
Draw ∆ABC such that l(AB) = 4 cm, and l(BC) = 3 cm. (Textbook pg. no. 3)

1. Can this triangle be drawn?
2. A number of triangles can be drawn to fulfill these conditions. Try it out.
3. Which further condition must be placed if we are to draw a unique triangle using the above information?

Solution:

1. ∆ABC triangle cannot be drawn as length of third side is not given.
2. For ∆ABC to draw l(AC) > l(AB) + l(BC)
   i.e., l(AC) > 4 + 3
   i.e., l(AC) > 7 cm
   ∴ number of triangles can be drawn if l(AC) > 7 cm
3. l(AC) > l(AB) + l(BC) is the required condition to draw a unique triangle.