Maharashtra Board Class 11 Maths Part 1 Chapter 2 Trigonometry – I Ex 2.1 Solution

Question 1.
Find the trigonometric functions of 0°, 30°, 45°, 60°, 150°, 180°, 210°, 300°, 330°, – 30°, – 45°, – 60°, – 90°, – 120°, – 225°, – 240°, – 270°, – 315°
Solution:
Angle of measure 0°: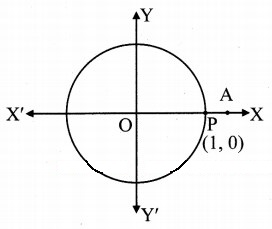

Let m∠XOA = 0° = 0^c
Its terminal arm (ray OA) intersects the standard
unit circle in P(1, 0).
Hence,x = 1 and y = 0
sin 0° = y = 0,
cos 0° = x = 1,

Angle of measure 30°:
Let m∠XOA = 30°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y)
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP= 1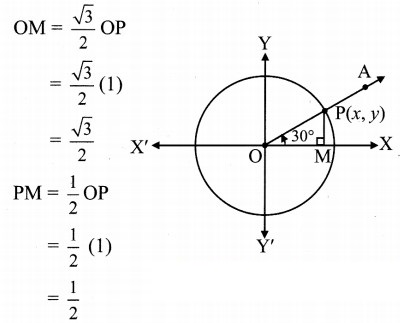

Since point P lies in 1st quadrant, x > 0, y > 0

Angle of measure 45°:
Let m∠XOA = 45°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 45° – 45° – 90° triangle.
OP = 1,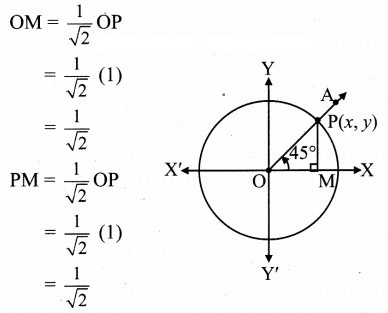

Since point P lies in the 1st quadrant, x > 0, y > 0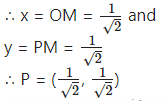

Angle of measure 60°:
Let m∠XOA = 60°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP= 1,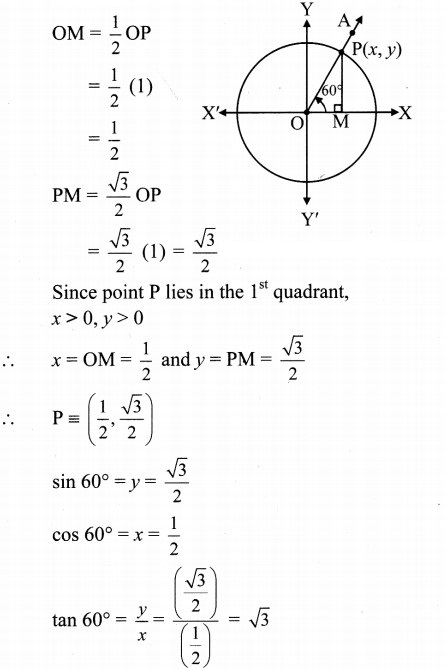

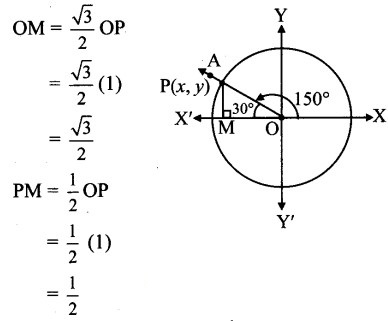
Angle of measure 150°:
Let m∠XOA = 150°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP= 1,

Since point P lies in the 2nd quadrant, x < 0, y > 0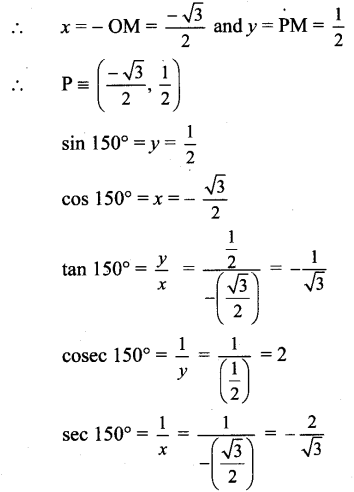

Angle of measure 180°:
Let m∠XOA = 180°
Its terminal arm (ray OA) intersects the standard unit circle at P(-1, 0).
∴ x = – 1 and y = 0
sin 180° =y = 0
cos 180° = x = -1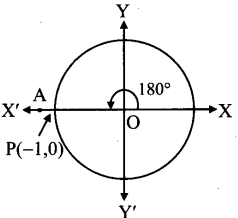

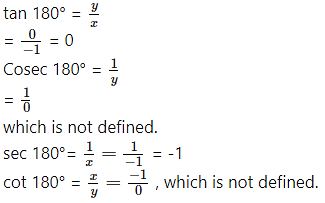
Angle of measure 210°:
Let m∠XOA = 210°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP= 1,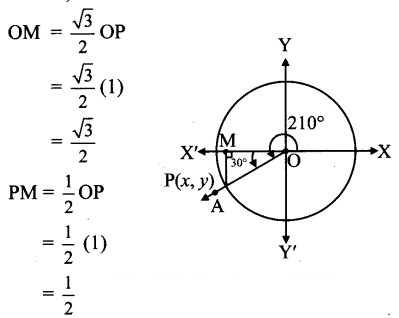

Since point P lies in the 3rd quadrant, x < 0,y < 0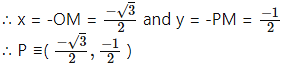


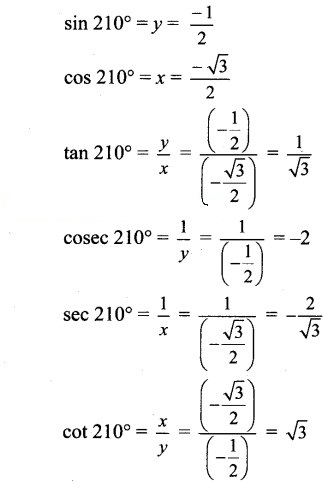
Angle of measure 300°:
Let m∠XOA = 300°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP = 1,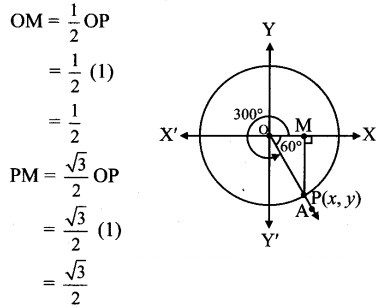

Since point P lies in the 1st quadrant, x > 0,y > 0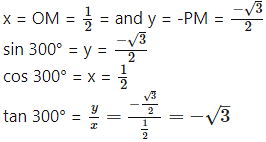

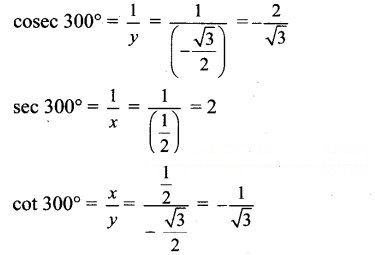
Angle of measure 330°:
Let m∠XOA = 330°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP= 1,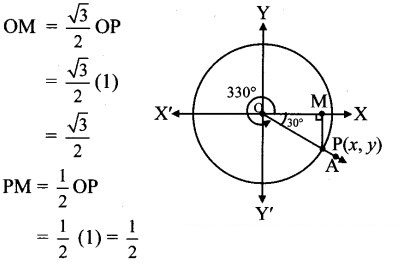

Since point P lies in the 4th quadrant, x > 0, y < 0

Angle of measure 30°
Let m∠XOA = -30°
Its terminal arm (ray OA) intersects the standard unit circle at P(x,y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60 — 90° triangle.
op = 1,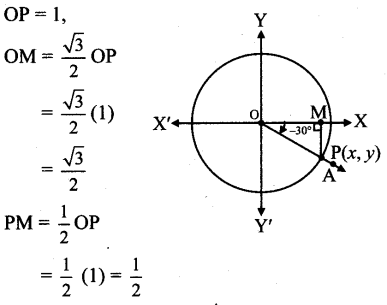

Since point P lies in the 4th quadrant x > 0, y < 0

Angle of measure 45°:
Let m∠XOA = 45°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 45° – 45° – 90° triangle.
OP = 1,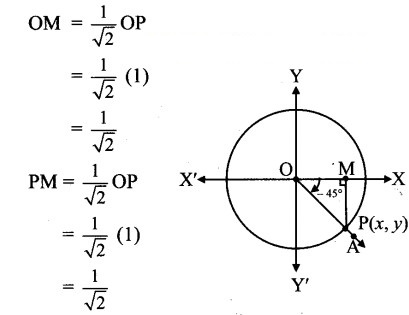

Since point P lies in the 4th quadrant x > 0, y < 0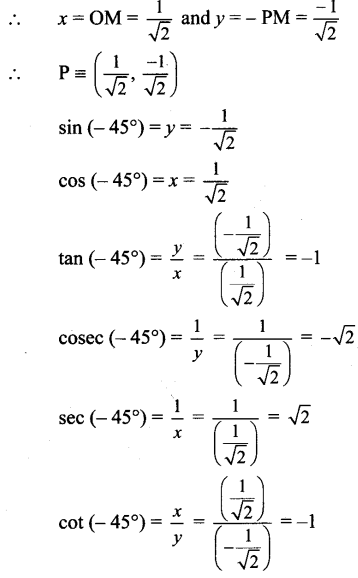

[Note : Answer given in the textbook of sin (45°) = – 1/2. However, as per our 

Angle of measure (-60°):
Let m∠XOA = -60°
Its terminal arm (ray OA) intersects the standard
unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
ΔOMP is a 30° – 60° – 90° triangle.
OP = 1,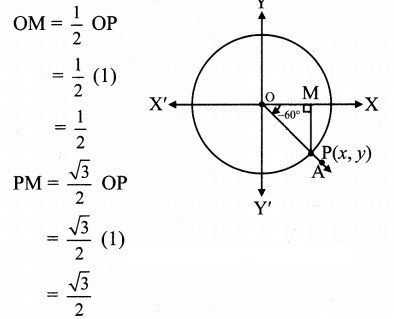

Since point P lies in the 4’ quadrant,
x > 0, y < 0

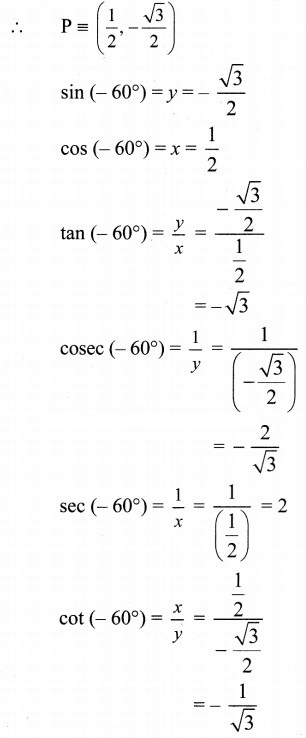
Angle of measure (-90°):
Let m∠XOA = -90°
It terminal arm (ray OA) intersects the standard unit circle at P(0, -1)
∴ x = 0 and y = -1
sin (-90°) = y = -1
cos (-90°) = s = 0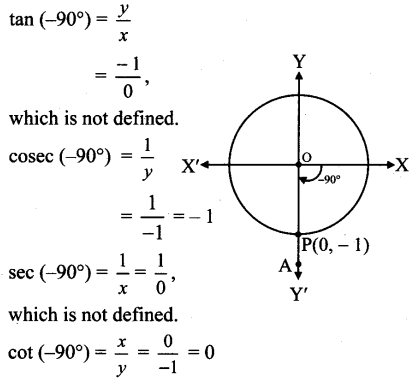

Angle of measure (-120°):
Let m∠XOA = – 120°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30° – 60° – 90° triangle.
OP = 1,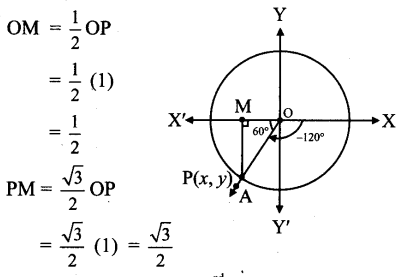

Since point P lies in the 3rd quadrant, x < 0, y < 0

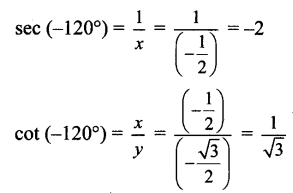
Angle of measure (- 225°):
Let m∠XOA = – 225°
Its terminal arm (ray OA) intersects the standard unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
ΔOMP is a 45° – 45° – 90° triangle.
OP = 1,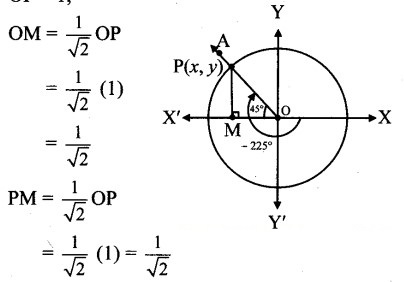

Since point P lies in the 2nd quadrant, x < 0, y > 0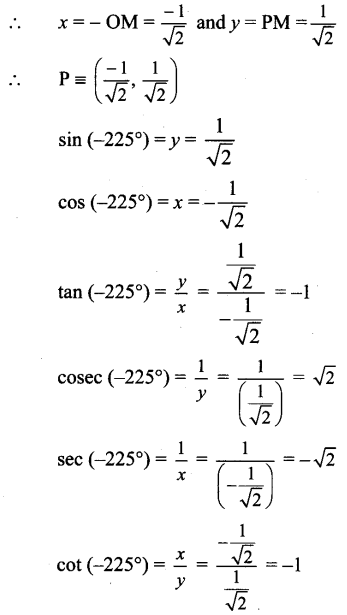

Angle of measure 2400):
Let m∠XOA = 240°
Its terminal arm (ray OA) intersects the standard
unit circle at P(x, y).
Draw seg PM perpendicular to the X-axis.
∴ ΔOMP is a 30°  – 60° –  900 triangle.

Since point P lies in the 2nd quadrant, x<0, y>0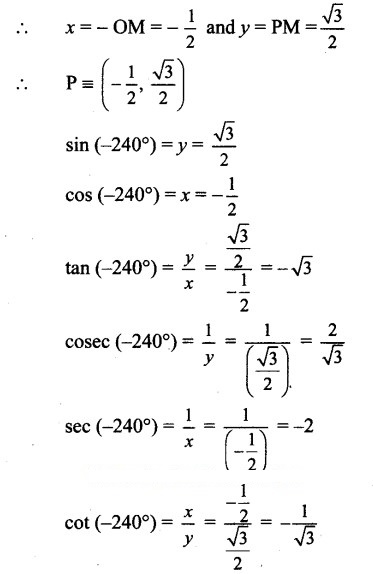

Angle of measure (- 270°):
Let m∠XOA = – 270°
Its terminal arm (ray OA)
intersects the standard unit,
circle at P(0, 1).
∴ x = 0 and y = 1
sin (- 270°) = y = 1
cos (- 270°) = x = 0

which is not defined.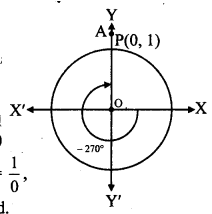

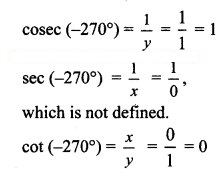
Angle of measure ( 315°):
Let m∠XOA 315°
Its terminal arm (ray OA) intersects the standard unit circle at P(x,y).
Draw seg PM perpendicular to the X-axis.
ΔOMP is a 45° – 45° – 90° triangle.
OP = 1,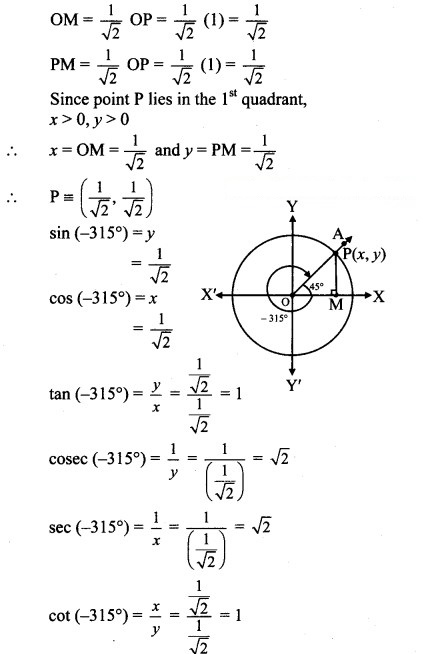

Question 2.
State the signs of:
i. tan 380°
ii. cot 230°
iii 468°
Solution:
1. 380° = 360° + 20°
∴ 380° and 20° are co-terminal angles.
Since 0° < 20° <90°0,
20° lies in the l quadrant.
∴ 380° lies in the 1st quadrant,
∴ tan 380° is positive.

ii. Since, 180° <230° <270°
∴ 230° lies in the 3rd quadrant.
∴ cot 230° is positive.

iii. 468° = 360°+108°
∴ 468° and 108° are co-terminal angles.
Since 90° < 108° < 180°,
108° lies in the 2nd quadrant.
∴ 468° lies in the 2nd quadrant.
∴ sec 468° is negative.

Question 3.
State the signs of cos 4^c and cos 4°. Which of these two functions is greater?
Solution:
Since 0° < 4° < 90°, 4° lies in the first quadrant. ∴ cos4° >0 …(i)
Since 1^c = 57° nearly,
180° < 4^c < 270°
∴ 4^c lies in the third quadrant.
∴ cos 4^c < 0 ………(ii)
From (i) and (ii),
cos 4° is greater.

Question 4.
State the quadrant in which 6 lies if
i. sin θ < 0 and tan θ > 0
ii. cos θ < 0 and tan θ > 0
Solution:
i. sin θ < 0 sin θ is negative in 3rd and 4th quadrants, tan 0 > 0
tan θ is positive in 1st and 3rd quadrants.
∴ θ lies in the 3rd quadrant.

ii. cos θ < 0 cos θ is negative in 2nd and 3rd quadrants, tan 0 > 0
tan θ is positive in 1st and 3rd quadrants.
∴ θ lies in the 3rd quadrant.

Question 5.
Evaluate each of the following:
i. sin 30° + cos 45° + tan 180°
ii. cosec 45° + cot 45° + tan 0°
iii. sin 30° x cos 45° x lies tan 360°
Solution:
i. We know that,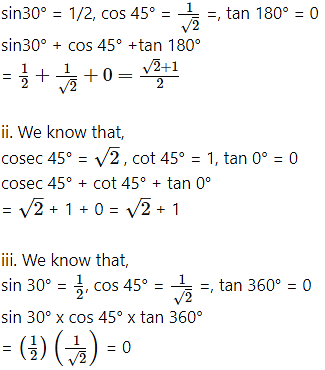

Question 6.
Find all trigonometric functions of angle in standard position whose terminal arm passes through point (3, – 4).
Solution:
Let θ be the measure of the angle in standard position whose terminal arm passes through P(3, -4).
∴ x = 3 and y = -4
r = OP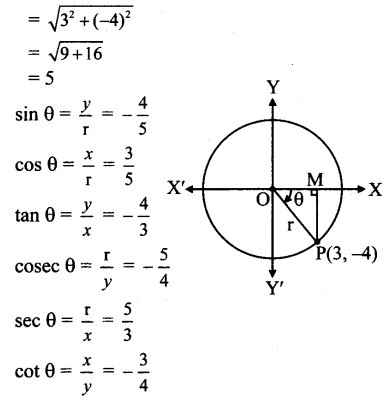

Question 7.

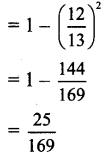
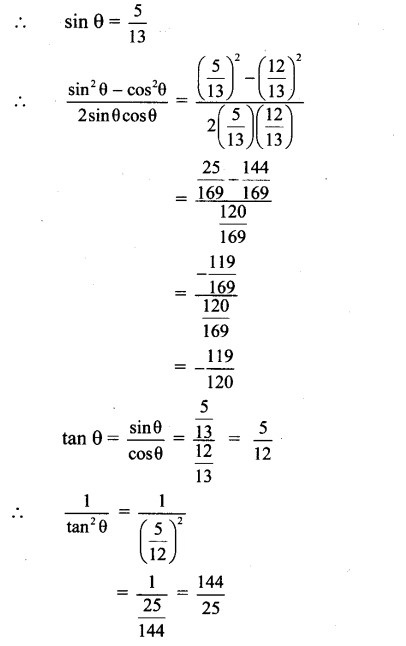
Question 8.
Using tables evaluate the following: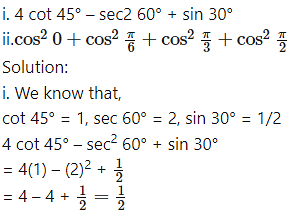

ii. We know that,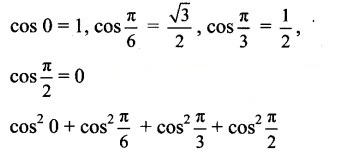

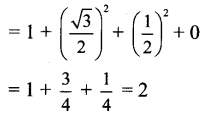
Question 9.


Since A lies in the 2nd quadrant,
tan A < 0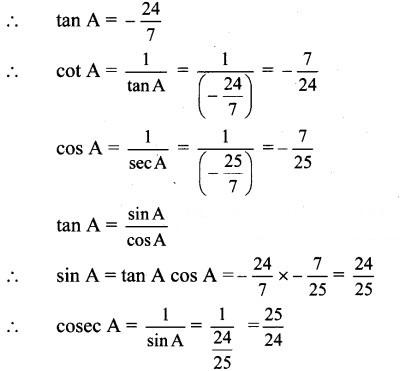

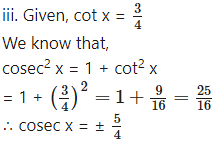
Since x lies in the 3rd quadrant, cosec x < 0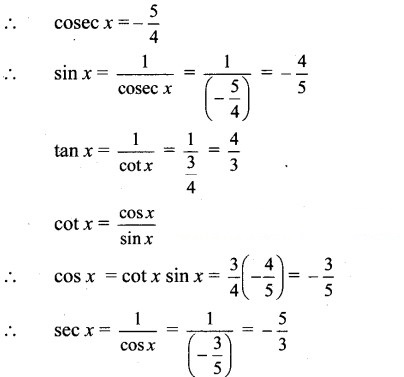

Since x lies in the 4th quadrant,
sec x > 0