Question 1.
Find the slope, x-intercept, y-intercept of each of the following lines, i. 2x + 3y-6 = 0 ii. 3x-y-9 = 0 iii. x + 2y = 0
Solution:
i. Given equation of the line is 2x + 3y – 6 = 0.
Comparing this equation with ax + by + c = 0,
we get
a = 2, b = 3, c = -6
ii. Given equation of the line is 3x – y – 9 = 0.
Comparing this equation with ax + by + c = 0,
we get
a = 3, b = – 1, c = – 9
iii. Given equation of the line is x + 2y = 0.
Comparing this equation with ax + by + c = 0,
we get
a = 1, b = 2, c = 0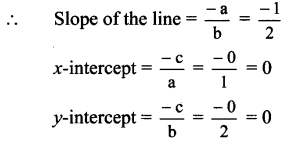
Question 2.
Write each of the following equations in ax + by + c = 0 form.
i. y = 2x – 4
ii. y = 4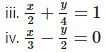
i. y = 2x – 4
∴ 2x – y – 4 = 0 is the equation in ax + by + c = 0 form.
ii. y = 4
∴ 0x + 1y – 4 = 0 is the equation in ax + by + c = 0 form.
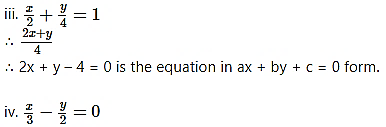
∴ 2x – 3y = 0
∴ 2x – 3y + 0 = 0 is the equation in ax + by + c = 0 form.
[Note: Answer given in the textbook is ‘2x – 3y – 6 = 0’. However, as per our calculation it is ‘2x-3y + 0 = 0’.]
Question 3.
Show that the lines x – 2y – 7 = 0 and 2x – 4y + 15 = 0 are parallel to each other.
Solution: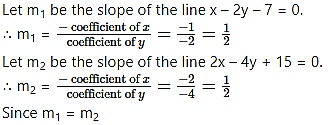
the given lines are parallel to each other.
Question 4.
Show that the lines x – 2y – 7 = 0 and 2x + y + 1 = 0 are perpendicular to each other. Find their point of intersection.
Solution: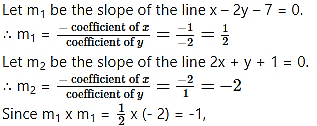
the given lines are perpendicular to each other. Consider,
x – 2y – 7 = 0 …(i)
2x + y + 1 =0 …(ii)
Multiplying equation (ii) by 2, we get
4x + 2y + 2 = 0 …(iii)
Adding equations (i) and (iii), we get
5x – 5 = 0
∴ x = 1
Substituting x = 1 in equation (ii), we get
2 + y + 1 = 0
∴ y = – 3
∴ The point of intersection of the given lines is (1,-3).
Question 5.
If the line 3x + 4y = p makes a triangle of area 24 square units with the co-ordinate axes, then find the value of p.
Solution:
Let the line 3x + 4y = p cuts the X and Y axes at points A and B respectively.
3x + 4y = p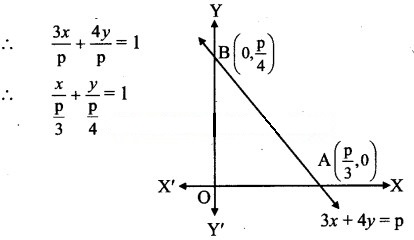

Question 6.
Find the co-ordinates of the foot of the perpendicular drawn from the point A(- 2,3) to the line 3x-y -1 = 0.
Solution:
Let M be the foot of perpendicular drawn from
point A(- 2,3) to the line
3x-y- 1 = 0 …(i)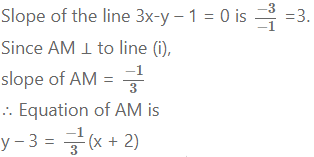
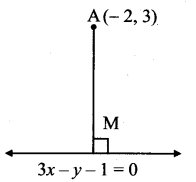
∴ 3(y – 3) = – 1(x + 2)
∴ 3y – 9 = -x – 2
∴ x + 3y – 7 = 0 …………(ii)
The foot of perpendicular i.e., point M, is the point of intersection of equations (i) and (ii).
By (i) x 3 + (ii), we get 10x -10 = 0
∴ x = 1
Substituting x = 1 in (ii), we get
1 + 3y – 7 = 0
∴ 3y = 6
∴ y = 2
∴ The co-ordinates of the foot of the perpendicular Mare (1,2).
Question 7.
Find the co-ordinates of the circumcentre of the triangle whose vertices are A(- 2, 3), B(6, -1), C(4,3),e
Solution:
Here, A(-2, 3), B(6, -1), C(4, 3) are the vertices of ∆ABC.
Let F be the circumcentre of AABC.
Let FD and FE be the perpendicular bisectors of the sides BC and AC respectively.
∴ D and E are the midpoints of side BC and AC respectively.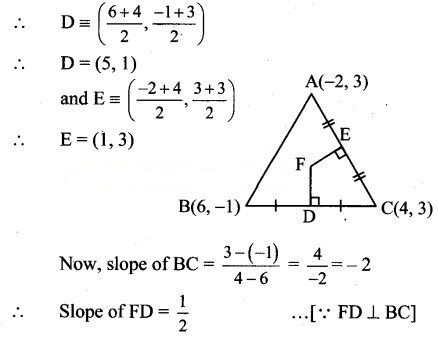
Since FD passes through (5, 1) and has slope 1/2 equation of FD is![]()
∴ 2 (y – 1) = x – 5
∴ 2y – 2 = x – 5
∴ x – 2y – 3 = 0 …(i)
Since both the points A and C have same y co-ordinates i.e. 3,
the given points lie on the line y = 3.
Since the equation FE passes through E(1, 3),
the equation of FE is x = 1. .. .(ii)
To find co-ordinates of circumcentre, we have to solve equations (i) and (ii).
Substituting the value of x in (i), we get
1 – 2y -3 = 0
∴ y = -1
∴ Co-ordinates of circumcentre F ≡ (1, – 1).
Question 8.
Find the co-ordinates of the orthocentre of the triangle whose vertices are A(3, – 2), B(7,6), C (-1,2).
Solution:
Let O be the orthocentre of ∆ABC.
Let AD and BE be the altitudes on the sides BC and AC respectively.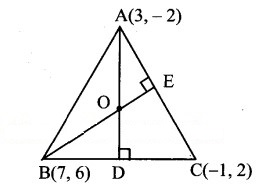
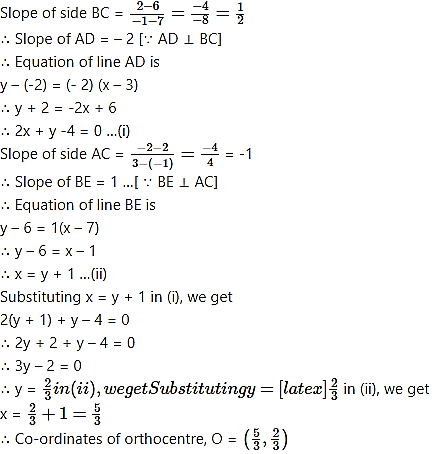
Question 9.
Show that the lines 3 – 4y + 5 = 0, lx – 8y + 5 = 0 and 4JC + 5y – 45 = 0 are concurrent. Find their point of concurrence.
Solution:
The number of lines intersecting at a point are called concurrent lines and their point of intersection is called the point of concurrence. Equations of the given lines are
3x – 4y + 5 = 0 …(i)
7x-8y + 5 = 0 …(ii)
4x + 5y – 45 = 0 …(iii)
By (i) x 2 – (ii), we get
– x + 5 = 0
∴ x = 5
Substituting x = 5 in (i), we get
3(5) – 4y + 5 = 0
∴ -4y = – 20
∴ y = 5
∴ The point of intersection of lines (i) and (ii) is given by (5, 5).
Substituting x = 5 and y = 5 in L.H.S. of (iii), we get
L.H.S. = 4(5) + 5(5) – 45
= 20 + 25 – 45
= 0
= R.H.S.
∴ Line (iii) also passes through (5, 5).
Hence, the given three lines are concurrent and the point of concurrence is (5, 5).
Question 10.
Find the equation of the line whose x-intercept is 3 and which ¡s perpendicular to the line 3x – y + 23 = 0.
Solution:
Slope of the line 3x – y + 23 = 0 is 3.
∴ Slope of the required line perpendicular to
Since the x-intercept of the required line is 3, it passes through (3, 0).
∴ The equation of the required line is ‘![]()
∴ 3y = x + 3
∴ x + 3y = 3
Question 11.
Find the distance of the origin from the line 7x + 24y – 50 = 0.
Solution:
Let p be the perpendicular distance of origin
fromtheline7x + 24y – 50 = 0
Here, a = 7, b = 24, c = -50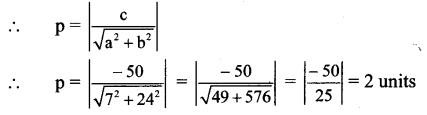
Question 12.
Find the distance of the point A(- 2, 3) from the line 12x – 5y – 13 = 0.
Solution:
Let p be the perpendicular distance of the point A(- 2, 3) from the line 12x – 5y – 13 = 0
Here, a = 12, b = – 5, c = – 13, = -2, = 3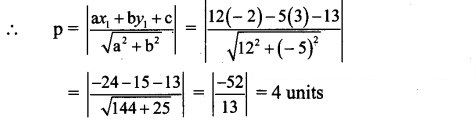
Question 13.
Find the distance between parallel lines 4x – 3y + 5 = 0 and 4xr – 3y + 7 = 0.
Solution:
Equations of the given parallel lines are 4x – 3y + 5 = 0 and 4x – 3y + 1 = 0
Here, a = 4, b = – 3, = 5 and = 7
∴ Distance between the parallel lines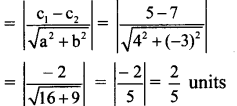
Question 14.
Find the distance between the parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0.
Solution:
Equations of the given parallel lines are 3x + 2y + 6 = 0 and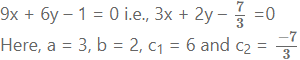
∴ Distance between the parallel lines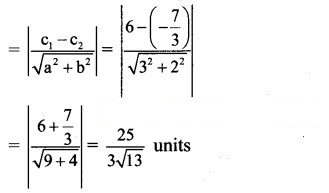
Question 15.
Find the points on the line x + y – 4 = 0 which are at a unit distance from the line 4JC + 3y = 10.
Solution:
Let P(, ) be a point on the line x + y – 4 = o.
∴ + – 4 = 0
∴ = 4 – x1 …(i)
Also, distance of P from the line 4x + 3y- 10 = 0 is 1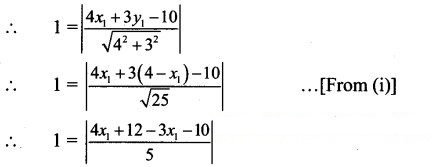
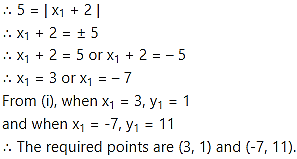
[Note: The question has been modified]
Question 16.
Find the equation of the line parallel to the X-axis and passing through the point of intersection of lines x + y – 2 = 0 and 4x + 3y = 10.
Solution:
Let u = x + y – 2 = 0 and v = 4x + 3y – 10 = 0
Equation of the line passing through the point of intersection of lines u = 0 and v = 0 is given by u + kv = 0.
∴ (x + y – 2) + k(4x + 3y – 10) = 0 …(i)
∴ x + y – 2 + 4kx + 3ky – 10k = 0
∴ x + 4kx + y + 3ky – 2 – 10k = 0
∴ (1+ 4k)x + (1 + 3k)y – 2 – 10k = 0
But, this line is parallel to X-axis.
∴ Its slope = 0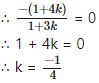
Substituting the value of k in (i), we get
(x + y – 2) + (4x + 3y – 10) = 0
∴ 4(x +y – 2) – (4x + 3y -10 ) = 0
∴ 4x + 4y – 8 – 4x – 3y + 10 = 0
∴ y + 2 = 0, which is the equation of the required line.
[Note: Answer given in the textbook is 5y – 8= 0. However, as per our calculation it is y + 2 = 0.]
Question 17.
Find the equation of the line passing through the point of intersection of lines x + y – 2 = 0 and 2xr – 3y + 4 = 0 and making intercept 3 on the X-axis.
Solution:
Let u ≡ x + y – 2 = 0 and v ≡ 2x – 3y + 4 = 0
Equation of the line passing through the point of intersection of lines u = 0 and v = 0 is given by u + kv = 0.
∴ (x +y – 2) + k(2x – 3y + 4) = 0 …(i)
But, x-intercept of line is 3.
∴ It passes through (3, 0).
Substituting x = 3 and y = 0 in (i), we get
(3 + 0 – 2) + k(6 – 0 + 4) = 0
∴ 1 + 10k = 0
∴ 10(x + y – 2) – (2x – 3y + 4) = 0
∴ 10x + 10y -20 — 2x + 3y-4 = 0
∴ 8x + 13y – 24 = 0, which is the equation of the required line.
Question 18.
If A(4, 3), B(0, 0) and C(2, 3) are the vertices of ΔABC, then find the equation of bisector of angle BAC.
Solution:
Let the bisector of ∠ BAC meets BC at point D.
∴ Point D divides seg BC in the ratio l(AB) : l(AC)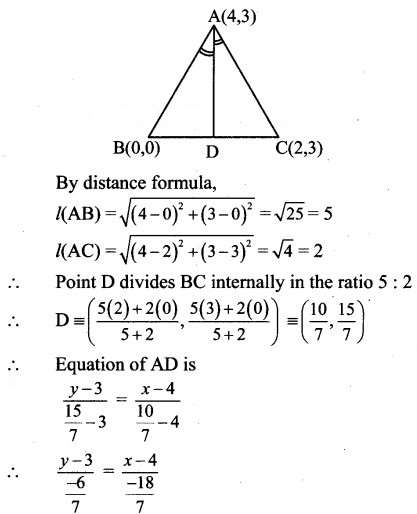
∴ 18 (y – 3) = 6 (x – 4)
∴ 3(y – 3) = x – 4
∴ 3y – 9 = x – 4
∴ x – 3y + 5 = 0
Question 19.
D(- 1, 8), E(4, – 2), F(- 5, – 3) are midpoints of sides BC, CA and AB of AABC. Find
i. equations of sides of ΔABC.
ii. co-ordinates of the circumcentre of ΔABC.
Solution:
Let A(), B() and C() be the vertices of ΔABC.
Given, points D, E and F are midpoints of sides BC, CA and AB respectively of ΔABC.
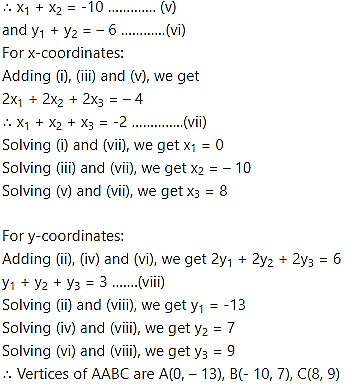

∴ 8(y + 13) = 22x
∴ 4(y + 13) = 11x
∴ 11x – 4y – 52 = 0
ii. Here, A(0, – 13), B(- 10, 7), C(8, 9) are the vertices of ΔABC.
Let F be the circumcentre of AABC.
Let FD and FE be perpendicular bisectors of the sides BC and AC respectively.
D and E are the midpoints of side BC and AC.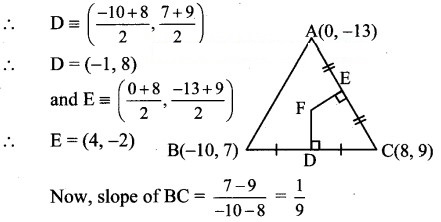

Question 20.
0(0, 0), A(6, 0) and B(0, 8) are vertices of a triangle. Find the co-ordinates of the incentre of ∆OAB.
Solution:
Let bisector of ∠O meet AB at point D and bisector of ∠A meet BO at point E
∴ Point D divides seg AB in the ratio l(OA): l(OB)
and point E divides seg BO in the ratio l(AB): l(AO)
Let I be the incentre of ∠OAB.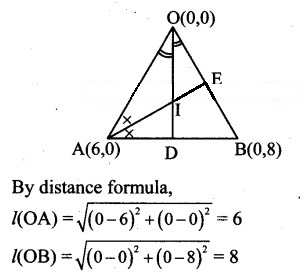
∴ Point D divides AB internally in 6 : 8
i.e. 3 :4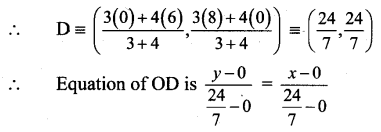
∴ y = x …(i)
Now, by distance formula,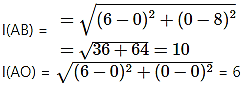
∴ Point E divides BO internally in 10 : 6 i.e. 5:3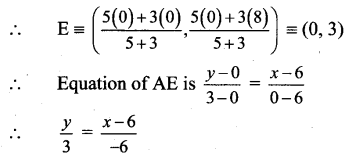
∴ -2y = x – 6
∴ x + 2y = 6 …(ii)
To find co-ordinates of incentre, we have to solve equations (i) and (ii).
Substituting y = x in (ii), we get
x + 2x = 6
∴ x = 2
Substituting the value of x in (i), we get
y = 2
∴ Co-ordinates of incentre I ≡ (2, 2).
Alternate Method:
Let I be the incentre.
I lies in the 1st quadrant.
OPIR is a square having side length r.
Since OA = 6, OP = r,
PA = 6 – r
Since PA = AQ,
AQ = 6 – r …(i)
Since OB = 8, OR = r,
BR = 8 – r
∴ BR = BQ
∴ BQ = 8 – r …(ii)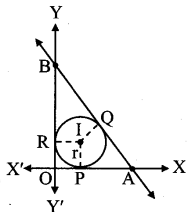
AB = BQ + AQ
∴ BQ + AQ= 10
∴ (8 – r) + (6 – r) = 10
∴ 2r = 14- 10 = 4
∴ r = 2
∴ I = (2,2)
