Question 1.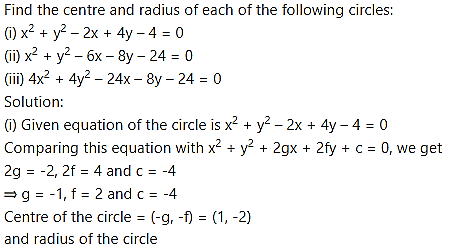
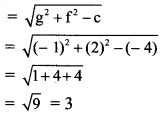
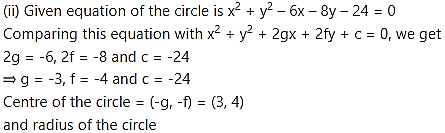
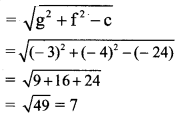
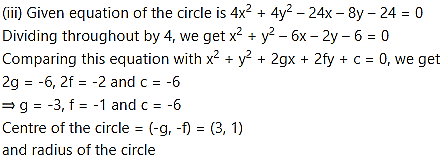
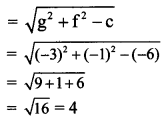
Question 2.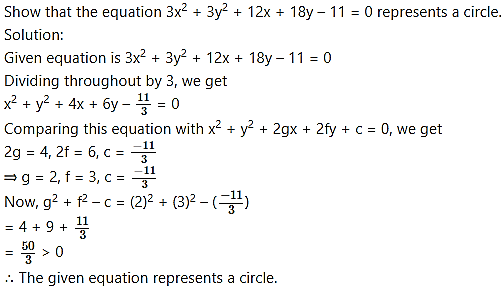
Question 3.
Find the equation of the circle passing through the points (5, 7), (6, 6), and (2, -2).
Solution:
Let C(h, k) be the centre of the required circle.
Since the required circle passes through points A(5, 7), B(6, 6), and D(2, -2),
CA = CB = CD = radius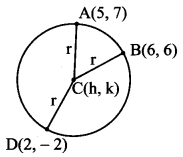

Substituting k = 3 in (i), we get
h + 3(3) – 11 = 0
⇒ h + 9 – 11 = 0
⇒ h = 2
Centre of the circle is C(2, 3).
radius (r) = CD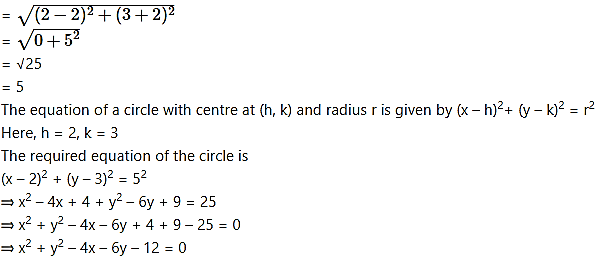
Question 4.
Show that the points (3, -2), (1, 0), (-1, -2) and (1, -4) are concyclic.
Solution:
Let the equation of the circle passing through the points (3, -2), (1, 0) and (-1, -2) be![]()
For point (3, -2),
Substituting x = 3 and y = -2 in (i), we get
9 + 4 + 6g – 4f + c = 0
⇒ 6g – 4f + c = -13 ….(ii)
For point (1, 0),
Substituting x = 1 andy = 0 in (i), we get
1 + 0 + 2g + 0 + c = 0
⇒ 2g + c = -1 ……(iii)
For point (-1, -2),
Substituting x = -1 and y = -2, we get
1 + 4 – 2g – 4f + c = 0
⇒ 2g + 4f – c = 5 …….(iv)
Adding (ii) and (iv), we get
8g = -8
⇒ g = -1
Substituting g = -1 in (iii), we get
-2 + c = -1
⇒ c = 1
Substituting g = -1 and c = 1 in (iv), we get
-2 + 4f – 1 = 5
⇒ 4f = 8
⇒ f = 2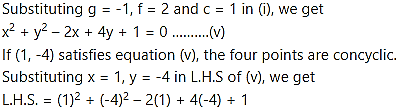
= 1 + 16 – 2 – 16 + 1
= 0
= R.H.S.
Point (1, -4) satisfies equation (v).
∴ The given points are concyclic.
