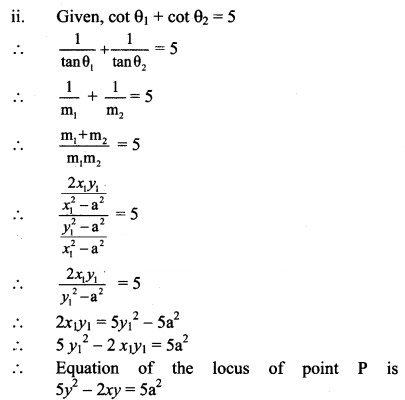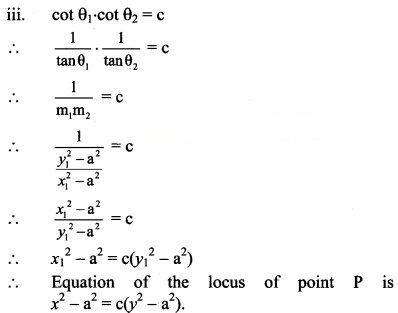Maharashtra Board Class 11 Maths Part 1 Chapter 6 Circle Miscellaneous Exercise 6 Solution

(I) Choose the correct alternative.

Question 1.
Equation of a circle which passes through (3, 6) and touches the axes is

Question 2.
If the lines 2x – 3y = 5 and 3x – 4y = 7 are the diameters of a circle of area 154 sq. units, then find the equation of the circle.

Question 3.
Find the equation of the circle which passes through the points (2, 3) and (4, 5), and the center lies on the straight line y – 4x + 3 = 0.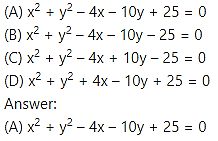

Question 4.
The equation(s) of the tangent(s) to the circle x² + y² = 4 which are parallel to x + 2y + 3 = 0 are
(A) x – 2y = 2
(B) x + 2y = ±2√3
(C) x + 2y = ±2√5
(D) x – 2y = ±2√5
Answer:
(C) x + 2y = ±2√5

Question 5.
If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to a circle, then find the radius of the circle.

Hint:
Tangents are parallel to each other.
The perpendicular distance between tangents = diameter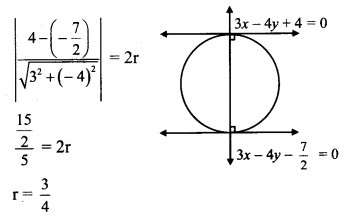

Question 6.
The area of the circle having centre at (1, 2) and passing through (4, 6) is
(A) 5π
(B) 10π
(C) 25π
(D) 100π
Answer:
(C) 25π
Hint: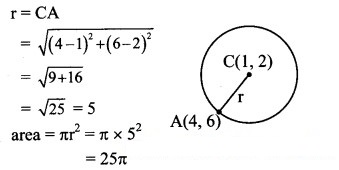

Question 7.
If a circle passes through the points (0, 0), (a, 0), and (0, b), then find the co-ordinates of its centre.

Question 9.
A pair of tangents are drawn to a unit circle with centre at the origin and these tangents intersect at A enclosing an angle of 60. The area enclosed by these tangents and the arc of the circle is

Hint: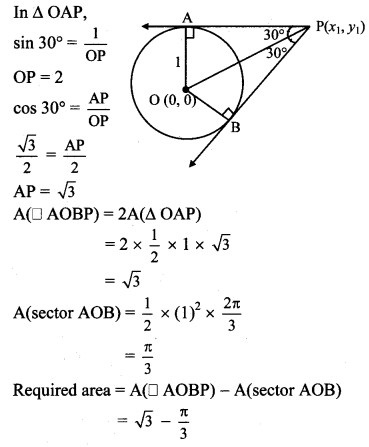

Question 10.

(II) Answer the following:

Question 1.

and radius of the circle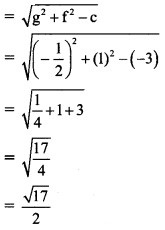

Question 2.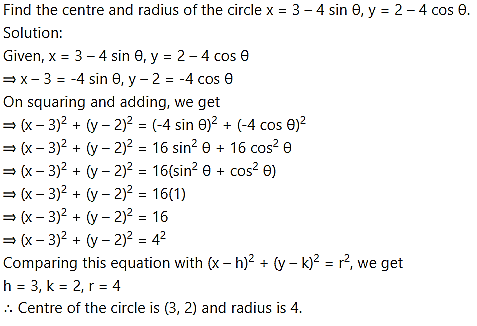

Question 3.
Find the equation of circle passing through the point of intersection of the lines x + 3y = 0 and 2x – 7y = 0 and whose centre is the point of intersection of lines x + y + 1 = 0 and x – 2y + 4 = 0.
Solution:
Required circle passes through the point of intersection of the lines x + 3y = 0 and 2x – 7y = 0.
x + 3y = 0
⇒ x = -3y ……..(i)
2x – 7y = 0 ……(ii)
Substituting x = -3y in (ii), we get
⇒ 2(-3y) – 7y = 0
⇒ -6y – 7y = 0
⇒ -13y = 0
⇒ y = 0
Substituting y = 0 in (i), we get
x = -3(0) = 0
Point of intersection is O(0, 0).
This point O(0, 0) lies on the circle.
Let C(h, k) be the centre of the required circle.
Since, point of intersection of lines x + y = -1 and x – 2y = -4 is the centre of circle.
∴ x = h, y = k
∴ Equations of lines become
h + k = -1 ……(iii)
h – 2k = -4 …..(iv)
By (iii) – (iv), we get
3k = 3
⇒ k = 1
Substituting k = 1 in (iii), we get
h + 1 = -1
⇒ h = -2
∴ Centre of the circle is C(-2, 1) and it passes through point O(0, 0).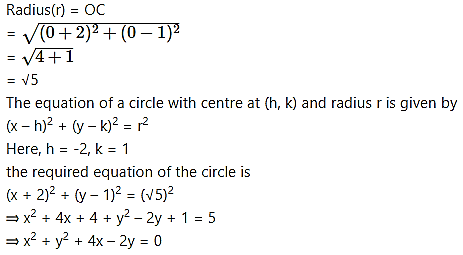

Question 4.
Find the equation of the circle which passes through the origin and cuts off chords of lengths 4 and 6 on the positive side of the X-axis and Y-axis respectively.
Solution: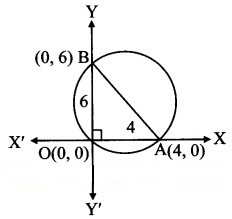

Let the circle cut the chord of length 4 on X-axis at point A and the chord of length 6 on the Y-axis at point B.
∴ the co-ordinates of point A are (4, 0) and co-ordinates of point B are (0, 6).
Since ∠BOA is a right angle.
AB represents the diameter of the circle.

Question 5.
Show that the points (9, 1), (7, 9), (-2, 12) and (6, 10) are concyclic.
Solution:
Let the equation of circle passing through the points (9, 1), (7, 9), (-2, 12) be
 + 2gx + 2fy + c = 0 …….(i)
For point (9, 1),
Substituting x = 9 andy = 1 in (i), we get
81 + 1 + 18g + 2f + c = 0
⇒ 18g + 2f + c = -82 …..(ii)
For point (7, 9),
Substituting x = 7 andy = 9 in (i), we get
49 + 81 + 14g + 18f + c = 0
⇒ 14g + 18f + c = -130 ……(iii)
For point (-2, 12),
Substituting x = -2 and y = 12 in (i), we get
4 + 144 – 4g + 24f + c = 0
⇒ -4g + 24f + c = -148 …..(iv)
By (ii) – (iii), we get
4g – 16f = 48
⇒ g – 4f = 12 …..(v)
By (iii) – (iv), we get
18g – 6f = 18
⇒ 3g – f = 3 ……(vi)
By 3 × (v) – (vi), we get
-11f = 33
⇒ f = -3
Substituting f = -3 in (vi), we get
3g – (-3) = 3
⇒ 3g + 3 = 3
⇒ g = 0
Substituting g = 0 and f = -3 in (ii), we get
18(0) + 2(-3) + c = – 82
⇒ -6 + c = -82
⇒ c = -76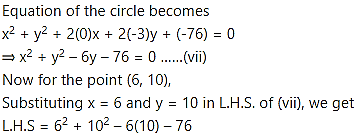

= 36 + 100 – 60 – 76
= 0
= R.H.S.
∴ Point (6,10) satisfies equation (vii).
∴ the given points are concyciic.

Question 6.

When x = -5,
y = -10 + 6 = -4
∴ Point of intersection in B (-5, -4).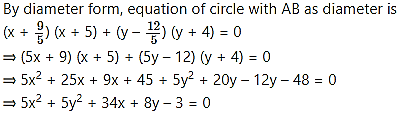

Question 7.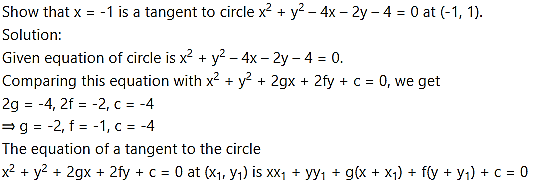

the equation of the tangent at (-1, 1) is
⇒ x(-1) + y(1) – 2(x – 1) – 1(y + 1) – 4 = 0
⇒ -3x – 3 = 0
⇒ -x – 1 = 0
⇒ x = -1
∴ x = -1 is the tangent to the given circle at (-1, 1).

Question 8.

Question 9.
Find the equation of locus of the point of intersection of perpendicular tangents drawn to the circle x = 5 cos θ and y = 5 sin θ.
Solution:
The locus of the point of intersection of perpendicular tangents is the director circle of the given circle.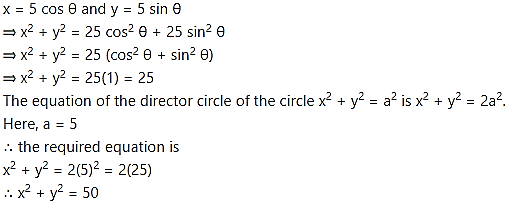

Question 10.

Question 11.
Find the lengths of the intercepts made on the co-ordinate axes, by the circles.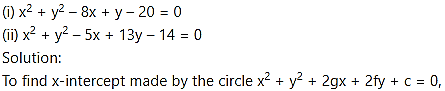

substitute y = 0 and get a quadratic equation in x, whose roots are, say, x₁ and x₂.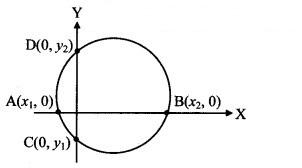

These values represent the abscissae of ends A and B of the x-intercept.

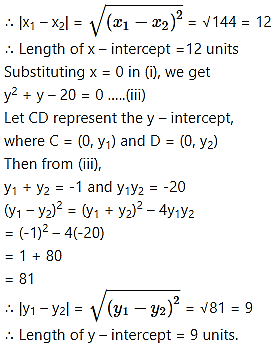
Alternate Method: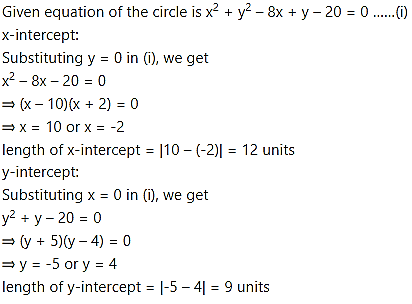

(ii) Given equation of the circle is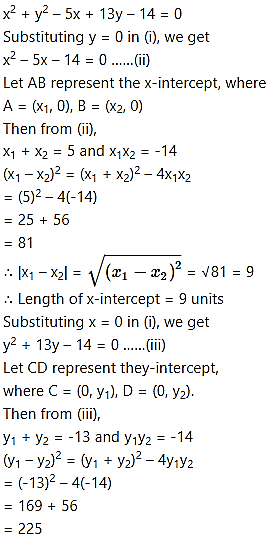


∴ Length ofy-intercept = 15 units

Question 12.
Show that the circles touch each other externally. Find their point of contact and the equation of their common tangent.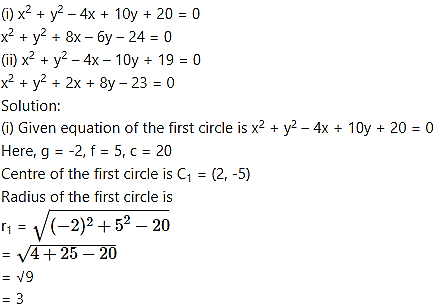





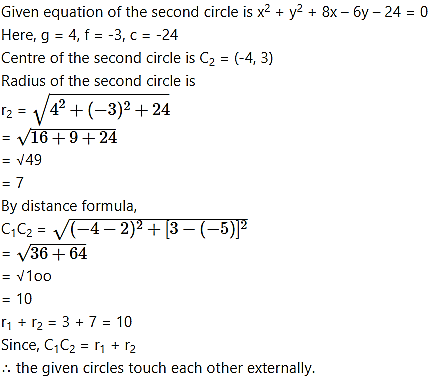
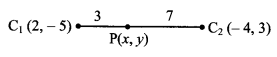
Equation of common tangent is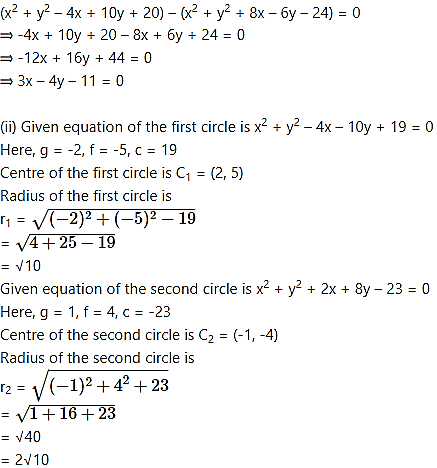

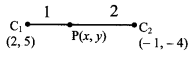
∴ P divides C₁ C₂ internally in the ratio r₁ : r₂ i.e. 1 : 2
∴ By internal division,

Point of contact = (1, 2)
Equation of common tangent is
( – 4x – 10y + 19) – ( + 2x + 8y – 23) = 0
⇒ -4x – 10y + 19 – 2x – 8y + 23 = 0
⇒ -6x – 18y + 42 = 0
⇒ x + 3y – 7 = 0

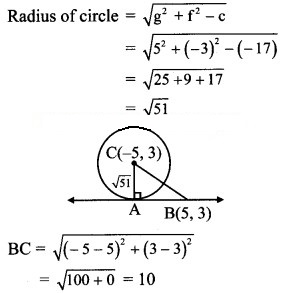
Question 13.
Show that the circles touch each other internally. Find their point of contact and the equation of their common tangent.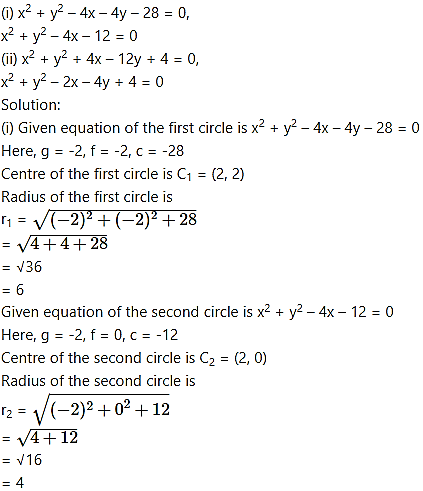

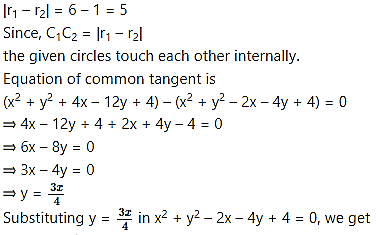
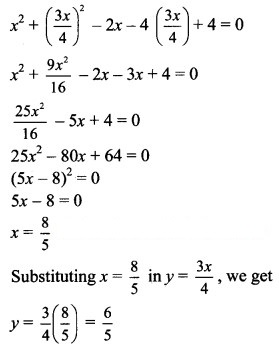
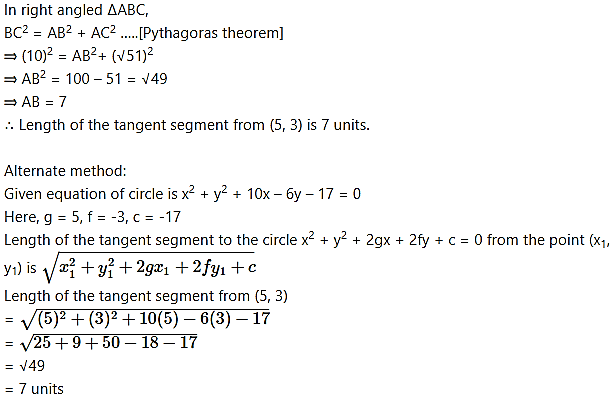
Question 15.

Question 16.

Question 18.

Question 19.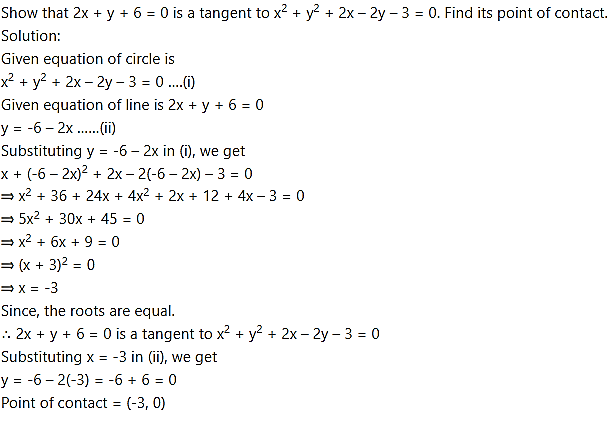

Question 20.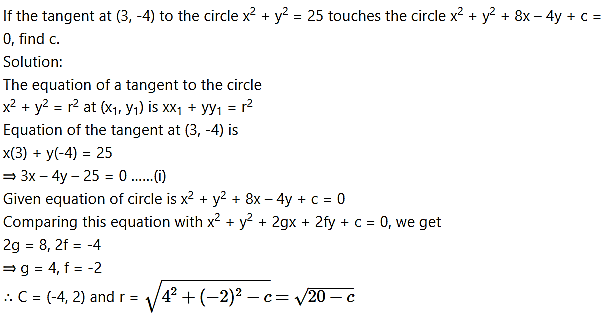

Since line (i) is a tangent to this circle also, the perpendicular distance from C(-4, 2) to line (i) is equal to radius r.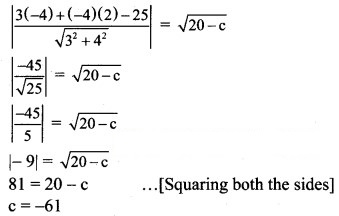

Question 21.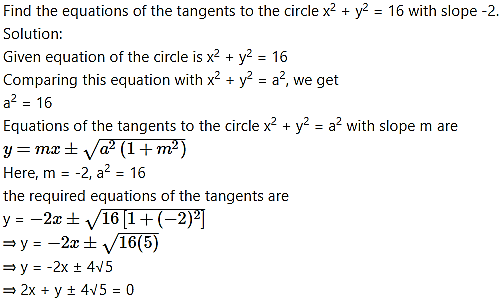

Question 22.

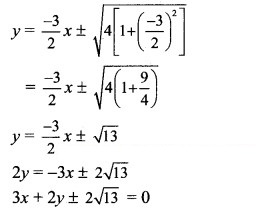
Question 23.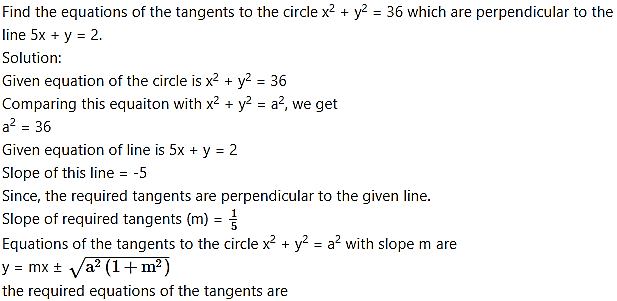

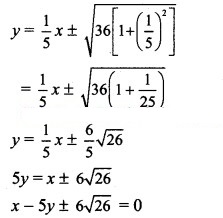
Question 24.

Question 25.

Alternate method: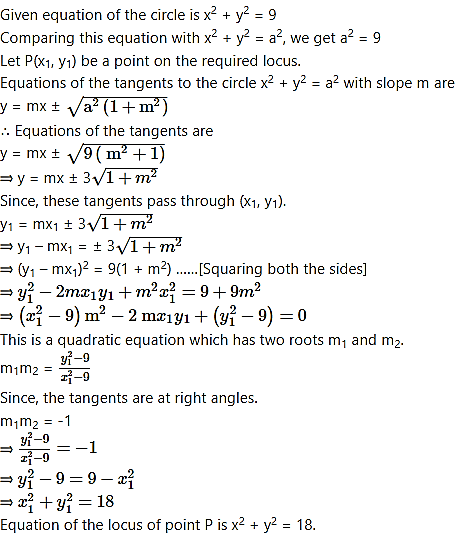

Question 26.