Question 1.
If odds in favour of X solving a problem are 4 : 3 and odds against Y solving the same problem are 2 : 3. Find the probability of:
(i) X solving the problem
(ii) Y solving the problem
Solution:
(i) Odds in favour of X solving a problem are 4 : 3.
∴ The probability of X solving the problem is
Question 2.
The odds against John solving a problem are 4 to 3 and the odds in favour of Rafi solving the same problem are 7 to 5. What is the chance that the problem is solved when both of them try it?
Solution:

Question 3.
The odds against student X solving a statistics problem are 8 : 6 and odds in favour of student Y solving the same problem are 14 : 16. Find the chance that
(i) the problem will be solved if they try it independently.
(ii) neither of them solves the problem.
Solution:
(ii) Required probability = P(X’ ∩ Y’)
Since X and Y are independent events, X’ and Y’ are also independent events.
∴ Required probability = P(X’) . P(Y’)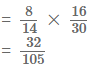
Question 4.
The odds against a husband who is 60 years old, living till he is 85 are 7 : 5. The odds against his wife who is now 56, living till she is 81 are 5 : 3. Find the probability that
(i) at least one of them will be alive 25 years hence.
(ii) exactly one of them will be alive 25 years hence.
Solution:

Question 5.
There are three events A, B, and C, one of which must, and only one can happen. The odds against event A are 7 : 4 and odds against event B are 5 : 3. Find the odds against event C.
Solution:
Question 6.
In a single toss of a fair die, what are the odds against the event that number 3 or 4 turns up?
Solution:
When a fair die is tossed, the sample space is
S = {1, 2, 3, 4, 5, 6}
∴ n(S) = 6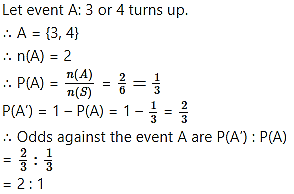
Question 7.
The odds in favour of A winning a game of chess against B are 3 : 2. If three games are to be played, what are the odds in favour of A’s winning at least two games out of the three?
Solution:
Let event A: A wins the game and event B: B wins the game.
Since the odds in favour of A winning a game against B are 3 : 2,
the probability of occurrence of event A and B is given by![]()
Let event E: A wins at least two games out of three games.
∴ P(E) = P(A) . P(A) . P(B) + P(A) . P(B) . P(A) + P(B) . P(A) . P(A) + P(A) . P(A) . P(A)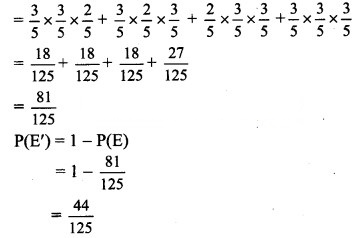
∴ Odds in favour of A’s winning at least two games out of three are P(E) : P(E’)![]()
= 81 : 44
