Maharashtra Board Class 11 Maths Part 2 Chapter 1 Complex Numbers Ex 1.1 Solution

Chapter 1 Complex Numbers Ex 1.1

Question 1.
Simplify:
(i) √-16 + 3√-25 + √-36 – √-625
Solution: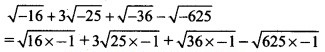

= 4i + 3(5i) + 6i – 25i
= 25i – 25i
= 0

(ii) 4√-4 + 5√-9 – 3√-16
Solution: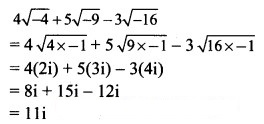

Question 2.
Write the conjugates of the following complex numbers
(i) 3 + i
Solution:
Conjugate of (3 + i) is (3 – i).

(ii) 3 – i
Solution:
Conjugate of (3 – i) is (3 + i).

(iii) √-5 – √7 i
Solution:
Conjugate of (√-5 – √7 i) is (√-5 + √7 i).

(iv) -√-5
Solution:
-√-5 = -√5 × √-1 = -√5 i
Conjugate of (-√-5) is √5 i

(v) 5i
Solution:
Conjugate of (5i) is (-5i).

(vi) √5 – i
Solution:
Conjugate of (√5 – i) is (√5 + i).

(vii) √2 + √3 i
Solution:
Conjugate of (√2 + √3 i) is (√2 – √3 i)

(viii) cos θ + i sin θ
Solution:
Conjugate of (cos θ + i sin θ) is (cos θ – i sin θ)

Question 3.
Find a and b if
(i) a + 2b + 2ai = 4 + 6i
Solution:
a + 2b + 2ai = 4 + 6i
Equating real and imaginary parts, we get
a + 2b = 4 …..(i)
2a = 6 ……(ii)
∴ a = 3
Substituting, a = 3 in (i), we get
3 + 2b = 4
∴ b = 1/2
∴ a = 3 and b = 

Check:
For a = 3 and b = 1/2
Consider, L.H.S. = a + 2b + 2ai
= 3 + 2(1/2) + 2(3)i
= 4 + 6i
= R.H.S.

(ii) (a – b) + (a + b)i = a + 5i
Solution:
(a – b) + (a + b)i = a + 5i
Equating real and imaginary parts, we get
a – b = a ……(i)
a + b = 5 ……(ii)
From (i), b = 0
Substituting b = 0 in (ii), we get
a + 0 = 5
∴ a = 5
∴ a = 5 and b = 0

(iii) (a + b) (2 + i) = b + 1 + (10 + 2a)i
Solution:
(a + b) (2 + i) = b + 1 + (10 + 2a)i
2(a + b) + (a + b)i = (b + 1) + (10 + 2a)i
Equating real and imaginary parts, we get
2(a + b) = b + 1
∴ 2a + b = 1 ……(i)
and a + b = 10 + 2a
-a + b = 10 …….(ii)
Subtracting equation (ii) from (i), we get
3a = -9
∴ a = -3
Substituting a = – 3 in (ii), we get
-(-3) + b = 10
∴ b = 7
∴ a = -3 and b = 7

(iv) abi = 3a – b + 12i
Solution:
abi = 3a – b + 12i
∴ 0 + abi = (3a – b) + 12i
Equating real and imaginary parts, we get
3a – b = 0
∴ 3a = b …..(i)
and ab = 12
∴ b =  ……..(ii)
Substituting b =  in (i), we get
3a = 
3a² = 12
a² = 4
a = ±2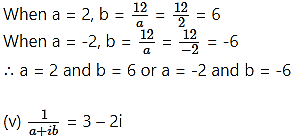

Solution: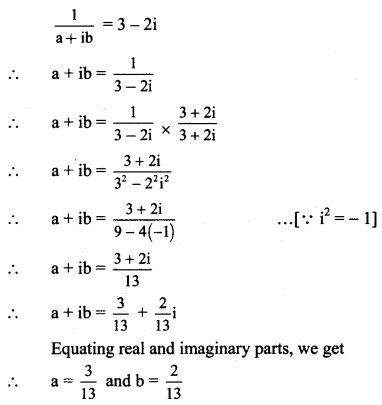

(vi) (a + ib) (1 + i) = 2 + i
Solution:
(a + ib)(1 + i) = 2 + i
a + ai + bi + bi² = 2 + i
a + (a + b)i + b(-1) = 2 + i ……(∵ i² = -1)
(a – b) + (a + b)i = 2 + i
Equating real and imaginary parts, we get
a – b = 2 ……(i)
a + b = 1 …….(ii)
Adding equations (i) and (ii), we get
2a = 3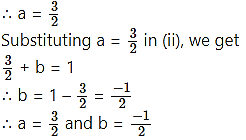

Question 4.
Express the following in the form of a + ib, a, b ∈ R, i = √-1. State the values of a and b:
(i) (1 + 2i)(-2 + i)
Solution:
(1 + 2i)(-2 + i) = -2 + i – 4i + 2
= -2 – 3i + 2(-1) ……[∵ i² = -1]
∴ (1 + 2i)(-2 + i) = -4 – 3i
∴ a = -4 and b = -3

(ii) (1 + i)(1 – i)-1
Solution: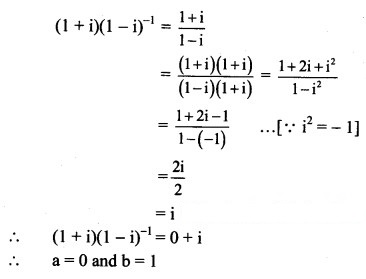

Solution:

Solution: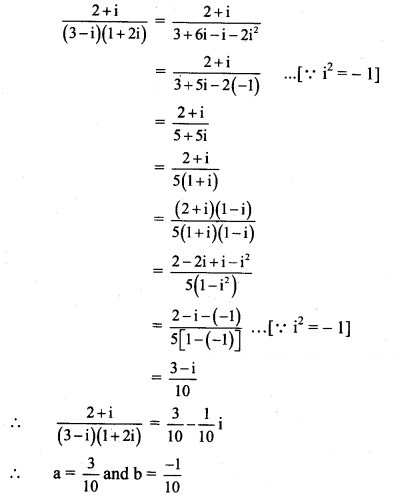

Solution: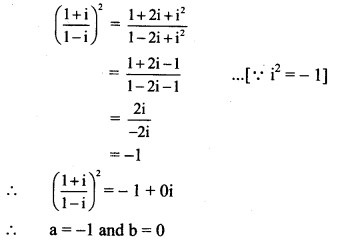

Solution: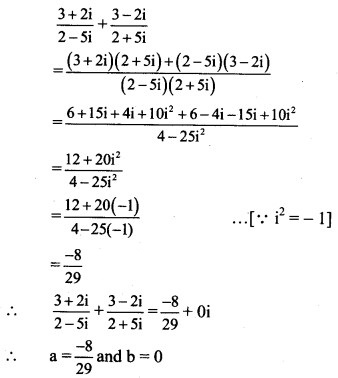

(vii) (1 + i
Solution: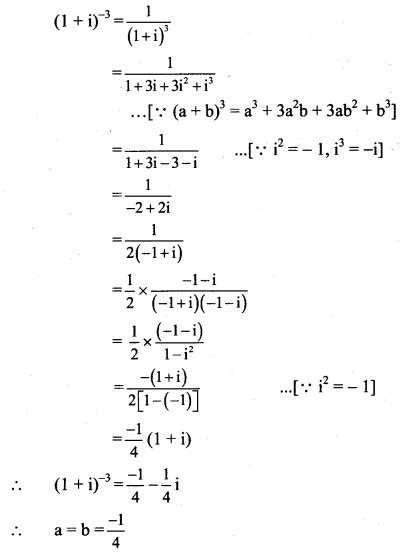

Solution: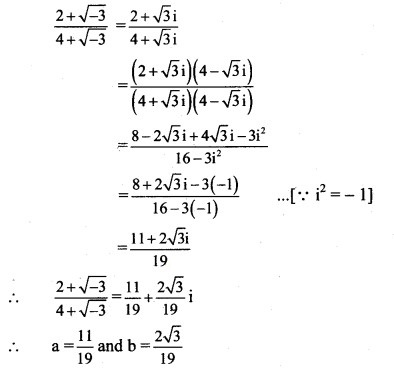

(ix) (-√5 + 2√-4 ) + (1 – √-9 ) + (2 + 3i)(2 – 3i)
Solution:
(-√5 + 2√-4) + (1 – √-9) + (2 + 3i)(2 – 3i)
= (-√5 + 2√4.√-1) + (1 – √9.√-1) + 4 – 9
= [-√5 + 2(2)i] + (1 – 3i) + 4 – 9
= -√5 + 4i + 1 – 3i + 4 – 9(-1) ……[∵  = -1]
= (14 – √5) + i
∴ a = 14 – √5 and b = 1

(x) (2 + 3i)(2 – 3i)
Solution:
(2 + 3i)(2 – 3i)
= 4 – 9
= 4 – 9(-1) …[∵  = -1]
= 4 + 9
= 13
∴ (2 + 3i)(2 – 3i) = 13 + 0i
∴ a = 13 and b = 0

Solution:

Question 5.
Show that (-1 + √3i is a real number.
Solution: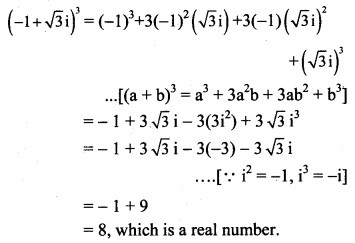

Question 6.

Solution: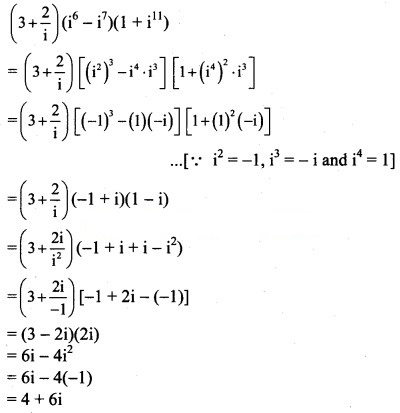

Question 7.
Evaluate the following:

Solution: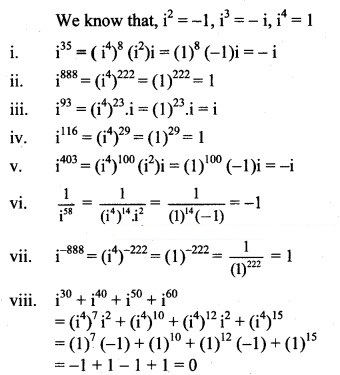

Question 8.

Solution: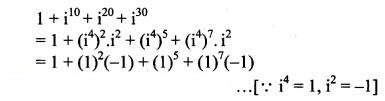

= 1 – 1 + 1 – 1
= 0, which is a real number.

Question 9.
Find the value of

Solution: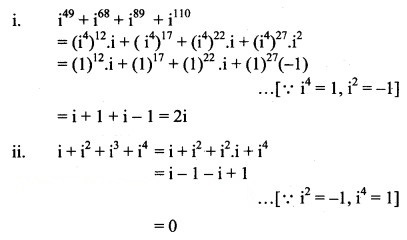

Question 10.

Solution:

Question 11.

Solution: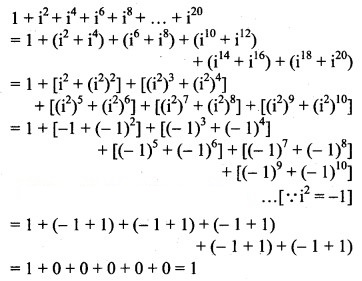

Question 12.

Solution: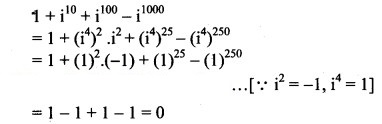

Question 13.
Is (1 + ) a real number? Justify your answer.
Solution: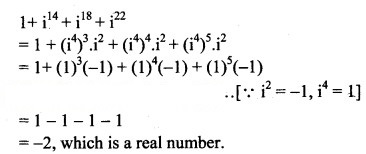

Question 14.

Solution: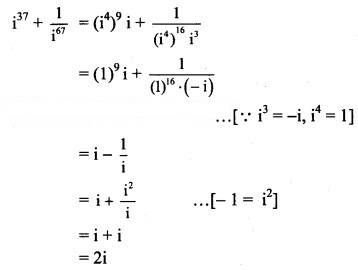

Question 15.

Solution:

Question 16.

Solution:

Question 17.

Solution:

Question 18.

Alternate Method:

Consider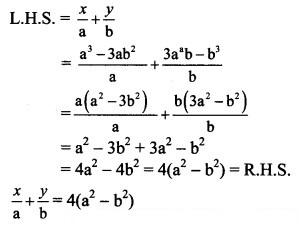

Question 19.

a + 3i = (1 – i)(2 + ib)
= 2 + bi – 2i – bi²
= 2 + (b – 2)i – b(-1) ……[∵ i² = -1]
a + 3i = (2 + b) + (b – 2)i
Equating real and imaginary parts, we get
a = 2 + b and 3 = b – 2
a = 2 + b and b = 5
a = 2 + 5 = 7
5a – 7b = 5(7) – 7(5) = 35 – 35 = 0

Question 20.

Solution: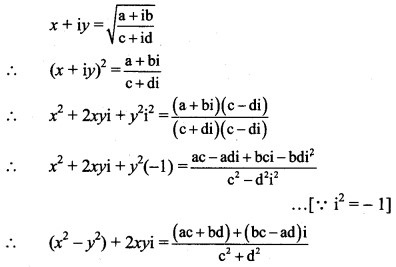

Question 21.

Solution: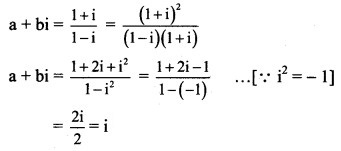

∴ a + bi = 0 + i
Equating real and imaginary parts, we get
a = 0 and b = 1

Question 22.

Solution: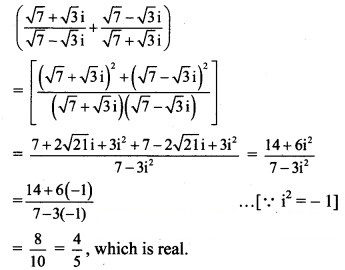

Question 23.

Solution: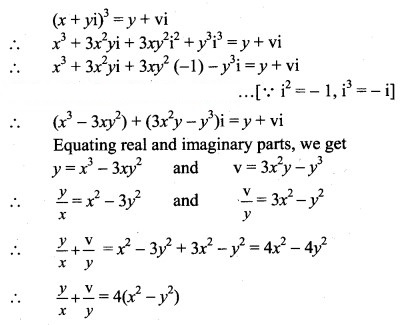

Question 24.
Find the values of x and y which satisfy the following equations (x, y ∈ R)
(i) (x + 2y) + (2x – 3y)i + 4i = 5
Solution:
(x + 2y) + (2x – 3y)i + 4i = 5
(x + 2y) + (2x – 3y)i = 5 – 4i
Equating real and imaginary parts, we get
x + 2y = 5 ……(i)
and 2x – 3y = -4 …..(ii)
Equation (i) x 2 – equation (ii) gives
7y = 14
∴ y = 2
Substituting y = 2 in (i), we get
x + 2(2) = 5
x + 4 = 5
∴ x = 1
∴ x = 1 and y = 2

Check:
For x = 1 and y = 2
Consider, L.H.S. = (x + 2y) + (2x – 3y)i + 4i
= (1 + 4) + (2 – 6)i + 4i
= 5 – 4i + 4i
= 5
= R.H.S.

Solution:

(x + y) + (y – x – 2)i = 2i
(x + y) + (y – x – 2)i = 0 + 2i
Equating real and imaginary parts, we get
x + y = 0 and y – x – 2 = 2
∴ x + y = 0 …….(i)
and -x + y = 4 …….(ii)
Adding (i) and (ii), we get
2y = 4
∴ y = 2
Substituting y = 2 in (i), we get
x + 2 = 0
∴ x = -2
∴ x = -2 and y = 2

Solution: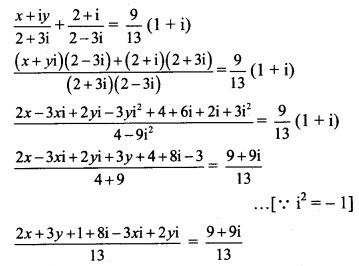

(2x + 3y + 1) + (8 – 3x + 2y)i = 9 + 9i
Equating real and imaginary parts, we get
2x + 3y + 1 = 9 and 8 – 3x + 2y = 9
2x + 3y = 8 ……(i)
and 3x – 2y = – 1 ……(ii)
Equation (i) × 2 + equation (ii) × 3 gives
13x = 13
∴ x = 1
Substituting x = 1 in (i), we get
2(1) + 3y = 8
3y = 6
∴ y = 2
∴ x = 1 and y = 2

(iv) If x(1 + 3i) + y(2 – i) – 5 +  = 0, find x + y
Solution:
x(1 + 3i) + y(2 – i) – 5 +  = 0
x + 3xi + 2y – yi – 5 – i = 0 ……[∵  = -i]
(x + 2y – 5) + (3x – y – 1)i = 0 + 0i
Equating real and imaginary parts, we get
x + 2y – 5 = 0 …..(i)
and 3x – y – 1 = 0 ……(ii)
Equation (i) + equation (ii) × 2 gives
7x – 7 = 0
7x = 1
∴ x = 1
Substituting x = 1 in (i), we get
1 + 2y – 5 = 0
2y = 4
y = 2
∴ x = 1 and y = 2
∴ x + y = 1 + 2 = 3

(v) If x + 2i + 15y = 7x + i³(y + 4), find x + y
Solution: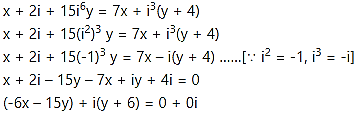

Equating real and imaginary parts, we get
-6x – 15y = 0 and y + 6 = 0
-6x – 15y = 0 and y = -6
-6x – 15(-6) = 0
-6x + 90 = 0
∴ x = 15
∴ x + y = 15 – 6 = 9