Question 1.
Determine whether the sum to infinity of the following G.P.s exist, if exists find them.
Solution: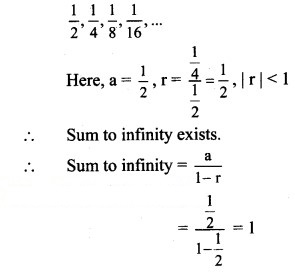
Solution:
Solution: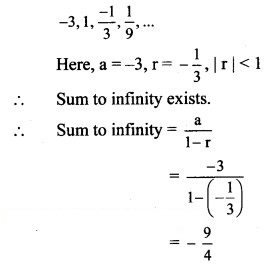
Solution: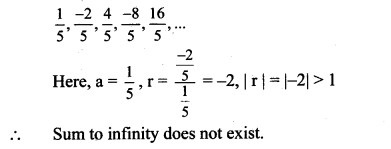
(v) 9, 8.1, 7.29, ……
Solution:
9, 8.1, 7.29, …..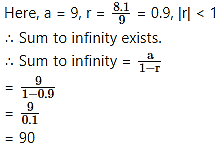
Question 2.
Express the following recurring decimals as rational numbers.
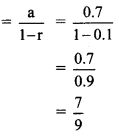
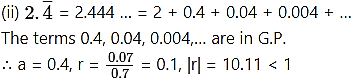
∴ Sum to infinity exists.
∴ Sum to infinity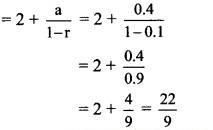
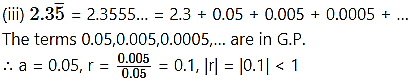
∴ Sum to infinity exists.
∴ Sum to infinity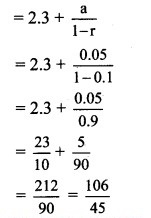
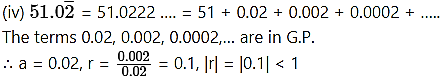
∴ Sum to infinity exists.
∴ Sum to infinity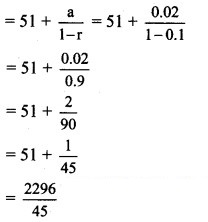
Question 3.
If the common ratio of a G.P. is 2/3 and the sum to infinity is 12, find the first term.
Solution: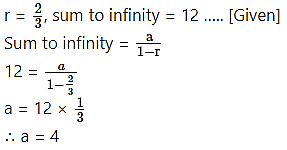
Question 4.
If the first term of the G.P. is 6 and its sum to infinity is 96/17, find the common ratio.
Solution:
a = 6, sum to infinity = 96/17 …..[Given]
Sum to infinity = a/1-r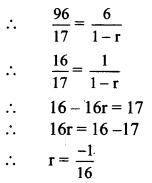
Question 5.
The sum of an infinite G.P. is 5 and the sum of the squares of these terms is 15, find the G.P.
Solution:
Let the required G.P. be a, ar, , , …..
Sum to infinity of this G.P. = 5
Question 6.
Find
Solution: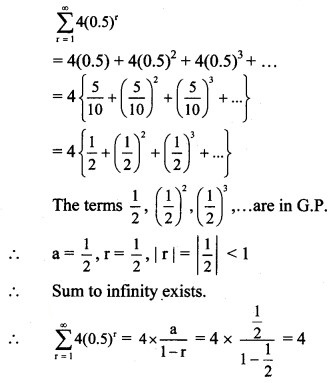
Solution: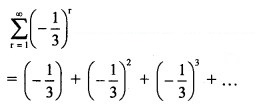
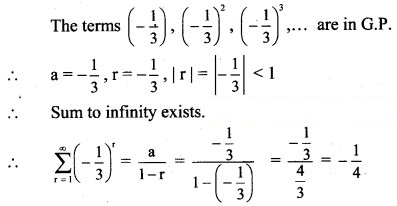
Solution:
Solution: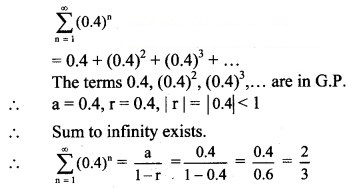
Question 7.
The midpoints of the sides of a square of side 1 are joined to form a new square. This procedure is repeated indefinitely. Find the sum of
(i) the areas of all the squares.
(ii) the perimeters of all the squares.
Solution: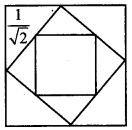
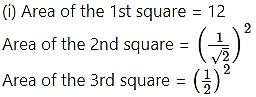
and so on.
∴ Sum of the areas of all the squares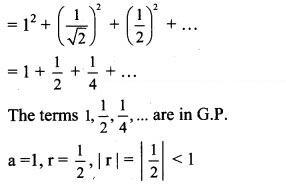
∴ Sum to infinity exists.![]()
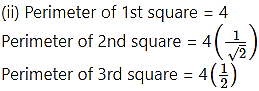
and so on.
Sum of the perimeters of all the squares
Question 8.
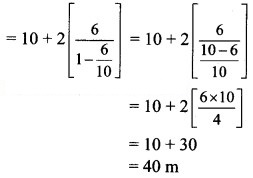
A ball is dropped from a height of 10 m. It bounces to a height of 6m, then 3.6 m, and so on. Find the total distance travelled by the ball.
Solution:
Here, on the first bounce, the ball will go 6 m and it will return 6 m.
On the second bounce, the ball will go 3.6 m and it will return 3.6 m, and so on.
Given that, a ball is dropped from a height of 10 m.
∴ Total distance travelled by the ball is = 10 + 2[6 + 3.6 + …]
The terms 6, 3.6 … are in G.P.
a = 6, r = 0.6, |r| = |0.6| < 1
∴ Sum to infinity exists.
∴ Total distance travelled by the ball