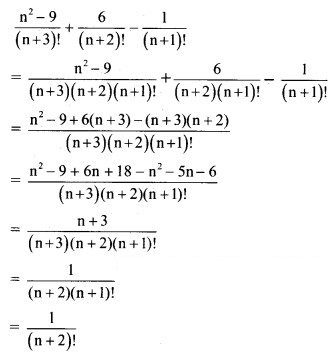Question 1.
Evaluate:
(i) 8!
Solution:
8!
= 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 40320
(ii) 10!
Solution:
10!
= 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 3628800
(iii) 10! – 6!
Solution:
10! – 6!
= 10 × 9 × 8 × 7 × 6! – 6!
= 6! (10 × 9 × 8 × 7 – 1)
= 6! (5040 – 1)
= 6 × 5 × 4 × 3 × 2 × 1 × 5039
= 3628080
(iv) (10 – 6)!
Solution:
(10 – 6)!
= 4!
= 4 × 3 × 2 × 1
= 24
Question 2.
Compute:
= 12 × 11 × 10 × 9 × 8 × 7
= 665280
= 2!
= 2 × 1
= 2
(iii) (3 × 2)!
Solution:
(3 × 2)!
= 6!
= 6 × 5 × 4 × 3 × 2 × 1
= 720
(iv) 3! × 2!
Solution:
3! × 2!
= 3 × 2 × 1 × 2 × 1
= 12
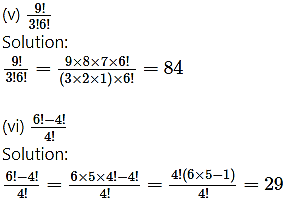
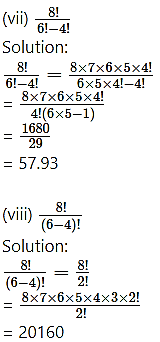
Question 3.
Write in terms of factorials
(i) 5 × 6 × 7 × 8 × 9 × 10
Solution:
5 × 6 × 7 × 8 × 9 × 10 = 10 × 9 × 8 × 7 × 6 × 5
Multiplying and dividing by 4!, we get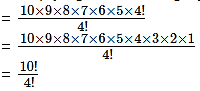
(ii) 3 × 6 × 9 × 12 × 15
Solution:
3 × 6 × 9 × 12 × 15
= 3 × (3 × 2) × (3 × 3) × (3 × 4) × (3 × 5)
= () (5 × 4 × 3 × 2 × 1)
= (5!)
(iii) 6 × 7 × 8 × 9
Solution:
6 × 7 × 8 × 9 = 9 × 8 × 7 × 6
Multiplying and dividing by 5!, we get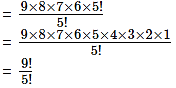
(iv) 5 × 10 × 15 × 20
Solution:
5 × 10 × 15 × 20
= (5 × 1) × (5 × 2) × (5 × 3) × (5 × 4)
= () (4 × 3 × 2 × 1)
= () (4!)
Question 4.
(i) n = 8, r = 6
(ii) n = 12, r = 12
(iii) n = 15, r = 10
(iv) n = 15, r = 8
Solution: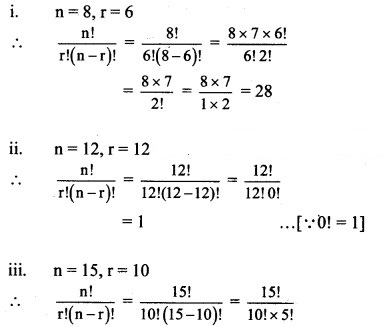

Question 5.
Find n, if
Solution:
Solution: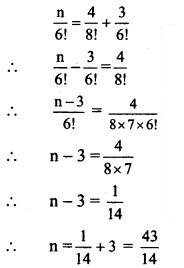
Solution:
(iv) (n + 1)! = 42 × (n -1)!
Solution:
(n + 1)! = 42(n – 1)!
∴ (n + 1) n (n – 1)! = 42(n – 1)!
∴ + n = 42
∴ + n – 42 = 0
∴ (n + 7)(n – 6) = 0
∴ n = -7 or n = 6
But n ≠ -7 as n ∈ N
∴ n = 6
(v) (n + 3)! = 110 × (n + 1)!
Solution:
(n + 3)! = (110) (n + 1)!
∴ (n + 3)(n + 2)(n + 1)! = 110(n + 1)!
∴ (n + 3) (n + 2) = (11) (10)
Comparing on both sides, we get
n + 3 = 11
∴ n = 8
Question 6.
Find n, if:
Solution: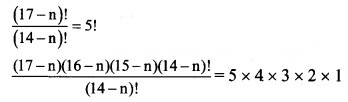
∴ (17 – n) (16 – n) (15 – n) = 6 × 5 × 4
Comparing on both sides, we get
17 – n = 6
∴ n = 11
Solution: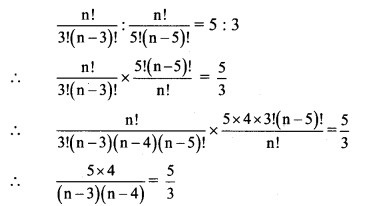
∴ 12 = (n – 3)(n – 4)
(n – 3)(n – 4) = 4 × 3
Comparing on both sides, we get
n – 3 = 4
∴ n = 7
Solution: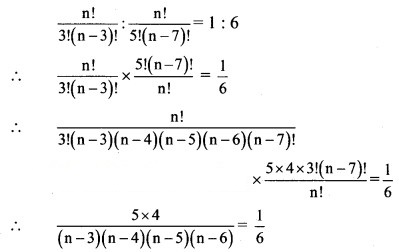
∴ 120 = (n – 3)(n – 4) (n – 5)(n – 6)
∴ (n – 3)(n – 4) (n – 5)(n – 6) = 5 × 4 × 3 × 2
Comparing on both sides, we get
n – 3 = 5
∴ n = 8
Solution: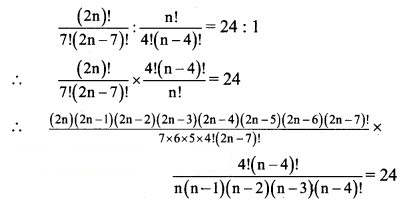
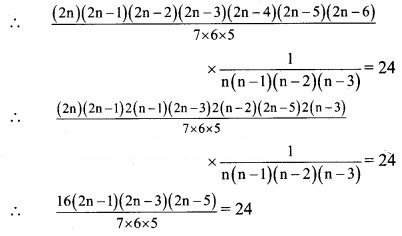
![]()
∴ (2n – 1)(2n – 3)(2n – 5) = 9 × 7 × 5
Comparing on both sides. We get
∴ 2n – 1 = 9
∴ n = 5
Question 7.
Solution:
Question 8.
Solution:
Question 9.
Solution: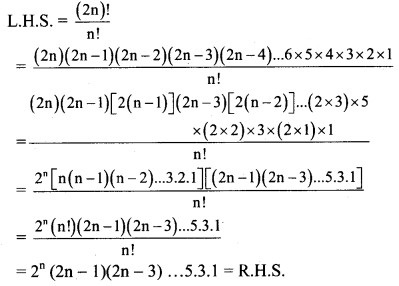
Question 10.
Simplify
Solution: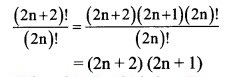
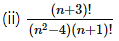
Solution: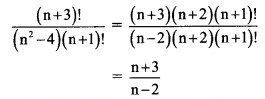
Solution: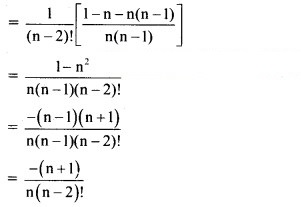
(iv) n[n! + (n – 1)!] + (n – 1)! + (n + 1)!
Solution:
Solution:
Solution: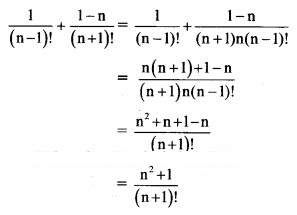
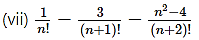
Solution: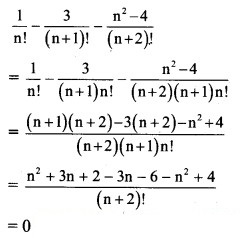
Solution: