Maharashtra Board Class 11 Maths Part 2 Chapter 4 Methods of Induction and Binomial Theorem Ex 4.1 Solution

Prove by the method of induction, for all n ∈ N.

Question 1.
2 + 4 + 6 + …… + 2n = n(n + 1)
Solution:
Let P(n) = 2 + 4 + 6 + …… + 2n = n(n + 1), for all n ∈ N.
Step I:
Put n = 1
L.H.S. = 2
R.H.S. = 1(1 + 1) = 2
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 2 + 4 + 6 + ….. + 2k = k(k + 1) ……(i)

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
2 + 4 + 6 + …… + 2(k + 1) = (k + 1) (k + 2)
L.H.S. = 2 + 4 + 6 + …+ 2(k + 1)
= 2 + 4 + 6+ ….. + 2k + 2(k + 1)
= k(k + 1) + 2(k + 1) …..[From (i)]
= (k + 1).(k + 2)
= R.H.S.
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 2 + 4 + 6 + …… + 2n = n(n + 1) for all n ∈ N.

Question 2.
3 + 7 + 11 + ……… to n terms = n(2n + 1)
Solution:
Let P(n) = 3 + 7 + 11 + ……… to n terms = n(2n +1), for all n ∈ N.
But 3, 7, 11, …. are in A.P.
∴ a = 3 and d = 4
Let t_n be the nth term.
∴ t_n = a + (n – 1)d = 3 + (n – 1)4 = 4n – 1
∴ P(n) = 3 + 7 + 11 + ……. + (4n – 1) = n(2n + 1)

Step I:
Put n = 1
L.H.S. = 3
R.H.S. = 1[2(1)+ 1] = 3
∴ L.H.S. = R.H.S.
∴ P(n) is true for n = 1.

Step II:
Let us assume that P(n) is true for n = k.
∴ 3 + 7 + 11 + ….. + (4k – 1) = k(2k + 1) …..(i)

Sept III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that
3 + 7 + 11 + …+ [4(k + 1) – 1] = (k + 1)(2k + 3)
L.H.S. = 3 + 7 + 11 + …… + [4(k + 1) – 1]
= 3 + 7 + 11 + ….. + (4k – 1) + [4(k+ 1) – 1]
= k(2k + 1) + (4k + 4 – 1) …..[From (i)]
= 2k² + k + 4k + 3
= 2k² + 2k + 3k + 3
= 2k(k + 1) + 3(k + 1)
= (k + 1) (2k + 3)
= R.H.S.
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 3 + 7 + 11 + ….. to n terms = n(2n + 1) for all n ∈ N.

Question 3.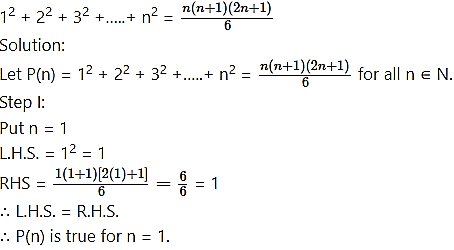

Step II:
Let us assume that P(n) is true for n = k.

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.

Question 4.

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.

Step II:
Let us assume that P(n) is true for n = k.

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.

Question 6.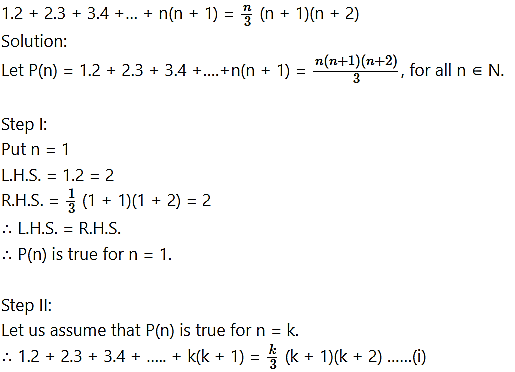

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:

Step I:

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that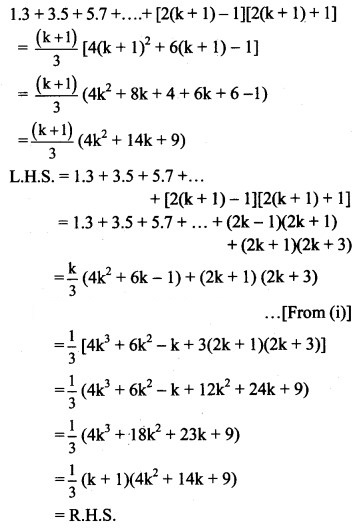

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ 1.3 + 3.5 + 5.7 +… to n terms =  (4n² + 6n – 1) for all n ∈ N.

Question 8.

Step II:
Let us assume that P(n) is true for n = k.

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.

Step I:

Step II:
Let us assume that P(n) is true for n = k.

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that


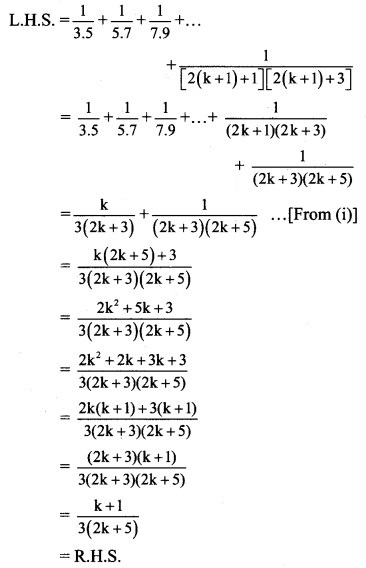
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.

Question 10.

Step III: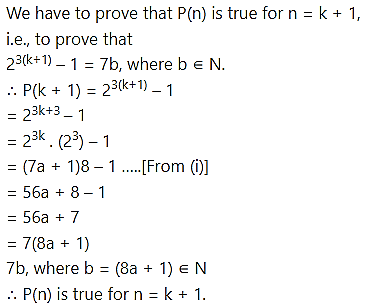

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ (2⁴ⁿ – 1) is divisible by 7, for all n ∈ N.

Question 11.

Step III:

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ (2⁴ⁿ – 1) is divisible by 15, for all n ∈ N.

Question 12.

Step III:
We have to prove that P(n) is tme for n = k + 1,
i.e., to prove that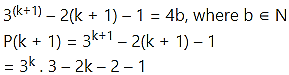

= (4a + 2k + 1) . 3 – 2k – 3 …….[From (i)]
= 12a + 6k + 3 – 2k – 3
= 12a + 4k
= 4(3a + k)
= 4b, where b = (3a + k) ∈ N
∴ P(n) is tme for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is tme for all n ∈ N.
∴ 3ⁿ – 2n – 1 is divisible by 4, for all n ∈ N.

Question 13.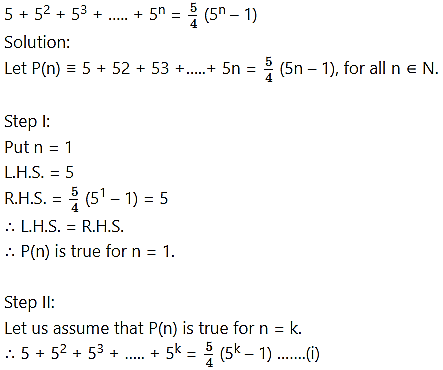

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.

Question 14.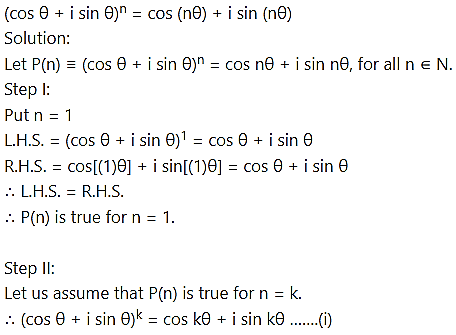

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that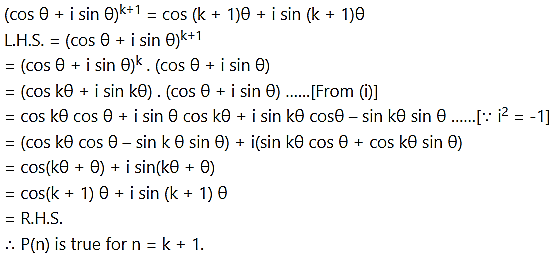

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ (cos θ + i sin θ)² = cos (nθ) + i sin (nθ), for all n ∈ N.

Question 15.

Step III:
We have to prove that P(n) is true for n = k + 1,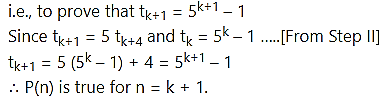

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.
∴ t_n =5ⁿ – 1, for all n ∈ N.

Question 16.
Prove by method of induction

Solution: