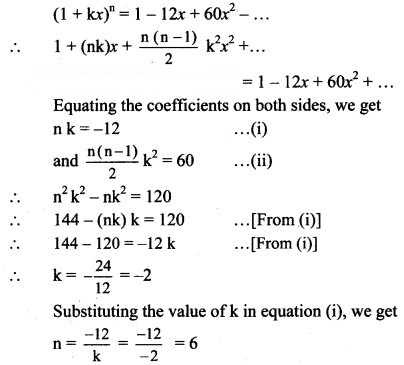Maharashtra Board Class 11 Maths Part 2 Chapter 4 Methods of Induction and Binomial Theorem Miscellaneous Exercise 4 Solution

(I) Select the correct answers from the given alternatives.

Question 1.
The total number of terms in the expression of (x + y)¹⁰⁰ + (x – y)¹⁰⁰ after simplification is:
(A) 50
(B) 51
(C) 100
(D) 202
Answer:
(B) 51
Hint: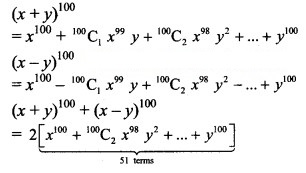

Question 2.

Question 3.

Question 4.

Hint:

Question 5.
The number of terms in expansion of (4y + x)⁸ – (4y – x)⁸ is
(A) 4
(B) 5
(C) 8
(D) 9
Answer:
(A) 4
Hint: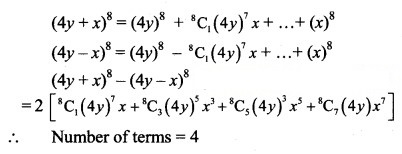

Question 6.

Hint: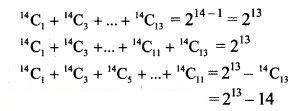

Question 7.

Hint:

Question 8.
In the expansion of (3x + 2)⁴, the coefficient of the middle term is
(A) 36
(B) 54
(C) 81
(D) 216
Answer:
(D) 216
Hint:
(3x + 2)⁴ has 5 terms.
∴ (3x + 2)⁴ has 3rd term as the middle term.
The coefficient of the middle term

= 6 × 9 × 4
= 216

Question 9.

Question 10.
If the coefficients of x² and x³ in the expansion of (3 + ax)⁹ are the same, then the value of a is

Hint:

(II) Answer the following.

Question 1.

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., 8 + 17 + 26 + …… + [9(k + 1) – 1]

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that

∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.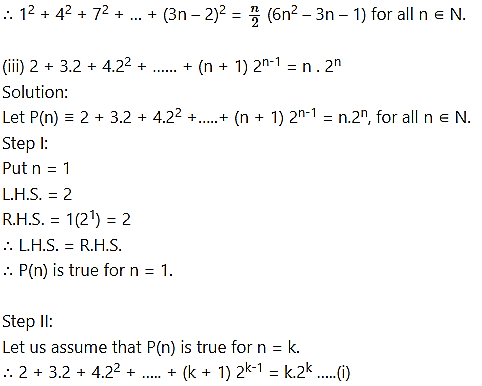

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that


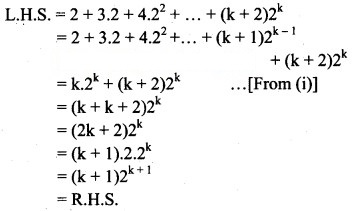
∴ P(n) is true for n = k + 1.

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.

Solution:

Question 2.

Step III:
We have to prove that P(n) is true for n = k + 1,
i.e., to prove that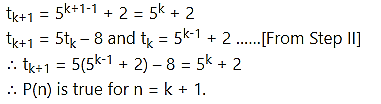

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.

Question 3.
Prove by method of induction

Solution:

Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.

Using binomial theorem,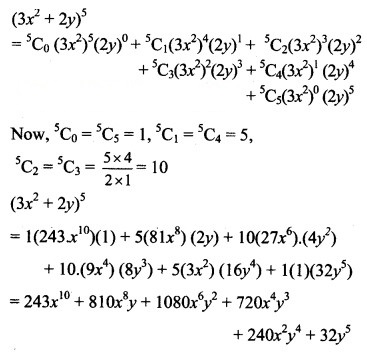

Question 5.

Solution:

Question 6.

Solution: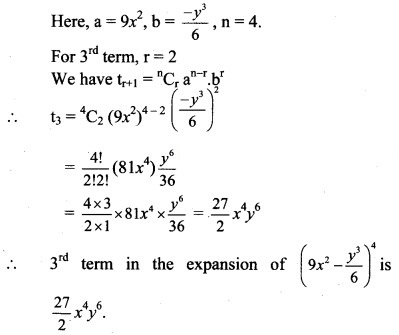

Question 7.

Solution: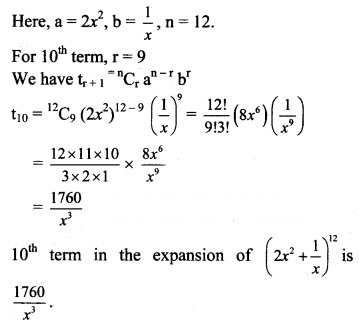

Question 8.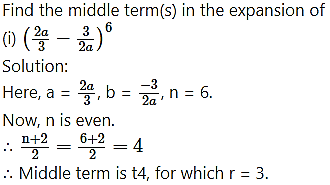


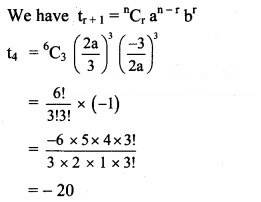
∴ The Middle term is -20.

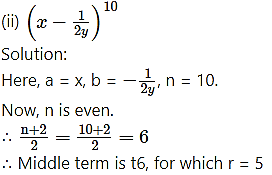
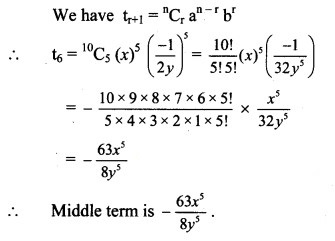
Solution: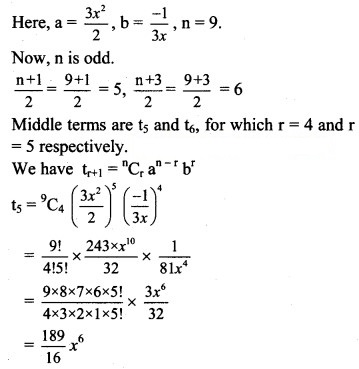

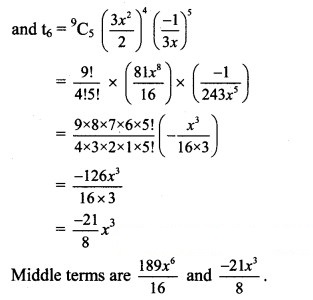
Question 9.

Solution: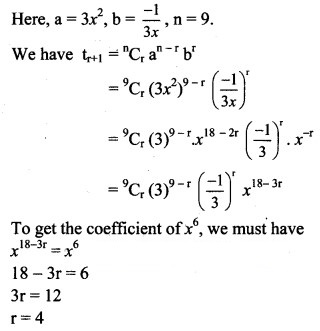

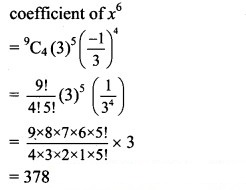
Solution:

Question 10.
Find the constant term in the expansion of

Solution:

Solution: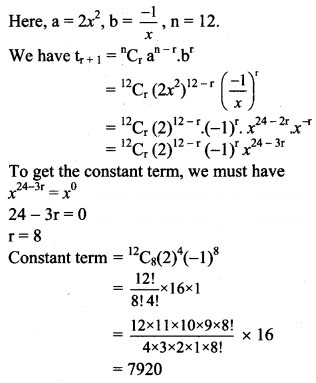

Question 11.
Prove by method of induction

Solution:

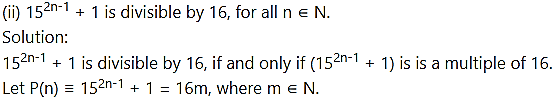
Step IV:
From all the steps above, by the principle of mathematical induction, P(n) is true for all n ∈ N.

Solution:

Question 12.
If the coefficient of x¹⁶ in the expansion of (x² + ax)¹⁰ is 3360, find a.
Solution:

Question 13.

Solution: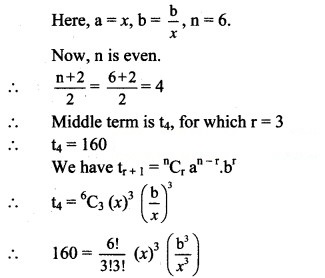

Question 14.
If the coefficients of x² and x³ in theexpansion of (3 + kx)⁹ are equal, find k.
Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.

Solution:

Question 18.

Solution: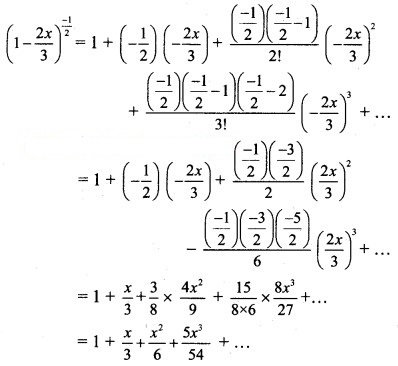

Question 19.

Solution:

Question 20.

Solution: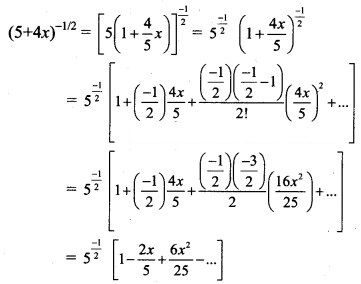

Question 21.

Solution:

Question 22.

Solution: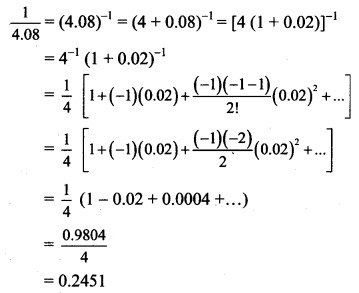

Question 23.

Solution:

Question 24.
(a + bx) (1 – x)⁶ = 3 – 20x + cx² + …, then find a, b, c.
Solution: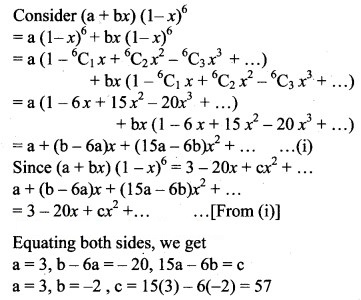

Question 25.
The 3rd term of (1 + x)ⁿ is 36x². Find 5th term.
Solution: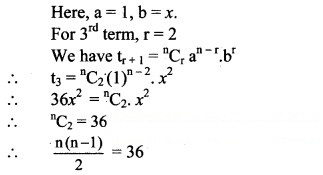

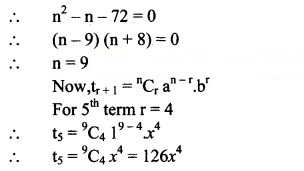
Question 26.
Suppose (1 + kx)ⁿ = 1 – 12x + 60x² – …… find k and n.
Solution: