Question 1.
If f(x) = 3x + 5, g(x) = 6x – 1, then find
(i) (f + g) (x)
(ii) (f – g) (2)
(iii) (fg) (3)
(iv) (f/g) (x) and its domain
Solution:
f(x) = 3x + 5, g (x) = 6x – 1
(i) (f + g) (x) = f (x) + g (x)
= 3x + 5 + 6x – 1
= 9x + 4
(ii) (f – g) (2) = f(2) – g(2)
= [3(2) + 5] – [6(2) – 1]
= 6 + 5 – 12 + 1
= 0
(iii) (fg) (3) = f (3) g(3)
= [3(3) + 5] [6(3) – 1]
= (14) (17)
= 238

Question 2.
Let f: (2, 4, 5} → {2, 3, 6} and g: {2, 3, 6} → {2, 4} be given by f = {(2, 3), (4, 6), (5, 2)} and g = {(2, 4), (3, 4), (6, 2)}. Write down gof.
Solution:
f = {(2, 3), (4, 6), (5, 2)}
∴ f(2) = 3, f(4) = 6, f(5) = 2
g ={(2, 4), (3, 4), (6, 2)}
∴ g(2) = 4, g(3) = 4, g(6) = 2
gof: {2, 4, 5} → {2, 4}
(gof) (2) = g(f(2)) = g(3) = 4
(gof) (4) = g(f(4)) = g(6) = 2
(gof) (5) = g(f(5)) = g(2) = 4
∴ gof = {(2, 4), (4, 2), (5, 4)}
Question 3.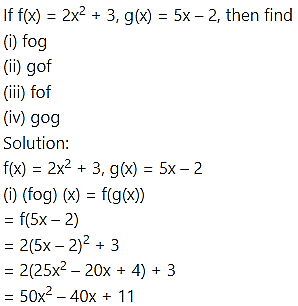
(ii) (gof) (x) = g(f(x))
= g(2x2 + 3)
= 5(2x + 3) – 2
= 10x2 + 13
(iii) (fof) (x) = f(f(x))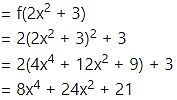
(iv) (gog) (x) = g(g(x))
= g(5x – 2)
= 5(5x – 2) – 2
= 25x – 12
Question 4.
Verify that f and g are inverse functions of each other, where

![]()
Replacing x by g(x), we get
Here, f[g(x)] = x and g[f(x)] = x.
∴ f and g are inverse functions of each other.
Question 5.
Check if the following functions have an inverse function. If yes, find the inverse function.
(vi) f(x) =
Solution:
(i) f(x) = 5x2 = y (say)
For two values (x1 and x2) of x, values of the function are equal.
∴ f is not one-one.
∴ f does not have an inverse.
(ii) f(x) = 8 = y (say)
For every value of x, the value of the function f is the same.
∴ f is not one-one i.e. (many-one) function.
∴ f does not have the inverse.
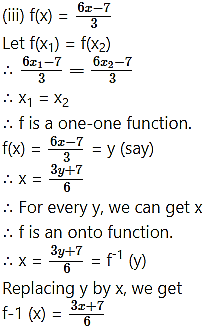
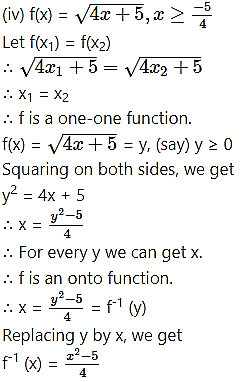
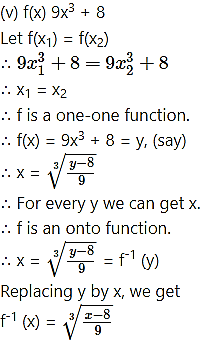
(vi) f(x) = x + 7, x < 0
= 8 – x, x ≥ 0
We observe from the graph that for two values of x, say x1 , x2 the values of the function are equal.
i.e. f(x1) = f(x2)
∴ f is not one-one (i.e. many-one) function.
∴ f does not have inverse.
Question 6.
If f(x) = , then find
(i) f(3)
(ii) f(2)
(iii) f(0)
Solution:
f(x) = x2 + 3, x ≤ 2
= 5x + 7, x > 2
(i) f(3) = 5(3) + 7
= 15 + 7
= 22
(ii) f(2) = 22 + 3
= 4 + 3
= 7
(iii) f(0) = 02 + 3 = 3
Question 7.
If f(x) = , then find
(i) f(-4)
(ii) f(-3)
(iii) f(1)
(iv) f(5)
Solution:
f(x) = 4x – 2, x ≤ -3
= 5, -3 < x < 3
= x2, x ≥ 3
(i) f(-4) = 4(-4) – 2
= -16 – 2
= -18
(ii) f(-3) = 4(-3) – 2
= -12 – 2
= -14
(iii) f(1) = 5
(iv) f(5) = 52 = 25
Question 8.
If f(x) = 2 |x| + 3x, then find
(i) f(2)
(ii) f(-5)
Solution:
f(x) = 2 |x| + 3x
(i) f(2) = 2|2| + 3(2)
= 2 (2) + 6 ….. [∵ |x| = x, x > 0]
= 10
(ii) f(-5) = 2 |-5| + 3(-5)
= 2(5) – 15 …..[∵ |x| = -x, x < 0]
= 10 – 15
= -5
Question 9.
If f(x) = 4[x] – 3, where [x] is greatest integer function of x, then find
(i) f(7.2)
(ii) f(0.5)
(iv) f(2π), where π = 3.14
Solution:
f(x) = 4[x] – 3
(i) f(7.2) = 4 [7.2] – 3
= 4(7) – 3 ………[∵ 7 ≤ 7.2 < 8, [7.2] = 7]
= 25
(ii) f(0.5) = 4[0.5] – 3
= 4(0) – 3 ………[∵ 0 ≤ 0.5 < 1, [0.5] = 0]
= -3
![]()
= 4[-2.5] – 3
= 4(-3) – 3 …….[∵-3 ≤ -2.5 ≤ -2, [-2.5] = -3]
= -15
(iv) f(2π) = 4[2π] – 3
= 4[6.28] – 3 …..[∵ π = 3.14]
= 4(6) – 3 …….[∵ 6 ≤ 6.28 < 7, [6.28] = 6]
= 21
Question 10.
If f(x) = 2{x} + 5x, where {x} is fractional part function of x, then find
(i) f(-1)
(ii) f(1/4)
(iii) f(-1.2)
(iv) f(-6)
Solution:
f(x) = 2{x} + 5x
(i) {-1} = -1 – [-1] = -1 + 1 = 0
∴ f(-1) = 2 {-1} + 5(-1)
= 2(0) – 5
= -5

(iii) {-1.2} = -1.2 – [-1.2] = -1.2 + 2 = 0.8
f(-1.2) = 2{-1.2} + 5(-1.2)
= 2(0.8) + (-6)
= -4.4
(iv) {-6} = -6 – [-6] = -6 + 6 = 0
f(-6) = 2{-6} + 5(-6)
= 2(0) – 30
= -30
Question 11.
Solve the following for x, where |x| is modulus function, [x] is the greatest integer function, {x} is a fractional part function.
(i) |x + 4| ≥ 5
(ii) |x – 4| + |x – 2| = 3
(iii) x2 + 7|x| + 12 = 0
(iv) |x| ≤ 3
(v) 2|x| = 5
(vi) [x + [x + [x]]] = 9
(vii) {x} > 4
(viii) {x} = o
(ix) {x} = 0.5
(x) 2{x} = x + [x]
Solution:
(i) |x + 4| ≥ 5
The solution of |x| ≥ a is x ≤ -a or x ≥ a
∴ |x + 4| ≥ 5 gives
∴ x + 4 ≤ -5 or x + 4 ≥ 5
∴ x ≤ -5 – 4 or x ≥ 5 – 4
∴ x ≤ -9 or x ≥ 1
∴ The solution set = (-∞, – 9] ∪ [1, ∞)
(ii) |x – 4| + |x – 2| = 3 …..(i)
Case I: x < 2
Equation (i) reduces to
4 – x + 2 – x = 3 …….[x < 2 < 4, x – 4 < 0, x – 2 < 0]
∴ 6 – 3 = 2x
∴ x = 3/2
Case II: 2 ≤ x < 4
Equation (i) reduces to
4 – x + x – 2 = 3
∴ 2 = 3 (absurd)
There is no solution in [2, 4)
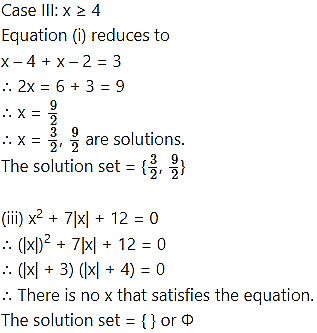
(iv) |x| ≤ 3 The solution set of |x| ≤ a is -a ≤ x ≤ a
∴ The required solution is -3 ≤ x ≤ 3
∴ The solution set is [-3, 3]
(v) 2|x| = 5
∴ |x| = 5/2
∴ x = ±5/2
(vi) [x + [x + [x]]] = 9
∴ [x + [x] + [x] ] = 9 …….[[x + n] = [x] + n, if n is an integer]
∴ [x + 2[x]] = 9
∴ [x] + 2[x] = 9 …..[[2[x] is an integer]]
∴ [x] = 3
∴ x ∈ [3, 4)
(vii) {x} > 4
This is a meaningless statement as 0 ≤ {x} < 1
∴ The solution set = { } or Φ
(viii) {x} = 0
∴ x is an integer
∴ The solution set is Z.
(ix) {x} = 0.5
∴ x = ….., -2.5, -1.5, -0.5, 0.5, 1.5, …..
∴ The solution set = {x : x = n + 0.5, n ∈ Z}
(x) 2{x} = x + [x]
= [x] + {x} + [x] ……[x = [x] + {x}]
∴ {x} = 2[x]
R.H.S. is an integer
∴ L.H.S. is an integer
∴ {x} = 0
∴ [x] = 0
∴ x = 0
