Maharashtra Board Class 11 Physics Chapter 2 Mathematical Methods Solution

Chapter 2 Mathematical Methods

1. Choose the correct option.

Question 1.
The resultant of two forces 10 N and 15 N acting along + x and – x-axes respectively, is
(A) 25 N along + x-axis
(B) 25 N along – x-axis
(C) 5 N along + x-axis
(D) 5 N along – x-axis
Answer:
(D) 5 N along – x-axis

Question 2.
For two vectors to be equal, they should have the
(A) same magnitude
(B) same direction
(C) same magnitude and direction
(D) same magnitude but opposite direction
Answer:
(C) same magnitude and direction

Question 3.
The magnitude of scalar product of two unit vectors perpendicular to each other is
(A) zero
(B) 1
(C) -1
(D) 2
Answer:
(A) zero

Question 4.
The magnitude of vector product of two unit vectors making an angle of 60° with each other is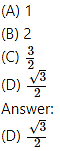

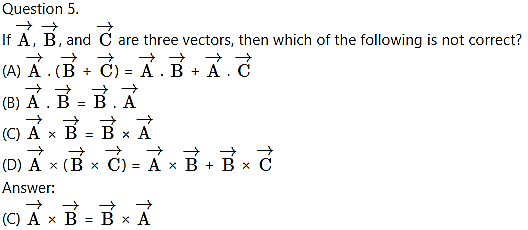
2. Answer the following questions.

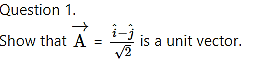
Solution:

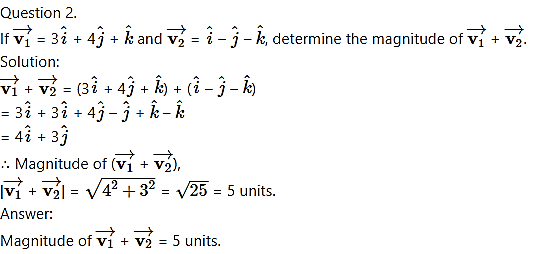
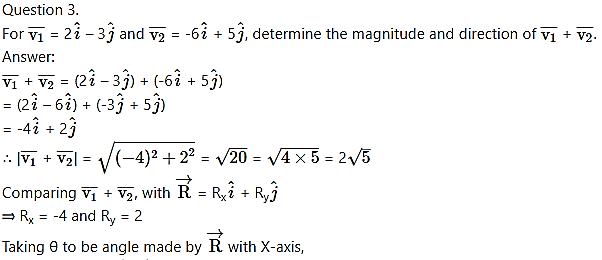
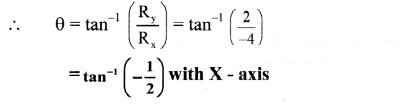
Answer: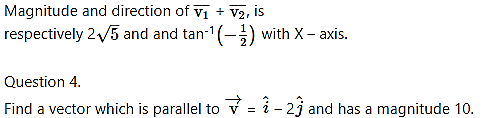

Answer:

Substituting for w_x in (i) using equation (ii),

Using equation (ii),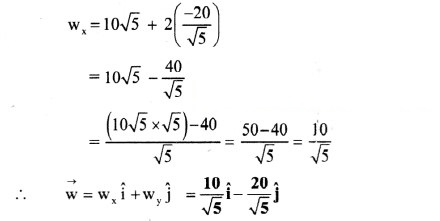

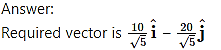
Alternate method:

When two vectors are parallel, one vector is scalar multiple of another,

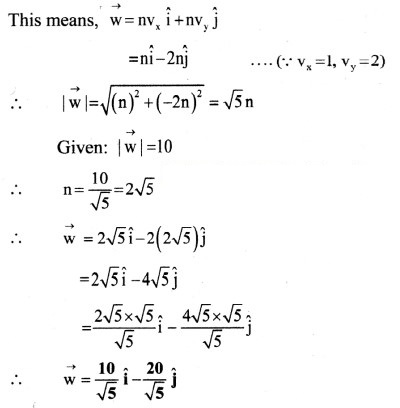
Answer:
Let angle between two vectors be θ.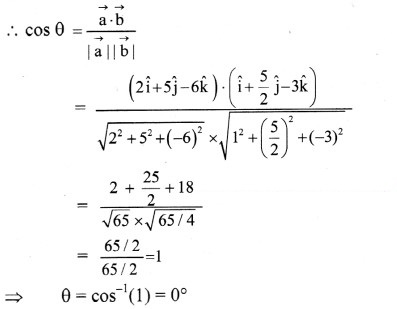

⇒ Two vectors are parallel.

Alternate method:

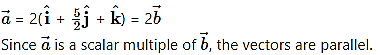
3. Solve the following problems.

Answer:
Using determinant for vectors in two dimensions,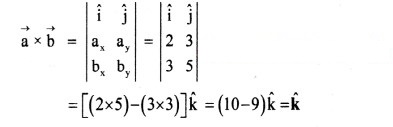


Solution:
As dot product of two perpendicular vectors is zero. Taking dot product of a⃗  and b⃗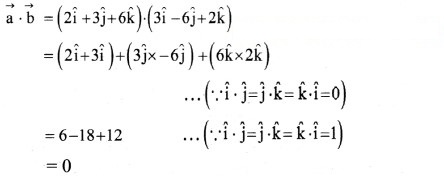 

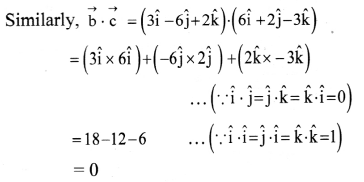
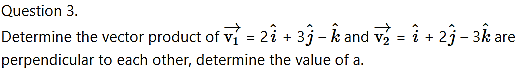
Solution:



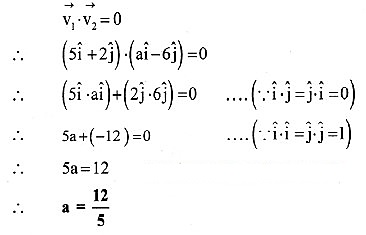
Answer:
Value of a is .

Question 5.
Obtain derivatives of the following functions:
(i) x sin x
(ii) x⁴ + cos x
(iii) x/sin x
Answer:
(i) x sin x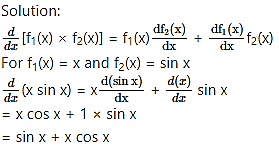

(ii) x⁴ + cos x
Solution: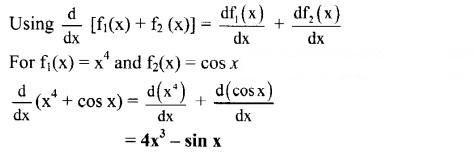

(iii) 
Solution: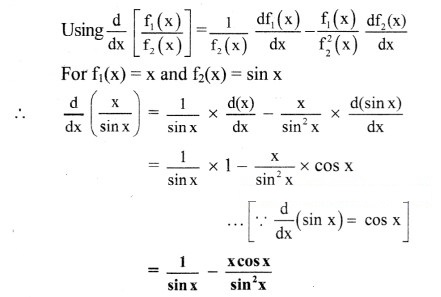

[Note: As derivative of (sin x) is cos x, negative sign that occurs in rule for differentiation for quotient of two functions gets retained in final answer]

Question 6.
Using the rule for differentiation for quotient of two functions, prove that  = sec²x
Solution: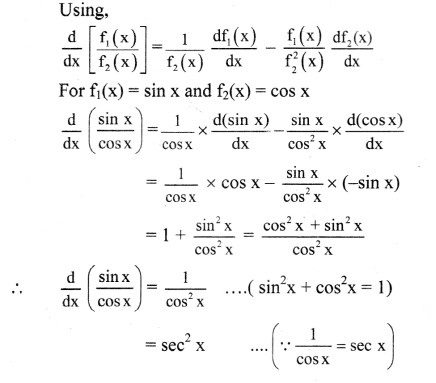

Question 7.
Evaluate the following integral:
(i) ∫π/20sinxdx
(ii) ∫51xdx
Answer:
(i) ∫π/20sinxdx
Solution: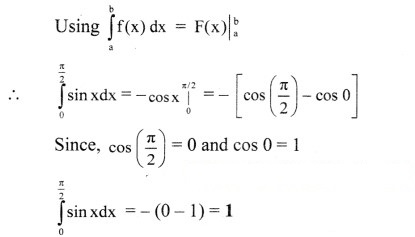

(ii) ∫51xdx
Solution: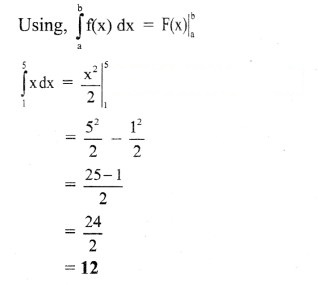

Intext Questions and Answers

Can you recall? (Textbook Page No. 16)

Question 1.
Define scalars and vectors.
Answer:

1. Physical quantities which can be completely described b their magnitude (a number and unit) are called scalars.
2. Physical quantities which need magnitude, as well as direction for their complete description, are called vectors.

Question 2.
Which of the following are scalars or vectors?
Displacements, distance travelled, velocity, speed, force, work done, energy
Answer:

1. Scalars: Distance travelled, speed, work done, energy.
2. Vectors: Displacement, velocity, force.

Question 3.
What is the difference between a scalar and a vector?
Answer:

No.	Scalars	Vectors
i.	It has magnitude only	It has magnitude as well as direction.
ii.	Scalars can be added or subtracted according to the rules of the algebra.	Vectors are added or subtracted by the geometrical (graphical) method or vector algebra.
iii.	It has no specific representation.	It is represented by the symbol (→) arrow.
iv.	The division of a scalar by another scalar is valid.	The division of a vector by another vector is not valid.
	Example: Length, mass, time, volume, etc.	Example: Displacement, velocity, acceleration, force, etc.

Internet my friend (Textbook page no. 28)

1. hyperphysics.phy-astr.gsu.edu/hbase/vect. html#veccon
2. hyperphysics.phy-astr.gsu.edu/hbase/ hframe.html

Answer:
[Students can use links given above as a reference and collect information about mathematical methods]