Maharashtra Board Class 12 Physics Solutions Chapter 10 Magnetic Fields due to Electric Current

Chapter 10 Magnetic Fields due to Electric Current

1. Choose the correct option.

i) A conductor has 3 segments; two straight and of length L each and a semicircular with radius R. It carries a current I. What is the magnetic field B at point P?

Answer:

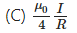
Answer:
(A) -μ₀ I, 0

iii) A proton enters a perpendicular uniform magnetic field B at origin along the positive x axis with a velocity v as shown in the figure. Then it will follow the following path. [The magnetic field is directed into the paper].

(A) It will continue to move along positive x axis.
(B) It will move along a curved path, bending towards positive x axis.
(C) It will move along a curved path, bending towards negative y axis.
(D) It will move along a sinusoidal path along the positive x axis.
Answer:
(C) It will move along a curved path, bending towards negative y axis.

(iv) A conducting thick copper rod of length 1 m carries a current of 15 A and is located on the Earth’s equator. There the magnetic flux lines of the Earth’s magnetic field are horizontal, with the field of 1.3 × 10^-4 T, south to north. The magnitude and direction of the force on the rod, when it is oriented so that current flows from west to east, are
(A) 14 × 10^-4 N, downward.
(B) 20 × 10^-4 N, downward.
(C) 14 × 10^-4 N, upward.
(D) 20 × 10^-4 N, upward.
Answer:
(D) 20 × 10^-4 N, upward.

(A) remain uncharged.
(B) get reduced.
(C) increase.
(D) be reduced to zero.
Answer:
(A) remain uncharged.

Question 2.
A piece of straight wire has mass 20 g and length 1m. It is to be levitated using a current of 1 A flowing through it and a perpendicular magnetic field B in a horizontal direction. What must be the magnetic of B?

Answer:
Data: m = 20 g = 2 × 10^-2 kg, l = 1 m, I = 1 A,
g = 9.8 m/s²
To balance the wire, the upward magnetic force must be equal in magnitude to the downward force due to gravity.
∴ F_m = IlB = mg
Therefore, the magnitude of the magnetic field,

Question 3.
Calculate the value of magnetic field at a distance of 2 cm from a very long straight wire carrying a current of 5 A (Given: µ₀ = 4π × 10^-7 Wb/Am).
Answer:

Question 4.
An electron is moving with a speed of 3.2 × 10⁶ m/s in a magnetic field of 6.00 × 10^-4 T perpendicular to its path. What will be the radius of the path? What will be frequency and the kinetic energy in keV ? [Given: mass of electron = 9.1 × 10^-31 kg, charge e = 1.6 × 10^-19 C, 1 eV = 1.6 × 10^-19 J]
Answer:

Question 5.
An alpha particle (the nucleus of helium atom) (with charge +2e) is accelerated and moves in a vacuum tube with kinetic energy = 10.00 MeV.On applying a transverse a uniform magnetic field of 1.851 T, it follows a circular trajectory of radius 24.60 cm. Obtain the mass of the alpha particle. [charge of electron = 1.62 × 10^-19 C]
Answer:
Data: 1 eV = 1.6 × 10^-19 J,
E = 10MeV = 10⁷ × 1.6 × 10^-19 J = 1.6 × 10^-12 J
B = 1.88 T, r = 0.242 m, e = 1.6 × 10^-19 C
Charge of an -partic1e,
q = 2e = 2(1.6 × 10^-19)=3.2 × 10^-19 C

This gives the mass of the α-particle.
[Note : The value of r has been adjusted to match with the answer. The CODATA (Committee on Data for Science and Technology) accepted value of m_x is approximately 6.6446 × 10^-27 kg.]

Question 6.
Two wires shown in the figure are connected in a series circuit and the same amount of current of 10 A passes through both, but in apposite directions. Separation between the two wires is 8 mm. The length AB is S = 22 cm. Obtain the direction and magnitude of the magnetic field due to current in wire 2 on the section AB of wire 1. Also obtain the magnitude and direction of the force on wire 1. [µ₀ = 4π × 10^-7 T.m/A]

Answer:

Question 7.
A very long straight wire carries a current 5.2 A. What is the magnitude of the magnetic field at a distance 3.1 cm from the wire? [ µ₀ = 4π × 10^-7 T∙m/A]
Answer: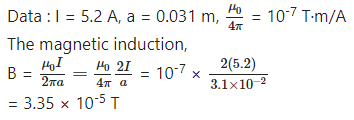

Question 8.
Current of equal magnitude flows through two long parallel wires having separation of 1.35 cm. If the force per unit length on each of the wires in 4.76 × 10^-2 N, what must be I ?
Answer:

Question 9.
Magnetic field at a distance 2.4 cm from a long straight wire is 16 µT. What must be current through the wire?
Answer:

Question 10.
The magnetic field at the centre of a circular current carrying loop of radius 12.3 cm is 6.4 × 10^-6T. What will be the magnetic moment of the loop?
Answer:
Data: R = 12.3cm = 12.3 × 10^-2 m,
B = 6.4 × 10^-6 T, µ₀ = 4π × 10^-7 T∙m/A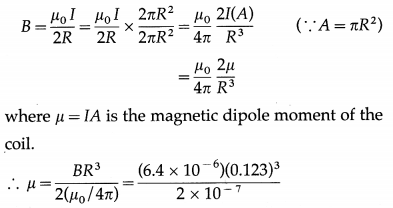

= 5.955 × 10^-2 J/T (or A∙m²)

Question 11.
A circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the magnetic field (a) at the centre of the loop and (b) at a distance of 9.7 cm from the centre of the loop but on the axis.
Answer:
Data: R = z = 9.7 cm = 9.7 × 10^-2 m, I = 2.3A, N = 1
(a) At the centre of the coil :
The magnitude of the magnetic induction,

Question 12.
A circular coil of wire is made up of 100 turns, each of radius 8.0 cm. If a current of 0.40 A passes through it, what be the magnetic field at the centre of the coil?
Answer:

Question 13.
For proton acceleration, a cyclotron is used in which a magnetic field of 1.4 Wb/m² is applied. Find the time period for reversing the electric field between the two Ds.
Answer:

Question 14.
A moving coil galvanometer has been fitted with a rectangular coil having 50 turns and dimensions 5 cm × 3 cm. The radial magnetic field in which the coil is suspended is of 0.05 Wb/m². The torsional constant of the spring is 1.5 × 10^-9 Nm/ degree. Obtain the current required to be passed through the galvanometer so as to produce a deflection of 30°.
Answer: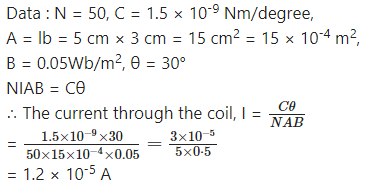

Question 15.
A solenoid of length π m and 5 cm in diameter has winding of 1000 turns and carries a current of 5 A. Calculate the magnetic field at its centre along the axis.
Answer: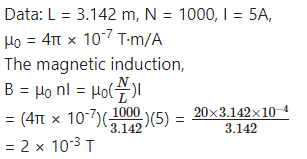

Question 16.
A toroid of narrow radius of 10 cm has 1000 turns of wire. For a magnetic field of 5 × 10^-2 T along its axis, how much current is required to be passed through the wire?
Answer:

Question 17.
In a cyclotron protons are to be accelerated. Radius of its D is 60 cm. and its oscillator frequency is 10 MHz. What will be the kinetic energy of the proton thus accelerated?
(Proton mass = 1.67 × 10^-27 kg, e = 1.60 × 10^-19 C, 1eV = 1.6 × 10^-19 J)
Answer:
Data : R = 0.6 m, f = 10⁷ Hz, m_p = 1.67 × 10^-27 kg,
e = 1.6 × 10^-19C, 1 eV = 1.6 × 10^-19 J

Question 18.


Answer:



This is the required expression.

Question 19.

Answer:

Question 20.
Figure shows a section of a very long cylindrical wire of diameter a, carrying a current I. The current density which is in the direction of the central axis of the wire varies linearly with radial distance r from the axis according to the relation J = J_or/a. Obtain the magnetic field B inside the wire at a distance r from its centre.
[Answer: B J r

Answer:
Consider an annular differential element of radius r and width dr. The current through the area dA of this element is


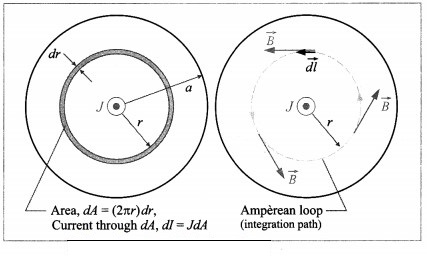
To apply the Ampere’s circuital law to the circular path of integration, we note that the wire has perfect cylindrical symmetry with all the charges moving parallel to the wire. So, the magnetic field must be tangent to circles that are concentric with the wire. The enclosed current is the current within radius r. Thus,

Question 21.
In the above problem, what will be the magnetic field B inside the wire at a distance r from its axis, if the current density J is uniform across the cross section of the wire?
Answer:

OR

Theory Exercise

Question 1.

Question 2.
Under what condition a charge undergoes uniform circular motion in a magnetic field? Describe, with a neat diagram, cyclotron as an application of this principle. Obtain an expression for the frequency of revolution in terms of the specific charge and magnetic field.
Answer:


If the charge moves in a circle of radius R,

where p = mv is the linear momentum of the particle. Equation (1) is known as the cyclotron formula because it describes the motion of a particle in a cyclotron-the first of the modern particle accelerators.

Question 3.
What is special about a radial magnetic field ? Why is it useful in a moving coil galvanometer ?
Answer:

1. Advantage of radial magnetic field in a moving- coil galvanometer:
   • As the coil rotates, its plane is always parallel to the field. That way, the deflecting torque is always a ximum depending only on the current in the coil, but not on the position of the coil.
   • The restoring torque is proportional to the deflection so that a radial field makes the deflection proportional to the current. The instrument then has a linear scale, i.e., the divisions of the scale are evenly spaced. This makes it particularly straight forward to calibrate and to read.
2. Producing radial magnetic field :
   • The pole pieces of the permanent magnet are made cylindrically concave, concentric with the axis of the coil.
   • A soft iron cylinder is centred between the pole pieces so that it forms a narrow cylindrical gap in which the sides of the coil can move. Together, they produce a radial magnetic, field; that is, the magnetic lines of force in the gap are along radii to the central axis.

Question 4.
State Biot-Savert law. Apply it to
(i) infinitely long current carrying conductor and (ii) a point on the axis of a current carrying circular loop.
Answer:
Consider a very short segment of length dl of a wire carrying a current I. The product I    is called a current element; the direction of the vector    is along the wire in the direction of the current.

Biot-Savart law (Laplace law) : The magnitude of the incremental magnetic induction   produced by a current element I   at a distance r from it is directly proportional to the magnitude I   of the current element, the sine of the angle between the current element Idl and the unit vector r directed from the current element toward the point in question, and inversely proportional to the square of the distance of the point from the current element; the magnetic induction is directed perpendicular to both I    and  as per the cross product rule.

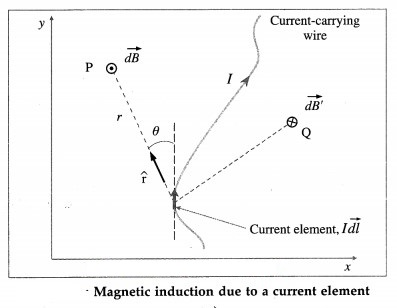
The magnetic induction    at the point due to the entire wire is, by the principle of superposition, the vector sum of the contributions   from all the current elements making up the wire.
From Eq. (2),

[Notes : (1) The above law is based on experiments by Jean Baptiste Biot (1774-1862) and Felix Savart (1791-1841), French physicists. From their observations Laplace deduced the law mathematically. (2) The Biot- Savart law plays a similar role in magnetostatics as Coulomb’s law does in electrostatics.]

Question 5.
State Ampere’s law. Explain how is it useful in different situations.
Answer:
Ampere’s circuital law : In free space, the line integral of magnetic induction around a closed path in a magnetic field is equal to p0 times the net steady current enclosed by the path.
In mathematical form,

where     is the magnetic induction at any point on the path in vacuum,  . is the length element of the path, I is the net steady current enclosed and μ₀ is the permeability of free space.

Explanation : Figure shows two wires carrying currents I₁ and I₂ in vacuum. The magnetic induction   at any point is the net effect of these currents.

To find the magnitude B of the magnetic induction :
We construct an imaginary closed curve around the conductors, called an Amperian loop, and imagine it divided into small elements of length  . The direction of dl is the direction along which the loop is traced.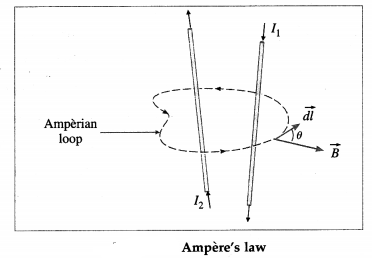

(ii) We assign signs to the currents using the right hand rule : If the fingers of the right hand are curled in the direction in which the loop is traced, then a current in the direction of the outstretched thumb is taken to be positive while a current in the opposite direction is taken to be negative.

For the case shown in Fig., the net current I through the surface bounded by the loop is
I = I₂ – I₁
∴ ∮Bcosθdl = μ₀ I
= μ₀(I₂ – I₁) …………… (3)
Equation (3) can be solved only when B is uniform and hence can be taken out of the integral.

[Note : Ampere’s law in magnetostatics plays the part of Gauss’s law of electrostatics. In particular, for currents with appropriate symmetry, Ampere’s law in integral form offers an efficient way of calculating the magnetic field. Like Gauss’s law, Ampere’s law is always true (for steady currents), but it is useful only when the symmetry of the problem enables B to be taken out of the integral ∮  .  The current configurations that can be handled by Ampere’s law are infinite straight conductor, infinite plane, infinite solenoid and toroid.]

Questions and Answers

Do you know (Textbook Page No. 230)

Question 1.
You must have noticed high tension power transmission lines, the power lines on the big tall steel towers. Strong magnetic fields are created by these lines. Care has to be taken to reduce the exposure levels to less than 0.5 milligauss (mG).
Answer:
With increasing population, many houses are constructed near high voltage overhead power transmission lines, if not right below them. Large transmission lines configurations with high voltage and current levels generate electric and magnetic fields and raises concerns about their effects on humans located at ground surfaces. With conductors typically 20 m above the ground, the electric field 2 m above the ground is about 0.2 kV / m to I kV / m. In comparison, that due to thunderstorms can reach 20 kV/m. For the same conductors, magnetic field 2 m above the ground is less than 6 μT. In comparison, that due to the Earth is about 40 μT.

Do you know (Textbook Page No. 232)

Question 1.
Magnetic Resonance Imaging (MRI) technique used for medical imaging requires a magnetic field with a strength of 1.5 T and even upto 7 T. Nuclear Magnetic Resonance experiments require a magnetic field upto 14 T. Such high magnetic fields can be produced using superconducting coil electromagnet. On the other hand, Earth’s magnetic field on the surface of the Earth is about 3.6 × 10^-5 T = 0.36 gauss.
Answer:
Magnetic Resonance Imaging (MRI) is a non-invasive imaging technology that produces three dimensional detailed anatomical images. Although MRI does not emit the ionizing radiation that is found in X-ray imaging, it does employ a strong magnetic field, e.g., medical MRIs usually have strengths between 1.5 T and 3 T.

The 21.1 T superconducting magnet at Maglab (Florida, US) is the world’s strongest MRI scanner used for Nuclear Magnetic Resonance (NMR) research. Since its inception in 2004, it has been continually conducting electric current of 284 A by itself. Because it is superconducting, the current runs through some 152 km of wire without resistance, so no outside energy source is needed. However, 2400 litres of liquid helium is cycled to keep the magnet at a superconducting temperature of 1.7 K. Even when not in use this magnet is kept cold; if it warms up to room temperature, it takes at least six weeks to cool it back down to operating temperature. The 45 T Hybrid Magnet of the Lab (which combines a superconducting magnet of 11.5 T with a resistive magnet of 33.5 T) is kept at 1.8 K using 2800 L of liquid helium and 15142 L of cold water.

Question 2.
Let us look at a charged particle which is moving in a circle with a constant speed. This is uniform circular motion that you have studied earlier. Thus, there must be a net force acting on the particle, directed towards the centre of the circle. As the speed is constant, the force also must be constant, always perpendicular to the velocity of the particle at any given instant of time. Such a force is provided by the uniform magnetic field   perpendicular to the plane of the circle along which the charged particle moves.
Answer:
When a charged particle moves in uniform circular motion inside a uniform magnetic field    in a plane perpendicular to    , the centripetal force is the magnetic force on the particle. As in any UCM, this magnetic force is constant in magnitude and perpendicular to the velocity of the particle.

Remember this (Textbook Page No. 233)

Question 1.
Field penetrating into the paper is represented as ⊗, while that coming out of the paper is shown by ⊙.
Answer:
In a two-dimensional diagram, a vector pointing perpendicularly into the plane of the diagram is shown by a cross ⊗ while that pointing out of the plane is shown by a dot ⊙ .

Do you know (Textbook Page No. 234)

Question 1.
Particle accelerators are important for a variety of research purposes. Large accelerators are used in particle research. There have been several accelerators in India since 1953. The Department of Atomic Energy (DAE), Govt. of India, had taken initiative in setting up accelerators for research. Apart from ion accelerators, the DAE has developed and commissioned a 2 GeV electron accelerator which is a radiation source for research in science. This accelerator, ‘Synchrotron’, is fully functional at Raja Ramanna Centre for Advanced Technology, Indore. An electron accelerator, Microtron with electron energy 8-10 MeV is functioning at Physics Department, Savitribai Phule Pune University, Pune.
Answer:
Particle accelerators are machines that accelerate charged subatomic particles to high energy for research and applications. They play a major role in the field of basic and applied sciences, in our understanding of nature and the universe. The size and cost of particle accelerators increase with the energy of the particles they produce. Medical Cyclotrons across the country are dedicated for medical isotope productions and for medical sciences. There are many existing and upcoming particle accelerators in India in different parts of country.

(https: / / www.researchgate.net/ publication/ 3209480 83_Existing and upcoming_particle_accelerators_in. India). For cutting-edge high energy particle physics, Indian particle physicists collaborate with those at Large Hadron Collider CERN, Geneva.

Can you recall (Textbook Page No. 238)

Question 1.
How does the coil in a motor rotate by a full rotation? In a motor, we require continuous rotation of the current carrying coil. As the plane of the coil tends to become parallel to the magnetic field  , the current in the coil is reversed externally. Referring to Fig. the segment ab occupies the position cd. At this position of rotation, the current is reversed. Instead of from b to a, it flows from a to b, force m continues to act in the same direction so that the torque continues to rotate the coil. The reversal of the current is achieved by using a commutator which connects the wires of the power supply to the coil via carbon brush contacts.
Answer:
Electric Motor
From Fig. we see that the torque on a current loop rotates the loop to smaller values of 9 until the torque becomes zero, when the plane of the loop is perpendicular to the magnetic field and θ = 0. If the current in the loop remains in the same direction when the loop turns past this position, the torque will reverse direction and turn the loop in the opposite direction, i.e., anticlockwise. To provide continuous rotation in the same sense, the current in the loop must periodically reverse direction, as shown in Fig.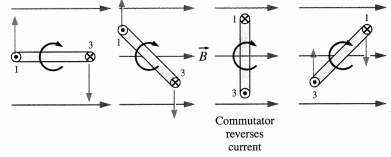

In an electric motor, the current reversal is achieved externally by brushes and a split-ring commutator.

Use your brain power (Textbook Page No. 242)

Question 1.
Currents in two infinitely long, parallel wires exert forces on each other. Is this consistent with Newton’s third law?
Answer:
Yes, they are equal in magnitude and opposite in direction and act on the

Do you know (Textbook Page No. 244)

Question 1.
So far we have used the constant µ₀ everywhere. This means in each such case, we have carried out the evaluation in free space (vacuum). µ₀ is the permeability of free space.
Answer:
Permeability of free space or vacuum, µ₀ = 4π × 10^-7 H/m.
Earlier SI (2006) had fixed this value of µ₀ as exact but revised SI fixes the value of e, requiring µ₀ (and ε₀) to be determined experimentally.

Use your brain power (Textbook Page No. 244)

Question 1.
Using electrostatic analogue, obtain the magnetic field _equator at a distance d on the perpendicular bisector of a magnetic dipole of magnetic length 2l and moment  . For far field, verify that

Answer:
The magnitude of the electric intensity at a point at a distance r from an electric charge q in vacuum is given by
E = 14πε0|q|r2
where ε₀ is the permittivity of free space. This intensity is directed away from the charge, if the charge is positive and towards the charge, if the charge is negative.

A magnetic pole is similar to an electric charge. The N-pole is similar to a positive charge and the S-pole is similar to a negative charge. Like an electric charge, a magnetic pole is assumed to produce a magnetic field in the surrounding region. The magnetic field at any point is denoted by a vector quantity called magnetic induction. Thus, by analogy, the magnitude of the magnetic induction at a point at a distance r from a magnetic pole of strength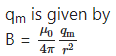 
This induction is directed away from the pole if it is an N-pole (strength + q_m) and towards the pole if it is an S-pole (strength -q_m).

Consider a point P on the equator of a magnetic dipole with pole strengths + q_m and – q_m and of magnetic length 21. Let P be at a distance d from the centre of the dipole,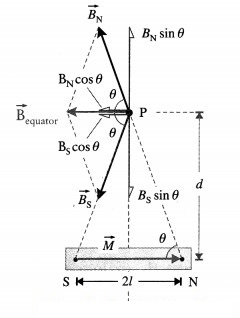

The magnetic induction of a bar magnet at an equatorial point

The magnetic induction at P due to the N-pole is directed along NP (away from the N-pole) while that due to the S-pole is along PS (towards the S-pole), each having a magnitude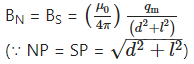

The inductions due to the two poles are equal in magnitude so that the two, oppositely directed equatorial components, B_N sin θ and B_S sin θ, cancel each other.

Therefore, the resultant induction is in a direction’ parallel to the axis of the magnetic dipole and has direction opposite to that of the magnetic moment of the magnetic dipole. The component of the induction due to the two poles along the axis is

where θ is the angle shown in the diagram. From the diagram,

Thus, for a short dipole the induction varies in-versely as the cube of the distance from it.

Question 2.
What is the fundamental difference between an electric dipole and a magnetic dipole?
Answer:
If a magnet is carefully and repeatedly cut, it would expose two new faces with opposite poles such that each piece would still be a magnet. This suggests that magnetic fields are essentially dipolar in character. The most elementary magnetic structure always behaves as a pair of two magnetic poles of opposite types and of equal strengths. Hence, analogous to an electric dipole, we hypothesize that there are positive and negative magnetic charges (or north and south poles) of equal strengths a finite distance apart within a magnet. Also, they are assumed to act as the source of the magnetic field in exactly the same way that electric charges act as the source of electric field. The magnitude of each ‘magnetic charge’ is referred to as its ‘pole strength’ and is equal to    is the magnetic dipole moment, pointing from the negative (or south, S) pole to the positive (or north, N) pole.

However, while two types of electric charges exist in nature and have separate existence, isolated magnetic charges, or magnetic monopoles, are not observed. A magnetic pole is not an experimental fact: there are no real poles. To put it in another way, there are no point sources for    , as there are for  ; there exists no magnetic analog to electric charge. Every experimental effort to demonstrate the existence of magnetic charges has failed. Hence, magnetic poles are called fictitious.

The electric field diverges away from a (positive) charge; the magnetic field line curls around a current. Electric field lines originate on positive charges and terminate on negative ones; magnetic field lines do not begin or end anywhere, they typically form closed loops or extend out to infinity.

Do you know (Textbook Page No. 247)

Question 1.
What is an ideal solenoid?
Answer:
A solenoid is a long wire wound in the form of a helix. An ideal solenoid is tightly wound and infinitely long, i.e., its turns are closely spaced and the solenoid is very long compared to its crosssectional radius.

Each turn of a solenoid acts approximately as a circular loop. Suppose the solenoid carries a steady current I. The net magnetic field due to the current in the solenoid is the vector sum of the fields due to the current in all the turns. In the case of a tightly- wound solenoid of finite length, Fig. 10.39, the magnetic field lines are approximately parallel only near the centre of the solenoid, indicating a nearly uniform field there. However, close to the ends, the field lines diverge from one end and converge at the other end. This field distribution is similar to that of a bar magnet. Thus, one end of the solenoid behaves like the north pole of a magnet and the opposite end behaves like the south pole. The field outside is very weak near the midpoint.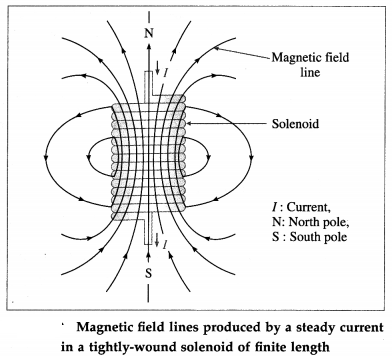

For an ideal solenoid, the magnetic field inside is reasonably uniform over the cross section and parallel to the axis throughout the volume enclosed by the solenoid. The field outside is negligible in this case.

Use your brain power (Textbook Page No. 248)

Question 1.
Choosing different Amperean loops, show that out-side an ideal toroid B = 0.
Answer:
From below figure, the inner Amperean loop does not enclose any current while the outer Amperean loop encloses equal number of I_in and I_out. Hence, by Ampere’s law, B = 0 outside an ideal toroid.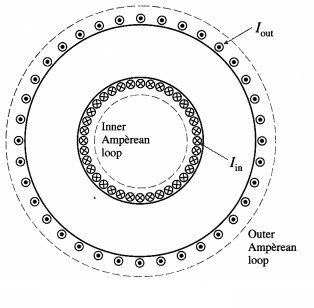

Question 2.
What is an ideal toroid?
Answer:
A toroid is a toroidal solenoid. An ideal toroid consists of a long conducting wire wound tightly around a torus, a doughnut-shaped ring, made of a nonconducting material.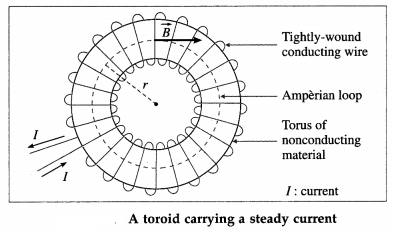

In an ideal toroid carrying a steady current, the magnetic field in the interior of the toroid is tangential to any circle concentric with the axis of the toroid and has the same value on this circle (the dashed line in figure). Also, the magnitude of the magnetic induction external to the toroid is negligible.