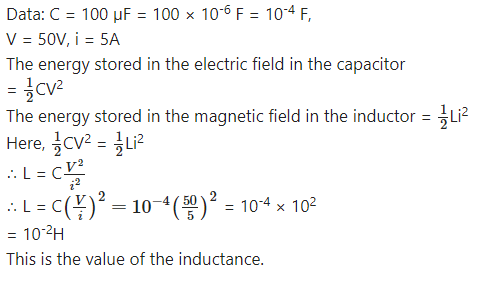Maharashtra Board Class 12 Physics Solutions Chapter 13 AC Circuits

1. Choose the correct option.

iii) In a circuit L, C & R are connected in series with an alternating voltage of frequency f. the current leads the voltage by 450. The value of C is

Answer:

(A) 106W
(B) 150W
(C) 5625W
(D) Zero
Answer:
(C) 5625W

v) In a series LCR circuit the phase difference between the voltage and the current is 45°. Then the power factor will be
(A) 0.607
(B) 0.707
(C) 0.808
(D) 1
Answer:
(B) 0.707

2. Answer in brief.

i) An electric lamp is connected in series with a capacitor and an AC source is glowing with a certain brightness. How does the brightness of the lamp change on increasing the capacitance ?
Answer:

ii) The total impedance of a circuit decreases when a capacitor is added in series with L and R. Explain why ?
Answer:

iii) For very high frequency AC supply, a capacitor behaves like a pure conductor. Why ?
Answer:

iv) What is wattless current ?
Answer:
The current that does not lead to energy consumption, hence zero power consumption, is called wattless current.
In the case of a purely inductive circuit or a purely capacitive circuit, average power consumed over a complete cycle is zero and hence the corresponding alternating current in the circuit is called wattless current.
[Note : In this case, the power factor is zero.]

v) What is the natural frequency of L C circuit ? What is the reactance of this circuit at this frequency
Answer:

where L is the inductance and C is the capacitance. The reactance of this circuit at this frequency is

Question 3.
In a series LR circuit X_L = R and power factor of the circuit is P₁. When capacitor with capacitance C such that X_L = X_C is put in series, the power factor becomes P₂. Calculate P₁ / P₂ .
Answer:
For a series LR circuit, power factor,

Question 4.
When an AC source is connected to an ideal inductor show that the average power supplied by the source over a complete cycle is zero.
Answer:

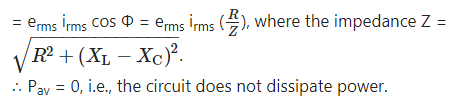
Question 5.
Prove that an ideal capacitor in an AC circuit does not dissipate power
Answer:

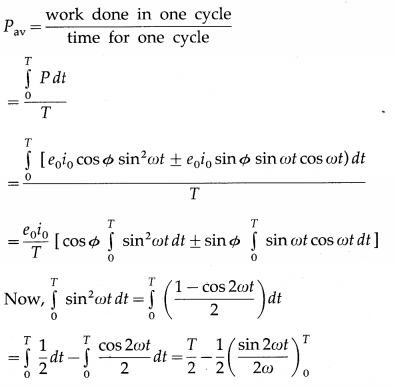
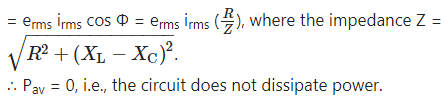
Question 6.
(a) An emf e = e₀ sin ωt applied to a series L – C – R circuit derives a current I = I₀ sinωt in the circuit. Deduce the expression for the average power dissipated in the circuit.
(b) For circuits used for transporting electric power, a low power factor implies large power loss in transmission. Explain.
Answer:
(a) Instantaneous power,
P = ei
= (e₀ sin ωt) [i₀ (sin ωt ± Φ)]
= e₀i₀ sin ωt(sin ωt cos Φ ± cos ωt sin Φ)
= e₀i₀ sin² ωt ± e₀i₀ sin Φ sin ωt cos ωt
Average power over one cycle,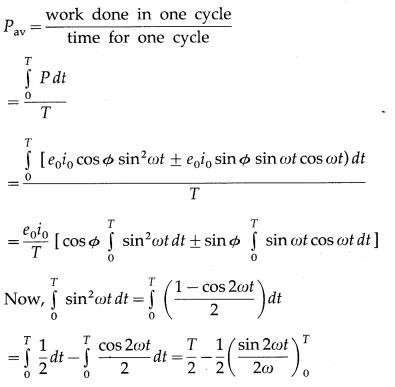

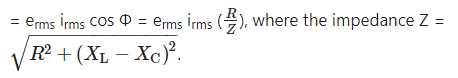
(b) P_av = e_rms i_rms cos Φ
The factor cos Φ is called as power factor. For circuits used for transporting electric power, a low power factor means the power available on transportation is much less than e_rms i_rms It means there is significant loss of power during transportation.

Question 7.
A device Y is connected across an AC source of emf e = e₀ sinωt. The current through Y is given as i = i₀ sin(ωt + π/2)
a) Identify the device Y and write the expression for its reactance.
b) Draw graphs showing variation of emf and current with time over one cycle of AC for Y.
c) How does the reactance of the device Y vary with the frequency of the AC ? Show graphically
d) Draw the phasor diagram for the device Y.
Answer:

where ω is the angular frequency of the applied emf and C is the capacitance of the capacitor.

(b)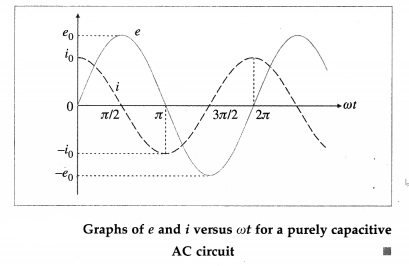

(d)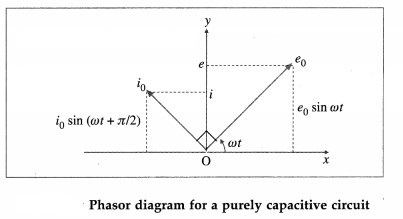

The phasor representing the peak emf (e₀) makes an angle (ωt) in an anticlockwise direction with respect to the horizontal axis. As the current leads the voltage by 90°, the phasor representing the peak current (i₀) is turned 90° anticlockwise with respect to the phasor representing emf e₀. The projections of these phasors on the vertical axis give instantaneous values of e and i.

Question 8.
Derive an expression for the impedance of an LCR circuit connected to an AC power supply.
Answer:
Figure shows an inductor of inductance L, capacitor of capacitance C, resistor of resistance R, key K and source (power supply) of alternating emf (e) connected to form a closed series circuit.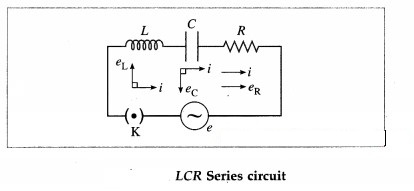



is the effective resistance of the circuit. It is called the impedance.

Question 9.
Compare resistance and reactance.
Answer:
(1) Resistance is opposition to flow of charges (current) and appears in a DC circuit as well as in an AC circuit.
The term reactance appears only in an AC circuit. It occurs when an inductor and/or a capacitor is used.

(2) In a purely resistive circuit, current and voltage are always in phase.
When reactance is not zero, there is nonzero phase difference between current and voltage.

(3) Resistance does not depend on the frequency of AC.
Reactance depends on the frequency of AC. In case of an inductor, reactance increases linearly with frequency. In case of a capacitor, reactance decreases as frequency of AC increases; it is inversely proportional to frequency.

(4) Resistance gives rise to production of Joule heat in a component.
In a circuit with pure reactance, there is no production of heat.

Question 10.
Show that in an AC circuit containing a pure inductor, the voltage is ahead of current by π/2 in phase.
Answer:
Figure 13.8 shows an AC source, generating a voltage e = e₀ sin ωt, connected to a key K and a pure inductor of inductance L to form a closed circuit.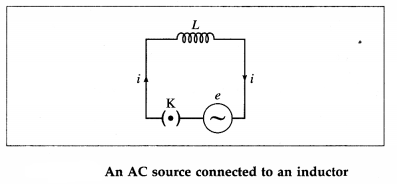

On closing the key K, an emf is induced in the inductor as the magnetic flux linked with it changes with time. This emf opposes the applied emf and according to the laws of electromagnetic induction by Faraday and Lenz, we have,

where e’ is the induced emf and i is the current through the inductor. To maintain the current; e and e’ must be equal in magnitude and opposite in direction.

According to Kirchhoff’s voltage law, as the resistance of the inductor is assumed to be zero, we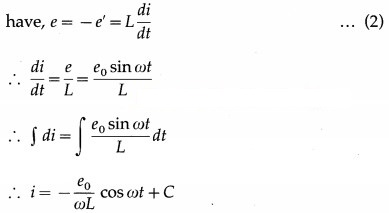

where C is the constant of integration. C must be time independent and have the dimension of current. As e oscillates about zero, i also oscillates about zero and hence there cannot be any time independent component of current.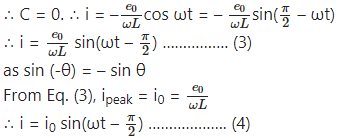

Comparison of this equation with e = e₀ sin ωt shows that e leads i by   rad, i.e., the voltage is ahead of current by   rad in phase.

Question 11.
An AC source generating a voltage e = e₀ sinωt is connected to a capacitor of capacitance C. Find the expression for the current i flowing through it. Plot a graph of e and i versus ωt.
Answer:
Figure 13.12 shows an AC source, generating a voltage e = e₀ sin ωt, connected to a capacitor of capacitance C. The plates of the capacitor get charged due to the applied voltage. As the alternating voltage is reversed in each half cycle, the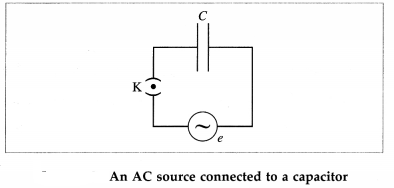



Table gives the values of e and i for different values of cot and Fig shows graphs of e and i versus ωt. i leads e by phase angle of  rad.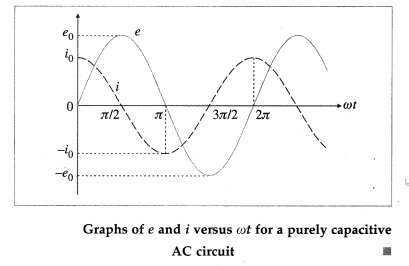

Question 12.
If the effective current in a 50 cycle AC circuit is 5 A, what is the peak value of current? What is the current 1/600 sec.after if was zero ?
Answer:

Question 13.
A light bulb is rated 100W for 220 V AC supply of 50 Hz. Calculate (a) resistance of the bulb. (b) the rms current through the bulb.
Answer: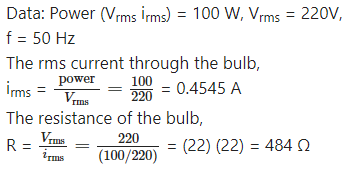

Question 14.
A 15.0 µF capacitor is connected to a 220 V, 50 Hz source. Find the capacitive reactance and the current (rms and peak)
in the circuit. If the frequency is doubled, what will happen to the capacitive reactance and the current.
Answer:

If the frequency is doubled, the capacitive reactance will be halved and the current will be doubled.

Question 15.
An AC circuit consists of only an inductor of inductance 2 H. If the current is represented by a sine wave of amplitude 0.25 A and frequency 60 Hz, calculate the effective potential difference across the inductor (π = 3.142)
Answer:

Question 16.
Alternating emf of e = 220 sin 100 πt is applied to a circuit containing an inductance of (1/π) henry. Write an equation for instantaneous current through the circuit. What will be the reading of the AC galvanometer connected in the circuit?
Answer:

Question 17.
A 25 µF capacitor, a 0.10 H inductor and a 25Ω resistor are connected in series with an AC source whose emf is given by e = 310 sin 314 t (volt). What is the frequency, reactance, impedance, current and phase angle of the circuit?
Answer:
Data: C = 25 µF = 25 × 10^-6F, L = 0.10H, R = 25 Ω ,
e = 310 sin (314 t) [volt]
Comparing e = 310 sin (314 t) with
e = e₀ sin (2πft), we get,
the frequency of the alternating emf as

Question 18.
A capacitor of 100 µF, a coil of resistance 50Ω and an inductance 0.5 H are connected in series with a 110 V-50Hz source. Calculate the rms value of current in the circuit.
Answer:
Data : C = 100 µF = 100 × 10^-6 F = 10^-4 F,
R = 50 Ω, L = 0.5H, f = 50 Hz, V_rms = 110 V
∴ ωL = 2πfL = 2 (3.142)(50)(0.5) = 157.1 Ω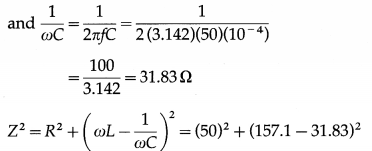

Question 19.
Find the capacity of a capacitor which when put in series with a 10Ω resistor makes the power factor equal to 0.5. Assume an 80V-100Hz AC supply.
Answer: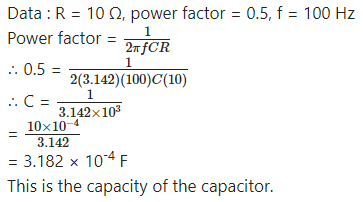

Question 20.
Find the time required for a 50 Hz alternating current to change its value from zero to the rms value.
Answer: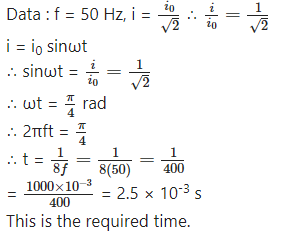

Question 21.
Calculate the value of capacitance in picofarad, which will make 101.4 micro henry inductance to oscillate with frequency of one megahertz.
Answer:
Data : f_r = 10⁶ Hz, L = 101.4 × 10^-6 H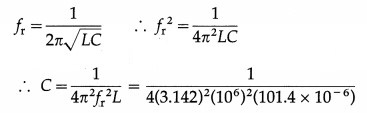

= 10000×10−104(3.142)2(101.4) = 2.497 × 10^-10 F
= 249.7 × 10^-12 F = 249.7 picofarad
This is the value of the capacity.

Question 22.
A 10 µF capacitor is charged to a 25 volt of potential. The battery is disconnected and a pure 100 m H coil is connected across the capacitor so that LC oscillations are set up. Calculate the maximum current in the coil.
Answer:

Question 23.
A 100 µF capacitor is charged with a 50 V source supply. Then source supply is removed and the capacitor is connected across an inductance, as a result of which 5A current flows through the inductance. Calculate the value of the inductance.
Answer: