Maharashtra Board Class 12 Physics Solutions Chapter 6 Superposition of Waves

Chapter 6 Superposition of Waves

1. Choose the correct option.

i) When an air column in a pipe closed at one end vibrates such that three nodes are formed in it, the frequency of its
vibrations is …….times the fundamental frequency.
(A) 2
(B) 3
(C) 4
(D) 5
Answer:
(D) 5

ii) If two open organ pipes of length 50 cm and 51 cm sounded together produce 7 beats per second, the speed of sound is.
(A) 307 m/s
(B) 327m/s
(C) 350m/s
(D) 357m/s
Answer:
(D) 357m/s

iii) The tension in a piano wire is increased by 25%. Its frequency becomes ….. times the original frequency.
(A) 0.8
(B) 1.12
(C) 1.25
(D) 1.56
Answer:
(B) 1.12

iv) Which of the following equations represents a wave travelling along the y-axis?
(A) x = A sin(ky – ωt)
(B) y = A sin(kx – ωt)
(C) y = A sin(ky) cos(ωt)
(D) y = A cos(ky)sin(ωt)
Answer:
(A) x = A sin(ky – ωt)

v) A standing wave is produced on a string fixed at one end with the other end free. The length of the string
(A) must be an odd integral multiple of λ/4.
(B) must be an odd integral multiple of λ/2.
(C) must be an odd integral multiple of λ.
(D) must be an even integral multiple ofλ.
Answer:
(A) must be an odd integral multiple of λ/4.

2. Answer in brief.

i) A wave is represented by an equation y = A sin (Bx + Ct). Given that the constants A, B and C are positive, can you tell in which direction the wave is moving?
Answer:
The wave is travelling along the negative x-direction.

ii) A string is fixed at the two ends and is vibrating in its fundamental mode. It is known that the two ends will be at rest. Apart from these, is there any position on the string which can be touched so as not to disturb the motion of the string? What will be the answer to this question if the string is vibrating in its first and second overtones?
Answer:
Nodes are the points where the vibrating string can be touched without disturbing its motion.
When the string vibrates in its fundamental mode, the string vibrates in one loop. There are no nodes formed between the fixed ends. Hence, there are no point on the string which can be touched without disturbing its motion.

When the string vibrates in its first overtone (second harmonic), there are two loops of the stationary wave on the string. Apart from the two nodes at the two ends, there is now a third node at its centre. Hence, the string can be touched at its centre without disturbing the stationary wave pattern.

When the string vibrates in its second overtone (third harmonic), there are three loops of the stationary wave on the string. So, apart from the two end nodes, there are two additional nodes in between, at distances one-third of the string length from each end. Thus, now the string can be touched at these two nodes.

iii) What are harmonics and overtones?
Answer:
A stationary wave is set up in a bounded medium in which the boundary could be a rigid support (i.e., a fixed end, as for instance a string stretched between two rigid supports) or a free end (as for instance an air column in a cylindrical tube with one or both ends open). The boundary conditions limit the possible stationary waves and only a discrete set of frequencies is allowed.

The lowest allowed frequency, n₁, is called the fundamental frequency of vibration. Integral multiples of the fundamental frequency are called the harmonics, the fundamental frequency being the fundamental or 2n₁, the third harmonic is 3n₁, and so on.

The higher allowed frequencies are called the overtones. Above the fundamental, the first allowed frequency is called the first overtone, the next higher frequency is the second overtone, and ‘so on. The relation between overtones and allowed harmonics depends on the system under consideration.

iv) For a stationary wave set up in a string having both ends fixed, what is the ratio of the fundamental frequency to the
second harmonic?
Answer:
The fundamental is the first harmonic. Therefore, the ratio of the fundamental frequency (n) to the second harmonic (n₁) is 1 : 2.

(a) wavelength,
(b) frequency and
(c) amplitude of the wave. [(a) 0.4 m (b) 25 Hz (c) 0.2 m]
Answer:

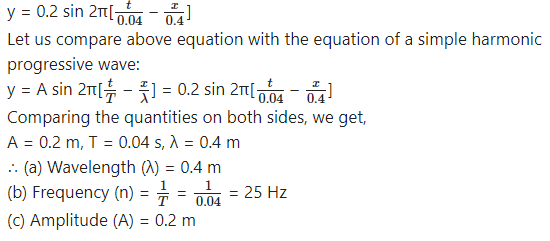
Question 3.
State the characteristics of progressive waves.
Answer:
Characteristics of a progressive wave :

1. Energy is transmitted from particle to particle without the physical transfer of matter.
2. The particles of the medium vibrate periodically about their equilibrium positions.
3. In the absence of dissipative forces, every particle vibrates with the same amplitude and frequency, but differs in phase from its adjacent particles. Every particle lags behind in its state of motion compared to the one before it.
4. A wave motion is doubly periodic, i.e., it is periodic in time and periodic in space.
5. The velocity of propagation through a medium depends upon the properties of the medium.
6. Progressive waves are of two types : transverse and longitudinal. In a transverse mechanical wave, the individual particles of the medium vibrate perpendicular to the direction of propagation of the wave. The progressively changing phase of the successive particles results in the formation of alternate crests and troughs that are periodic in space and time. In an em wave, the electric and magnetic fields oscillate in mutually perpendicular directions, perpendicular to the direction of propagation.
   In a longitudinal mechanical wave, the individual particles of the medium vibrate along the line of propagation of the wave. The progressively changing phase of the successive particles results in the formation of typical alternate regions of compressions and rarefactions that are periodic in space and time. Periodic compressions and rarefactions result in periodic pressure and density variations in the medium. There are no longitudinal em wave.
7. A transverse wave can propagate only through solids, but not through liquids and gases while a longitudinal wave can propagate through any material medium.

Question 4.
State the characteristics of stationary waves.
Answer:
Characteristics of stationary waves :

1. Stationary waves are produced by the interference of two identical progressive waves travelling in opposite directions, under certain conditions.
2. The overall appearance of a standing wave is of alternate intensity maximum (displacement antinode) and minimum (displacement node).
3. The distance between adjacent nodes (or antinodes) is λ/2.
4. The distance between successive node and antinode is λ/4.
5. There is no progressive change of phase from particle to particle. All the particles in one loop, between two adjacent nodes, vibrate in the same phase, while the particles in adjacent loops are in opposite phase.
6. A stationary wave does not propagate in any direction and hence does not transport energy through the medium.
7. In a region where a stationary wave is formed, the particles of the medium (except at the nodes) perform SHM of the same period, but the amplitudes of the vibrations vary periodically in space from particle to particle.

[Note : Since the nodes are points where the particles are always at rest, energy cannot be transmitted across a node. The energy of the particles within a loop remains localized, but alternates twice between kinetic and potential energy during each complete vibration. When all the particles are in the mean position, the energy is entirely kinetic. When they are in their extreme positions, the energy is entirely potential.]

Question 5.
Derive an expression for equation of stationary wave on a stretched string.
Answer:
When two progressive waves having the same amplitude, wavelength and speed propagate in opposite directions through the same region of a medium, their superposition under certain conditions creates a stationary interference pattern called a stationary wave.

Consider two simple harmonic progressive waves, of the same amplitude A, wavelength A and frequency n = ω/2π, travelling on a string stretched along the x-axis in opposite directions. They may be represented by
y₁ = A sin (ωt – kx) (along the + x-axis) and … (1)
y₂ = A sin (ωt + kx) (along the – x-axis) …. (2)
where k = 2π/λ is the propagation constant.

By the superposition principle, the resultant displacement of the particle of the medium at the point at which the two waves arrive simultaneously is the algebraic sum

Question 6.
Find the amplitude of the resultant wave produced due to interference of two waves given as y₁ = A₁ sin ωt y₂ = A₂ sin (ωt + φ)
Answer:
The amplitude of the resultant wave produced due to the interference of the two waves is

Question 7.
State the laws of vibrating strings and explain how they can be verified using a sonometer.
Answer:
The fundamental is the first harmonic. Therefore, the ratio of the fundamental frequency (n) to the second harmonic (n₁) is 1 : 2.

Question 8.
Show that only odd harmonics are present in the vibrations of air column in a pipe closed at one end.
Answer:
Consider a narrow cylindrical pipe of length l closed at one end. When sound waves are sent down the air column in a cylindrical pipe closed at one end, they are reflected at the closed end with a phase reversal and at the open end without phase reversal. Interference between the incident and reflected waves under appropriate conditions sets up stationary waves in the air column.

The stationary waves in the air column in this case are subject to two boundary conditions that there must be a node at the closed end and an antinode at the open end.

Taking into account the end correction e at the open end, the resonating length of the air column is L = l + e.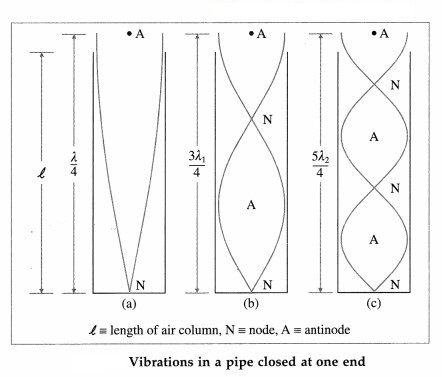

Let v be the speed of sound in air. In the simplest mode of vibration, there is a node at the closed end and an antinode at the open end. The distance between a node and a consecutive anti-node is λ4, where λ is the wavelength of sound. The corresponding wavelength λ and frequency n are

This gives the fundamental frequency of vibration and the mode of vibration is called the fundamental mode or first harmonic.

In the next higher mode of vibration, the first overtone, two nodes and two antinodes are formed. The corresponding wavelength λ₁ and frequency n₁ are

Therefore, the frequency in the first overtone is three times the fundamental frequency, i.e., the first overtone is the third harmonic.

In the second overtone, three nodes and three antinodes are formed. The corresponding wavelength λ₂ and frequency n₂ are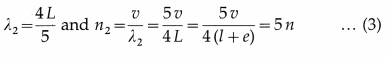

which is the fifth harmonic.
Therefore, in general, the frequency of the pth overtone (p = 1, 2, 3, ,..) is
n_p = (2p + 1)n … (4)
i.e., the pth overtone is the (2p + 1)th harmonic.

Equations (1), (2) and (3) show that allowed frequencies in an air column in a pipe closed at one end are n, 3n, 5n, …. That is, only odd harmonics are present as overtones.

Question 9.
Prove that all harmonics are present in the vibrations of the air column in a pipe open at both ends.
Answer:
Consider a cylindrical pipe of length l open at both the ends. When sound waves are sent down the air column in a cylindrical open pipe, they are reflected at the open ends without a change of phase. Interference between the incident and reflected waves under appropriate conditions sets up stationary waves in the air column.

The stationary waves in the air column in this case are subject to the two boundary conditions that there must be an antinode at each open end.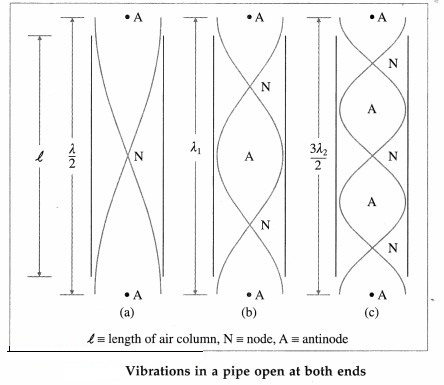

Taking into account the end correction e at each of the open ends, the resonating length of the air column is L = l + 2e.

Let v be the speed of sound in air. In the simplest mode of vibration, the fundamental mode or first harmonic, there is a node midway between the two antinodes at the open ends. The distance between two consecutive antinodes is λ/2, where λ is the wavelength of sound. The corresponding wavelength λ and the fundamental frequency n are

In the next higher mode, the first overtone, there are two nodes and three antinodes. The corresponding wavelength λ₁ and frequency n₁

i.e., twice the fundamental. Therefore, the first overtone is the second harmonic.

Therefore, in general, the frequency of the pth overtone (p = 1, 2, 3, …) is
n_p = (p + 1)n … (4)
i.e., the pth overtone is the (p + 1)th harmonic.
Equations (1), (2) and (3) show that allowed frequencies in an air column in a pipe open at both ends are n, 2n, 3n, …. That is, all the harmonics are present as overtones.

Question 10.
A wave of frequency 500 Hz is travelling with a speed of 350 m/s.
(a) What is the phase difference between two displacements at a certain point at times 1.0 ms apart?
(b) what will be the smallest distance between two points which are 45º out of phase at an instant of time?
[Ans : π, 8.75 cm ]
Answer:

Question 11.
A sound wave in a certain fluid medium is reflected at an obstacle to form a standing wave. The distance between two successive nodes is 3.75 cm. If the velocity of sound is 1500 m/s, find the frequency. [Ans : 20 kHz]
Answer: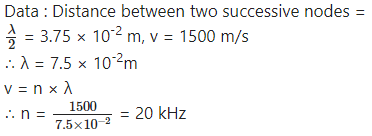

Question 12.
Two sources of sound are separated by a distance 4 m. They both emit sound with the same amplitude and frequency (330 Hz), but they are 180º out of phase. At what points between the two sources, will the sound intensity be maximum? (Take velocity of sound to be 330 m/s) [Ans: ± 0.25, ± 0.75, ± 1.25 and ± 1.75 m from the point at the center]

Question 13.
Two sound waves travel at a speed of 330 m/s. If their frequencies are also identical and are equal to 540 Hz, what will be the phase difference between the waves at points 3.5 m from one source and 3 m from the other if the sources are in phase? [Ans : 1.636 π]
Answer:

Question 14.
Two wires of the same material and same cross-section are stretched on a sonometer. One wire is loaded with 1.5 kg and another is loaded with 6 kg. The vibrating length of first wire is 60 cm and its fundamental frequency of vibration is the same as that of the second wire. Calculate vibrating length of the other wire. [Ans: 1.2 m]
Answer:
Data : m₁ = m₂ = m, L₁ = 60 cm = 0.6 m, T₁ = 1.5 kg = 14.7 N, T₂ = 6 kg = 58.8 N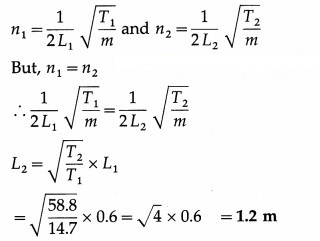

The vibrating length of the second wire is 1.2 m.

Question 15.
A pipe closed at one end can produce overtones at frequencies 640 Hz, 896 Hz and 1152 Hz. Calculate the fundamental
frequency. [Ans: 128 Hz]
Answer:
The difference between the given frequencies of the overtones is 256 Hz. This implies that they are consecutive overtones. Let n_C be the fundamental frequency of the closed pipe and n_q, n_q-1, n_q-1 = the frequencies of the q^th, (q + 1)^th and (q + 2)^th consecutive overtones, where q is an integer.

Data : n_q = 640 Hz, n_q-1 = 896 Hz, n_q+2 = 1152 Hz
Since only odd harmonics are present as overtones, n_q = (2q +1) n_C
and n_q+1 = [2(q + 1) + 1] n_C = (2q + 3) n_C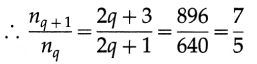

∴ 14q + 7 = 10q + 15 ∴ 4q = 8 ∴ q = 2
Therefore, the three given frequencies correspond to the second, third and fourth overtones, i.e., the fifth, seventh and ninth harmonics, respectively.
∴ 5n_C = 640 ∴ b_C = 128Hz

Question 16.
A standing wave is produced in a tube open at both ends. The fundamental frequency is 300 Hz. What is the length of tube in the fundamental mode? (speed of the sound = 340 m s^-1). [Ans: 0.5666 m]
Answer:
Data : For the tube open at both the ends, n = 300 Hz and v = 340 m / s Igonoring end correction, the fundamental frequency of the tube is

The length of the tube open at both the ends is 0.5667 m.

Question 17.
Find the fundamental, first overtone and second overtone frequencies of a pipe, open at both the ends, of length 25 cm if the speed of sound in air is 330 m/s. [Ans: 660 Hz, 1320 Hz, 1980 Hz]
Answer:
Data : Open pipe, ∠25 cm = 0.25 m, v = 330 m / s
The fundamental frequency of an open pipe ignoring end correction,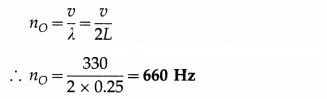

Since all harmonics are present as overtones, the first overtone is, n₁ = 2n₀ = 2 × 660 = 1320 Hz
The second overtone is n₂ = 3n = 3 × 660 = 1980 Hz

Question 18.
A pipe open at both the ends has a fundamental frequency of 600 Hz. The first overtone of a pipe closed at one end has the same frequency as the first overtone of the open pipe. How long are the two pipes? (Take velocity of sound to be 330 m/s) [Ans : 27.5 cm, 20.625 cm]
Answer:

Question 19.
A string 1m long is fixed at one end. Transverse vibrations of frequency 15 Hz are imposed at the free end. Due to this, a stationary wave with four complete loops, is produced on the string. Find the speed of the progressive wave which produces the stationary wave.[Hint: Remember that the free end is an antinode.] [Ans: 6.67 m s^-1]
Answer:

Question 20.
A violin string vibrates with fundamental frequency of 440Hz. What are the frequencies of first and second overtones? [Ans: 880 Hz, 1320 Hz]
Answer:
Data: n =440Hz
The first overtone, n₁ = 2n =2 × 400 = 880 Hz
The second overtone, n₁ = 3n = 3 × 400 = 1320 Hz

Question 21.
A set of 8 tuning forks is arranged in a series of increasing order of frequencies. Each fork gives 4 beats per second with the next one and the frequency of last for k is twice that of the first. Calculate the frequencies of the first and the last for k. [Ans: 28 Hz, 56 Hz]
Answer:
Data : n₈ = 2n₁, beat frequency = 4 Hz
The set of tuning fork is arranged in the increasing order of their frequencies.
∴ n₂ = n₁ + 4
n₃ = n₂ + 4 = n₁ + 2 × 4
n₄ = n₃ + 4 = n₁ + 3 × 4
∴ n₈ = n₇ + 4 = n₁ + 7 × 4 = n₁ + 28
Since n₈ = 2n₁,
2n₁ = n₁ + 28
∴ The frequency of the first fork, n₁ = 28 Hz
∴ The frequency of the last fork,
n₈ = n₁ + 28 = 28 + 28 = 56 Hz

Question 22.
A sonometer wire is stretched by tension of 40 N. It vibrates in unison with a tuning fork of frequency 384 Hz. How
many numbers of beats get produced in two seconds if the tension in the wire is decreased by 1.24 N? [Ans: 12 beats]
Answer:
Data : T₁ =40N, n₁ = 384 Hz, T₂ = 40 – 1.24 = 38.76 N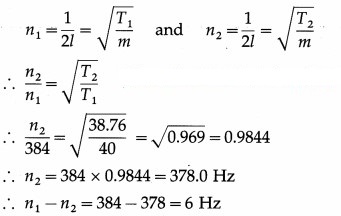

∴ The number of beats produced in two seconds = 2 × 6 = 12

Question 23.

Question 24.
The string of a guitar is 80 cm long and has a fundamental frequency of 112 Hz. If a guitarist wishes to produce a frequency of 160 Hz, where should the person press the string? [Ans : 56 cm from one end]
Answer:
Data : L₁ = 80 cm n₁ = 112 Hz, n₂ = 160 Hz
According to the law of length, n₁L₁ = n₂L₂.
∴ The vibrating length to produce the fundamental frequency of 160 Hz,

Questions and Answers

Can you tell? (Textbook Page No. 132)

Question 1.
What is the minimum distance between any two particles of a medium which always have the same speed when a sinusoidal wave travels through the medium ?
Answer:
When a sinusoidal wave travels through a medium the minimum distance between any two particles of the medium which always have the same speed is .
Such particles are opposite in phase, i.e., their instantaneous velocities are opposite in direction.
[Note : The minimum distance between any two particles which have the same velocity is λ]

Do you know? (Textbook Page No. 140)

Question 1.
What happens if a simple pendulum is pulled aside and released ?
Answer:
If a simple pendulum is pulled aside and released, it oscillates freely about its equilibrium position at its natural frequency which is inversely proportional to the square root of its length and directly proportional to the square root of the acceleration of gravity at the place. These oscillations, called as free oscillations, are periodic and tautochronous if the displacement of its bob is small and the dissipative forces can be ignored.

Question 2.
What happens when a guitar string is plucked ?
Answer:
When a guitar string is plucked, two wave pulses of the same amplitude, frequency and phase move out from that point towards the fixed ends of the string where they get reflected. For certain ratios of wavelength to length of the string, these reflected pulses moving towards each other will meet in phase to form standing waves on the string. The vibrations of the string cause the air molecules to oscillate, forming sound waves that radiate away from the string. The frequency of the sound waves is equal to the frequency of the vibrating string. In general, the wavelengths of the sound waves and the waves on the string are different because their speeds in the two mediums are not the same.

Question 3.
Have you noticed vibrations in a drill machine or in a washing machine ? How do they differ from vibrations in the above two cases ?
Answer:
Vibrations in the body of a drill machine or that of a washing machine are forced vibrations induced by the vibrations of the motors of these machines. On the other hand, the oscillations of a simple pendulum or a guitar string are free oscillations, produced when they are disturbed from their equilibrium position and released.

Question 4.
A vibrating tuning fork of certain frequency is held in contact with a tabletop and its vibrations are noticed and then another vibrating tuning fork of different frequency is held on the tabletop. Are the vibrations produced in the tabletop the same for both the tuning forks ? Why ?
Answer:
No. Because the tuning forks have different frequencies, the forced vibrations in the tabletop differ both in frequency and amplitude. The tuning fork whose frequency is closer to a natural frequency of the tabletop induces forced vibrations of a larger amplitude.