Question 1. Each equation is followed by the values of the variable. Decide whether these values are the solutions of that equation.
i. x – 4 = 3, x = – 1, 7, – 7
ii. 9m = 81, m = 3, 9, -3
iii. 2a + 4 = 0, a = 2, – 2, 1
iv. 3 – y = 4, y = – 1, 1, 2
Solution:
i. x – 4 = 3 ….(i)
Substituting x = – 1 in L.H.S. of equation (i),
L.H.S. = (-1) – 4
= – 5
R.H.S. = 3
∴ L.H.S. ≠ R.H.S.
∴ x = – 1 is not the solution of the given equation.
Substituting x = 7 in L.H.S. of equation (i),
L.H.S. = (7) – 4
= 3
R.H.S. = 3
∴ L.H.S. = R.H.S.
∴ x = 7 is the solution of the given equation.
Substituting x = – 7 in L.H.S. of equation (i),
L.H.S. = (- 7) – 4
= -11
R.H.S. = 3
∴ L.H.S. ≠ R.H.S.
∴ x = – 7 is not the solution of the given equation.
ii. 9m = 81 …(i)
Substituting m = 3 in L.H.S. of equation (i),
L.H.S. = 9 × (3)
= 27
R.H.S. = 81
∴L.H.S. ≠ R.H.S.
∴m = 3 is not the solution of the given equation.
Substituting m = 9 in L.H.S. of equation (i),
L.H.S. = 9 × (9)
= 81
R.H.S. = 81
∴L.H.S. = R.H.S.
∴m = 9 is the solution of the given equation.
Substituting m = – 3 in L.H.S. of equation (i),
L.H.S. = 9 × (- 3)
= -27
R.H.S. = 81
∴L.H.S. ≠ R.H.S.
∴m = – 3 is not the solution of the given equation.
iii. 2a + 4 = 0 …..(i)
Substituting a = 2 in L.H.S. of equation (i),
L.H.S. = 2 (2) + 4
= 4 + 4
= 8
R.H.S. = 0
∴L.H.S. ≠ R.H.S.
∴a = 2 is not the solution of the given equation.
Substituting a = – 2 in L.H.S. of equation (i),
L.H.S. = 2 (-2)+ 4
= -4 + 4
= 0
R.H.S. = 0
∴L.H.S. = R.H.S.
∴a = – 2 is the solution of the given equation.
Substituting a = 1 in L.H.S. of equation (i),
L.H.S. = 2(1)+ 4
= 2 + 4
= 6
R.H.S. = 0
∴ L.H.S. ≠ R.H.S.
∴a = 1 is not the solution of the given equation.
iv. 3 – y = 4 …(i)
Substituting y = -1 in L.H.S. of equation (i),
L.H.S. = 3 – (- 1)
= 3 + 1
= 4
R.H.S. = 4
∴L.H.S. = R.H.S.
∴y = – 1 is the solution of the given equation.
Substituting y = 1 in L.H.S. of equation (i),
L.H.S. = 3-(1)
= 2
R.H.S. = 4
∴L.H.S. ≠ R.H.S.
∴y = 1 is not the solution of the given equation.
Substituting y = 2 in L.H.S. of equation (i),
L.H.S. = 3-(2)
= 1
R.H.S. = 4
∴L.H.S. ≠ R.H.S.
∴y = 2 is not the solution of the given equation.
Question 2.
Solve the following equations: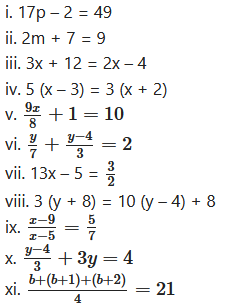
Solution:
i. 17p – 2 = 49
∴ 17p – 2 + 2 = 49 + 2
…[Adding 2 on both the sides]
∴ 17p = 51![]()
p = 3
ii. 2m + 7 = 9
∴ 2m + 7 – 7 = 9 – 7
…[Subtracting 7 from both the sides]
∴ 2m = 2![]()
∴ m = 1
iii. 3x + 12 = 2x – 4
∴ 3x + 12 – 12 = 2x – 4 – 12
…[Subtracting 12 from both the sides]
∴ 3x = 2x – 16
∴ 3x – 2x = 2x – 16 – 2x
…[Subtracting 2x from both the sides]
∴ x = – 16
iv. 5 (x – 3) = 3 (x + 2)
∴ 5x – 15 = 3x + 6
∴ 5x – 15 + 15 = 3x + 6 + 15
…[Adding 15 on both the sides]
∴ 5x = 3x + 21
∴ 5x – 3x = 3x + 21 – 3x
…[Subtracting 3x from both the sides]
∴ 2x = 21

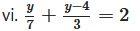


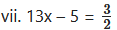

viii. 3 (y + 8) = 10 (y – 4) + 8
∴ 3y + 24 = 10y – 40 + 8
∴ 3y + 24 = 10y – 32
∴ 3y + 24 – 24 = 10y – 32 – 24
…[Subtracting 24 from both the sides]
∴ 3y = 10y – 56
∴ 3y – 10y = 10y – 56
…[Subtracting 10y from both the sides]
∴ – 7y = – 56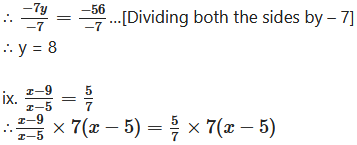
…[Multiplying both the sides by 7 (x – 5)]
∴7 (x – 9) = 5 (x – 5)
∴7x – 63 = 5x – 25
∴7x – 63 + 63 = 5x – 25 + 63
…[Adding 63 on both the sides]
∴7x = 5x + 38
∴7x – 5x = 5x + 38 – 5x
…[Subtracting 5x from both the sides]
∴ 2x = 38
…[Multiplying both the sides by 4]
∴b + b + 1 + b + 2 = 84
∴3b + 3 = 84
∴3b + 3 – 3 = 84 – 3
…[ Subtracting 3 from both the sides]
∴3b = 81
∴\(\frac{3 b}{3}=\frac{81}{3}[/latex …[Dividing both the sides by 3]
∴b = 27
Intext Questions and Activities
Question 1.
Fill in the boxes to solve the following equations. (Textbook pg. no. 75)
i. x + 4 = 9
∴x + 4 – __ = 9 – __
… [Subtracting 4 from both the sides]
∴ x = __
ii. x – 2 = 7
∴x – 2 + __ = 7 + __
… [Adding 2 on both the sides]
∴x = __
iii. [latex]\frac { x }{ 3 }=4\)
∴ × __ = 4 ×__
∴x = __
iv. 4x = 24
∴ __ = __
∴x = __
Solution:
i. x + 4 = 9
∴x + 4 – 4 = 9 – 4
… [Subtracting 4 from both the sides]
∴ x = 5
ii. x – 2 = 7
∴x – 2 + 2 = 7 + 2
… [Adding 2 on both the sides]
∴x = 9
iii. x/3=4
∴x/3× 3 = 4 × 3
… [Multiplying both the sides by 3]
∴x = 12
iv. 4x = 24![]()
… [Dividing both the sides by 4]
∴x = 6
