Question 1.
In each pair of triangles in the following figures, parts bearing identical marks are congruent. State the test and correspondence of vertices by which triangles in each pair are congruent.
i.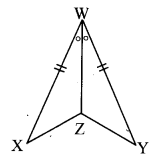
ii.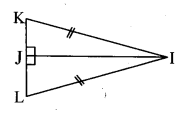
iii.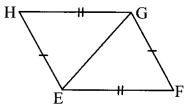
iv.
v.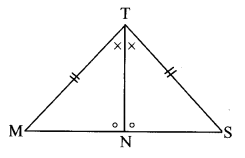
Solution:
i.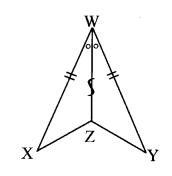
The two triangles are congruent by SAS test in the correspondence XWZ ↔ YWZ.
ii.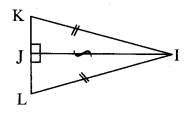
The two triangles are congruent by hypotenuse-side test in the correspondence KJI ↔ LJI.
iii.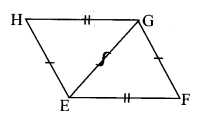
The two triangles are congruent by SSS test in the correspondence HEG ↔ FGE.
iv.
The two triangles are congruent by ASA test is the correspondence SMA ↔ OPT.
v.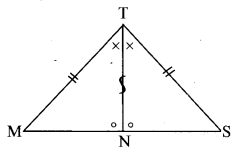
The two triangles are congruent by ASA test or SAS test or SAA test in the correspondence MTN ↔ STN.
Intext Questions and Activities
Question 1.
Write answers to the following questions referring to the given figure.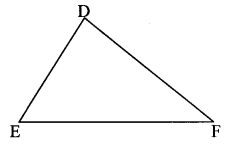
- Which is the angle opposite to the side DE?
- Which is the side opposite to ∠E?
- Which angle is included by side DE and side DF?
- Which side is included by ∠E and ∠F?
- State the angles adjacent to side DE. (Textbook pg, no. 81)
Solution:
- ∠DFE i.e. ∠F is the angle opposite to side DE.
- Side DF is the side opposite to ∠E.
- ∠EDF i.e. ∠D is included by side DE and side DF.
- Side EF is included by ∠E and ∠F.
- ∠DEF and ∠EDF i.e. ∠E and ∠D are adjacent to side DE.
Question 2.
In the given figure, parts of triangles indicated by identical marks are congruent.
a. Identify the one-to-one correspondence of vertices in which the two triangles are congruent and write the congruence.
b. State with reason, whether the statement, ∆XYZ ≅ ∆STU is right or wrong. (Textbook pg. no. 82)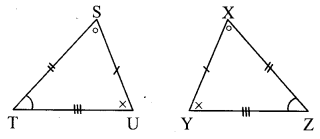
Solution:
a. From the figure,
S ↔ X, T ↔ Z, U ↔ Y i.e.,
STU ↔ XZY, or SUT ↔ XYZ, or
TUS ↔ ZYX, or TSU ↔ ZXY, or
UTS ↔ YZX, or UST ↔ YXZ
∴ ∆STU ≅ ∆XZY, or ∆SUT ≅ ∆XYZ, or
∆TUS ≅ ∆ZYX, or ∆TSU ≅ ∆ZXY, or
∆UTS ≅ ∆YZX, or ∆UST ≅ ∆YXZ
b. If ∆XYZ ≅ ∆STU, then
∠Y ≅ ∠T, ∠Z ≅ ∠U,
seg XY ≅ seg ST, seg XZ ≅ seg SU
∴ But, all the above statements are wrong. The statement AXYZ ≅ ASTU is wrong.
