Question 1. On the construction work of a flyover bridge there were 320 workers initially. The number of workers were increased by 25% every year. Find the number of workers after 2 years.
Solution:
Here, P = Initial number of workers = 320
R = Increase in the number of workers per year = 25%
N = 2 years
A = Number of workers after 2 years
∴ The number of workers after 2 years would be 500.
Question 2.
A shepherd has 200 sheep with him. Find the number of sheeps with him after 3 years if the increase in number of sheeps is 8% every year.
Solution:
Here, P = Present number of sheeps = 200
R = Increase in number of sheeps per year = 8%
N = 3 years
A = Number of sheeps after 3 years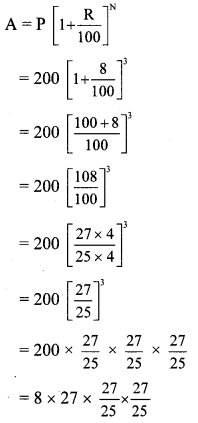
= ×27×27×27
= 0.0128 × 27 × 27 × 27
= 251.9424
= 252
∴ The number of sheeps with the shepherd after 2 years would be 252 (approx).
Question 3.
In a forest there are 40,000 trees. Find the expected number of trees after 3 years if the objective is to increase the number at the rate 5% per year.
Solution:
Here, P = Present number of trees in the forest = 40,000
R = Increase in the number of trees per year = 5%
N = 3 years
A = Number of trees after 3 years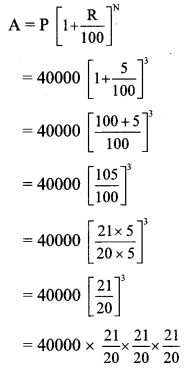
= 5 × 21 × 21 × 21
= 5 × 9261
= 46,305
∴ The expected number of trees in the forest after 3 years is 46,305.
Question 4.
The cost price of a machine is Rs 2,50,000. If the rate of depreciation is 10% per year, find the depreciation in price of the machine after two years.
Solution:
Here, P = Cost price of machine = Rs 2,50,000
R = Rate of depreciation per year = 10%
N = 2 years
A = Depreciated price of the machine after 2 years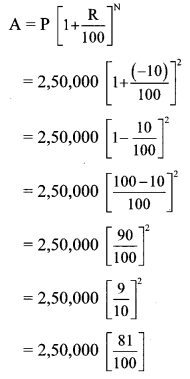
= 2,500 × 81
= Rs 2,02,500
Depreciation in price = Cost price (P) – Depreciated price (A)
= 2,50,000 – 2,02,500
= Rs 47,500
∴ The depreciation in price of the machine after 2 years would be Rs 47,500.
Question 5.
Find the compound interest if the amount of a certain principal after two years is Rs 4036.80 at the rate of 16 p.c.p.a.
Solution:
Here, A = Rs 4036.80, R = 16 p.c.p.a. and N = 2 years![]()

ii. Interest = Amount (A) – Principal (P)
= 4036.80 – 3000
= Rs 1036.80
∴ The compound interest after 2 years would be Rs 1036.80.
Question 6.
A loan of Rs 15,000 was taken on compound interest. If the rate of compound interest is 12 p.c.p.a. find the amount to settle the loan after 3 years.
Solution:
Here, P = Rs 15,000, R = 12 p.c.p.a, and
N = 3 years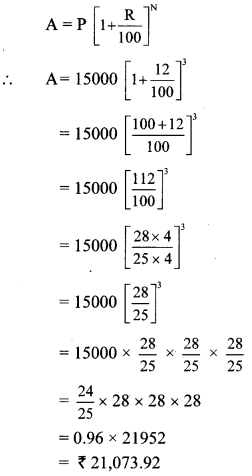
∴ The amount required to settle the loan after 3 years is Rs 21,073.92.
Question 7.
A principal amounts to Rs 13,924 in 2 years by compound interest at 18 p.c.p.a. Find the principal.
Solution:
Here, A = Rs 13,924, R = 18 p.c.p.a., and N = 2 years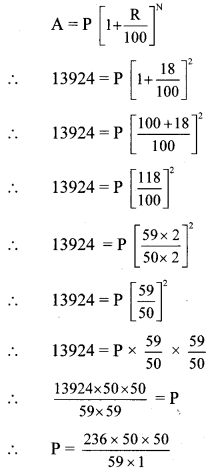
∴ P = 4 x 50 x 50
∴ P = Rs 10,000
∴ The principal is Rs 10,000.
Question 8.
The population of a suburb is 16,000. Find the rate of increase in the population if the population after two years is 17,640.
Solution:
Here, P = Population of a suburb = 16,000
N = 2 years
A = Increase in the population after 2 years = 17,640
R = Rate of increase in population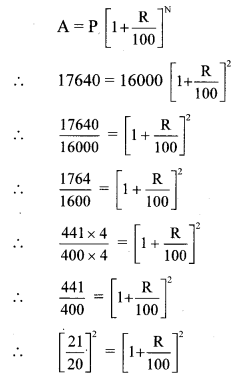

∴5 = R
i.e., R = 5%
∴The rate of increase in the population is 5 p.c.p.a.
Compound Interest Practice Set 14.2 Question 9.
In how many years Rs 700 will amount to Rs 847 at a compound interest rate of 10 p.c.p.a.
Solution:
Here, P = Rs 700, R = 10 p.c.p.a., A = Rs 847
∴Rs 700 will amount to Rs 847 in 2 years.
Question 10.
Find the difference between simple interest and compound interest on Rs 20,000 in 2 years at 8 p.c.p.a.
Solution:
Here, P = Rs 20,000, R = 8 p.c.p.a.,
N = 2 years
i. Simple interest (I)
Simple interest (I) = Rs 3200
ii. Compound Interest (I):
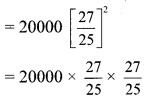
= 32 × 27 × 27
= Rs 23,328
Compound interest (I)
= Amount (A) – Principal (P)
= 23,328 – 20,000
= Rs 3328 ,..(ii)
iii. Difference
= Compound interest – Simple interest
= 3328 – 3200 … [Form (i) and (ii)]
= Rs 128
∴ The difference between compound interest and simple interest is Rs 128.
[Note: The question is modified as per the answer given in the textbook.]
Intext Questions and Activities
Question 1.
Visit the bank nearer to your house and get the information regarding the different schemes and rates of interests. Make a chart and display in your class. (Textbook pg. no. 90)
Solution:
(Students should attempt this activity at their own.)
