Question 1.
Find the volume of the cylinder if height (h) and radius of the base (r) are as given below.
i. r = 10.5 cm, h = 8 cm
ii. r = 2.5 m, h = 7 m
iii. r = 4.2 cm, h = 5 cm
iv. r = 5.6 cm, h = 5 cm
Solution:
i. Given: r = 10.5 cm and h = 8 cm
To find: Volume of the cylinder
Volume of the cylinder = πr²h
= 22/7x 10.5 x 10.5 x 8
= 22 x 1.5 x 10.5 x 8
= 2772 cc
∴ The volume of the cylinder is 2772 cc.
ii. Given: r = 2.5 m and h = 7 m
To find: Volume of the cylinder
Volume of the cylinder = πr²h
= 22/7x 2.5 x 2.5 x 7
= 22 x 2.5 x 2.5
= 137.5 cu.m
∴ The volume of the cylinder is 137.5 cu.m.
iii. Given: r = 4.2 cm and h = 5 cm
To find: Volume of the cylinder
Volume of the cylinder = πr²h
= 22/7x 4.2 x 4.2 x 5
= 22 x 0.6 x 4.2 x 5
= 277.2 cc
∴ The volume of the cylinder is 277.2 cc.
iv. Given: r = 5.6 cm and h = 5 cm
To find: Volume of the cylinder
Volume of the cylinder = πr²h
= 22/7 x 5.6 x 5.6 X 5 7
= 22 x 0.8 x 5.6 x 5
= 492.8 cc
∴ The volume of the cylinder is 492.8 cc.


Question 4.
Find the volume of the cylinder if the circumference of the base of cylinder is 132 cm and height is 25 cm.
Solution:
Given: Circumference of the base of cylinder = 132 cm and height (h) = 25 cm
To find: Volume of the cylinder
i. Circumference of base of cylinder = 2πr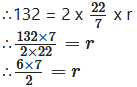
∴3 x 7 = r
∴r = 21 cm
ii. Volume of the cylinder = πr²h
= 22/7 x 21 x 21 x 25
= 22 x 3 x 21 x 25
= 34650 cc
∴ The volume of the cylinder is 34650 cc.
Intext Questions and Activities
Question 1.
Leonard Euler, discovered an interesting formula regarding the faces, vertices and edges of solid figures.
Count and write the faces, vertices and edges of the following figures and complete the table. From the table verify Euler’s formula, F + V = E + 2. (Textbook pg. No. 113)
Solution: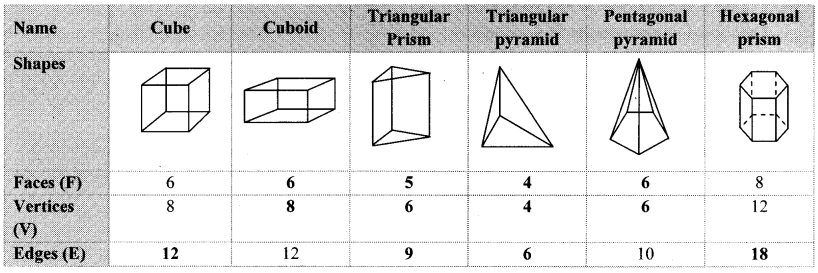
From the above table, F + V = E + 2 i.e. Euler’s formula is verified.
