Question 1.
The information about number of workers and number of days to complete a work is given in the following table. Complete the table.
| Number of workers | 30 | 20 | __ | 10 | __ |
| Days | 6 | 9 | 12 | 36 |
Solution:
Let, n represent the number of workers and d represent the number of days required to complete a work.
Since, number of workers and number of days to complete a work are in inverse poportion.
∴ n∝1/d
∴ n=k×1/d
where k is the constant of variation.
∴ n × d = k …(i)
i. When n = 30, d = 6
∴ Substituting n = 30 and d = 6 in (i), we get
n × d = k
∴ 30 × 6 = k
∴ k = 180
Substituting k = 180 in (i), we get
∴ n × d = k
∴ n × d = 180 …(ii)
This is the equation of variation
ii. When d = 12, n = 7
∴ Substituting d = 12 in (ii), we get
n × d = 180
∴ n × 12 = 180
∴ n = 180/12
∴ n = 15
iii. When n = 10, d = ?
∴ Substituting n = 10 in (ii), we get
n × d = 180
10 × d = 180
∴ d = 180/10
∴ d = 18
iv. When d = 36, n = ?
∴ Substituting d = 36 in (ii), we get
n × d = 180
∴ n × 36 = 180
∴ n = 180/36
∴ n = 5
| Number of workers | 30 | 20 | 15 | 10 | 5 |
| Days | 6 | 9 | 12 | 18 | 36 |
Question 2.
Find constant of variation and write equation of variation for every example given below: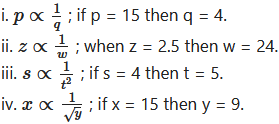
Solution:
i. p∝1q …[Given]
∴ p = k × 1/q
where, k is the constant of variation.
∴ p × q = k …(i)
When p = 15, q = 4
∴ Substituting p = 15 and q = 4 in (i), we get
p × q = k
∴ 15 × 4 = k
∴ k = 60
Substituting k = 60 in (i), we get
p × q = k
∴ p × q = 60
This is the equation of variation.
∴ The constant of variation is 60 and the equation of variation is pq = 60.
ii. z∝1w …[Given]
∴ z = k × 1/w
where, k is the constant of variation,
∴ z × w = k …(i)
When z = 2.5, w = 24
∴ Substituting z = 2.5 and w = 24 in (i), we get
z × w = k
∴ 2.5 × 24 = k
∴ k = 60
Substituting k = 60 in (i), we get
z × w = k
∴ z × w = 60
This is the equation of variation.
∴ The constant of variation is 60 and the equation of variation is zw = 60.
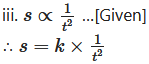
where, k is the constant of variation,
∴ s × t² = k …(i)
When s = 4, t = 5
∴ Substituting, s = 4 and t = 5 in (i), we get
s × t² = k
∴ 4 × (5)² = k
∴ k = 4 × 25
∴ k = 100
Substituting k = 100 in (i), we get
s × t² = k
∴ s × t² = 100
This is the equation of variation.
∴ The constant of variation is 100 and the equation of variation is st² = 100.
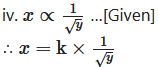
where, k is the constant of variation,
∴ x × √y = k …(i)
When x = 15, y = 9
∴ Substituting x = 15 and y = 9 in (i), we get
x × √y = k
∴ 15 × √9 = k
∴ k = 15 × 3
∴ k = 45
Substituting k = 45 in (i), we get
x × √y = k
∴ x × √y = 45 .
This is the equation of variation.
∴ The constant of variation is k = 45 and the equation of variation is x√y = 45.
Question 3.
The boxes are to be filled with apples in a heap. If 24 apples are put in a box then 27 boxes are needed. If 36 apples are filled in a box how many boxes will be needed?
Solution:
Let x represent the number of apples in each box and y represent the total number of boxes required.
The number of apples in each box are varying inversely with the total number of boxes.
∴ x∞1/y
∴ x=k×1/y
where, k is the constant of variation,
∴ x × y = k …(i)
If 24 apples are put in a box then 27 boxes are needed.
i.e., when x = 24, y = 27
∴ Substituting x = 24 and y = 27 in (i), we get
x × y = k
∴ 24 × 27 = k
∴ k = 648
Substituting k = 648 in (i), we get
x × y = k
∴ x × y = 648 …(ii)
This is the equation of variation.
Now, we have to find number of boxes needed
when, 36 apples are filled in each box.
i.e., when x = 36,y = ?
∴ Substituting x = 36 in (ii), we get
x × y = 648
∴ 36 × y = 648
∴ y = 648/36
∴ y = 18
∴ If 36 apples are filled in a box then 18 boxes are required.
Question 4.
Write the following statements using symbol of variation.
- The wavelength of sound (l) and its frequency (f) are in inverse variation.
- The intensity (I) of light varies inversely with the square of the distance (d) of a screen from the lamp.
Solution:
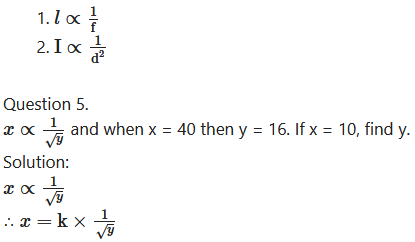
where, k is the constant of variation.
∴ x × √y = k …(i)
When x = 40, y = 16
∴ Substituting x = 40 andy = 16 in (i), we get
x × √y = k
∴ 40 × √16 = k
∴ k = 40 × 4
∴ k = 160
Substituting k = 160 in (i), we get
x × √y = k
∴ x × √y = 160 …(ii)
This is the equation of variation.
When x = 10,y = ?
∴ Substituting, x = 10 in (ii), we get
x × √y = 160
∴ 10 × √y = 160
∴ √y = 160/10
∴ √y = 16
∴ y = 256 … [Squaring both sides]
Question 6.
x varies inversely as y, when x = 15 then y = 10, if x = 20, then y = ?
Solution:
Given that,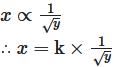
where, k is the constant of variation.
∴ x × y = k …(i)
When x = 15, y = 10
∴ Substituting, x = 15 and y = 10 in (i), we get
x × y = k
∴ 15 × 10 = k
∴ k = 150
Substituting, k = 150 in (i), we get
x × y = k
∴ x × y = 150 …(ii)
This is the equation of variation.
When x = 20, y = ?
∴ substituting x = 20 in (ii), we get
x × y = 150
∴ 20 × y = 150
∴ y = 150/20
∴ y = 7.5
