Question 1.
Measures of opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of its each angle.
Solution:
Let ₹PQRS be the parallelogram.
m∠Q = (3x – 2)° and m∠S = (50 – x)°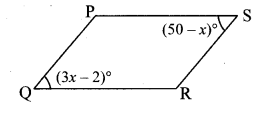
m∠Q = m∠S
…..(i)
[Opposite angles of a parallelogram are congruent]
∴ 3x – 2 = 50 – x
∴ 3x + x = 50 + 2
∴ 4x = 52
∴ x = 52/4
∴ x = 13
Now, m∠Q = (3x – 2)°
= (3 x 13 – 2)° = (39 – 2)° = 37°
∴ m∠S = m∠Q = 37° …[From(i)]
m∠P + m∠Q = 180°
….[Adjacent angles of a parallelogram are supplementary]
∴ m∠P + 37° = 180°
∴ m∠P = 180° – 37° = 143°
∴ m∠R = m∠P = 143°
…..[Opposite angles of a parallelogram are congruent]
∴ The measures of the angles of the parallelogram are 37°, 143°, 37° and 143°.
Question 2.
Referring the given figure of a parallelogram, write the answers of questions given below.
i. If l(WZ) = 4.5 cm, then l(XY) = ?
ii. If l(YZ) = 8.2 cm, then l(XW) = ?
iii. If l(OX) = 2.5 cm, then l(OZ) = ?
iv. If l(WO) = 3.3 cm, then l(WY) = ?
v. If m∠WZY = 120°, then m∠WXY = ? and m∠XWZ = ?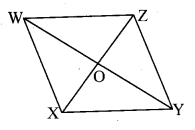
Solution:
i. l(WZ) = 4.5 cm … [Given]
l(X Y) = l(WZ) ….[Opposite sides of a parallelogram are congrument ]
∴ l(X Y) = 4.5cm
ii. l(YZ) = 8.2 cm …[Given]
l(XW) = l(YZ)
…[Opposite sides of a parallelogram are congruent]
∴ l(XW) = 8.2cm … [Given]
iii. l(OX) = 2.5 cm …[Given]
l(OZ) = l(OX)
….[Diagonals of a parallelogram bisect each other]
∴ l(OZ) = 2.5cm

v. m∠WZY =120° … [Given]
m∠WXY = m∠WZY
…..[Opposite angles of a parallelogram are congrument]
∴ m∠WXY = 120° …(i)
m∠XWZ + m∠WXY = 180°
….[Adjacent angles of a parallelogram are supplementary]
∴ m∠XWZ + 120° = 180° … [From (i)]
∴ m∠XWZ = 180°- 120°
∴ m∠XWZ = 60°
Question 3.
Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40°, l(AB) = 3 cm
Solution: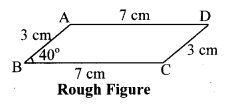
Opposite sides of a parallelogram are congruent.
∴ l(AB) = l(CD) = 3cm
l(BC) = l(AD) = 7 cm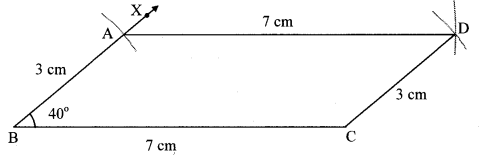
Question 4.
Ratio of consecutive angles of a quadrilateral is 1 : 2 : 3 : 4. Find the measure of its each angle. Write with reason, what type of a quadrilateral it is.
Solution:
Let ₹PQRS be the quadrilateral.
Ratio of consecutive angles of a quadrilateral is 1 : 2 : 3 : 4.
Let the common multiple be x.
∴m∠P = x°, m∠Q = 2x°, m∠R = 3x° and m∠S = 4x°
In ₹PQRS,
m∠P + m∠Q + m∠R + m∠S = 360°
…[Sum of the measures of the angles of a quadrilateral is 360°]
∴x° + 2x° + 3x° + 4x° = 360°
∴10 x° = 360°
∴x° = 360/10
∴x° = 36°
∴m∠P = x° = 36°
m∠Q = 2x° = 2 × 36° = 72°
m∠R = 3x° = 3 × 36° = 108° and
m∠S = 4x° = 4 × 36° = 144°
∴The measures of the angles of the quadrilateral are 36°, 72°, 108°, 144°.
Here, m∠P + m∠S = 36° + 144° = 180°
Since, interior angles are supplementary,
∴side PQ || side SR
m∠P + m∠Q = 36° + 72° = 108° ≠ 180°
∴side PS is not parallel to side QR.
Since, one pair of opposite sides of the given quadrilateral is parallel.
∴The given quadrilateral is a trapezium.
Question 5.
Construct ₹BARC such that
l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
Solution: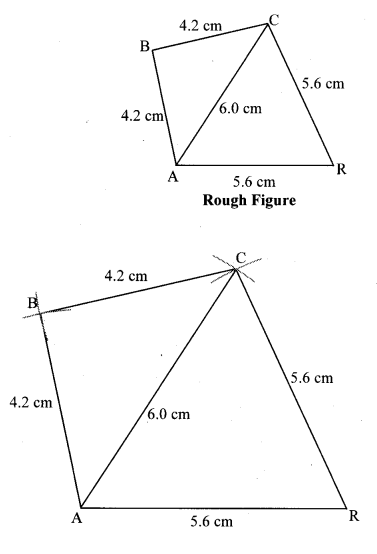
Question 6.
Construct ₹PQRS, such that l(PQ) = 3.5 cm, l(QR) = 5.6 cm, l(RS) = 3.5 cm, m∠Q = 110°, m∠R = 70°. If it is given that ₹PQRS is a parallelogram, which of the given information is unnecessary?
Solution: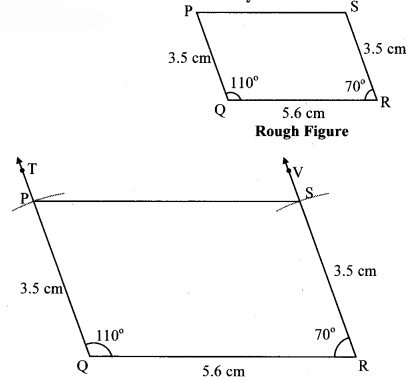
- Since, the opposite sides of a parallelogram are congruent.
∴ Either l(PQ) or l(SR) is required. - To construct a parallelogram lengths of adjacent sides and measure of one angle is required.
∴ Either l(PQ) and m∠Q or l(SR) and m∠R is the unnecessary information given in the question.
Intext Questions and Activities
Question 1.
Draw a parallelogram PQRS. Take two rulers of different widths, place one ruler horizontally and draw lines along its edges. Now place the other ruler in slant position over the lines drawn and draw lines along its edges. We get a parallelogram. Draw the diagonals of it and name the point of intersection as T.
- Measure the opposite angles of the parallelogram.
- Measure the lengths of opposite sides.
- Measure the lengths of diagonals.
- Measure the lengths of parts of the diagonals made by point T. (Textbook pg. no. 47)
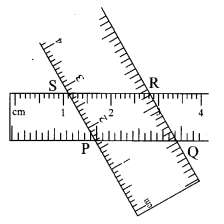
Solution:
[Students should attempt the above activities on their own.]
Question 2.
In the given figure of ₹ABCD, verify with a divider that seg AB ≅ seg CB and seg AD ≅ seg CD. Similarly measure ∠BAD and ∠BCD and verify that they are congruent. (Textbook pg. no. 48)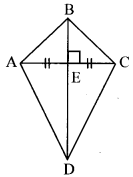
Solution:
[Students should attempt the above activities on their own.]
