Question 1.
Choose the correct option.
If arc AXB and arc AYB are corresponding arcs and m(arc AXB) = 120° then m(arc AYB) =
(A) 140°
(B) 60°
(C) 240°
(D) 160°
Solution:
(C) 240°
Hint:
Measure of major arc = 360° – measure of corresponding minor arc
∴ m (arc AYB) = 360 – m (arc AXB)
∴ m (arc AYB) = 360 – 120
∴ m (arc AYB) = 240°
Question 2.
Some arcs are shown in the circle with centre ‘O’ Write the names of the minor arcs, major arcs and semicircular arcs from among them.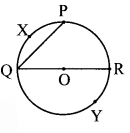
Solution:
Minor arcs : arc QXP, arc PR, arc RY, arc YQ, arc QX, arc XP, arc PRY.
Major arcs : arc PYQ, arc PQR, arc RQY, arc XPQ, arc XQP, arc XQR
Semicircular arcs : arc QPR, arc QYR.
Question 3.
In a circle with centre O, the measure of a minor arc is 110°. What is the measure of the major arc PYQ?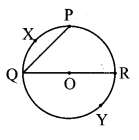
Solution:
Measure of major arc = 360° – measure of corresponding minor arc
∴ m (arc PYQ) = 360 – 110
∴ m (arc PYQ) = 250°
∴ The measure of the major arc PYQ is 250°.
Intext Questions and Activities
Question 1.
Measure the circumference and diameter of the objects given below and enter the ratio of the circumference to its diameter in the table.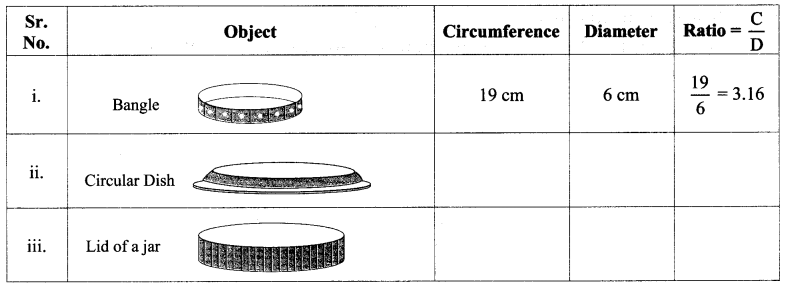
Examine the ratio of the circumference to the diameter. What do we see? (Textbook pg. no. 75)
Solution:
The ratio of circumference to the diameter is same and is approximately equal to 3.14.
Question 2.
Place a cylindrical bottle on a paper and trace the outline of its base. Use a thread to measure the circumference of the circle. (Textbook pg. no. 75)
Solution:
(Students should attempt the above activities on their own)
Question 3.
Measure the circumference of a bangle with the help of a thread. (Textbook pg. no. 75)
Solution:
(Students should attempt the above activities on their own)
Question 4.
Measure the circumference of any cylindrical object using a thread. (Textbook pg. no. 75)
Solution:
(Students should attempt the above activities on their own)
