Chapter 1 Similarity Set 1.3

Question 1.
In the adjoining figure, ∠ABC = 75°, ∠EDC = 75°. State which two triangles are similar and by which test? Also write the similarity of these two triangles by a proper one to one correspondence.

Solution:
In ∆ABC and ∆EDC,
∠ABC ≅ ∠EDC [Each angle is of measure 75°]
∠ACB ≅ ∠ECD [Common angle]
∴ ∆ABC ~ ∆EDC [AA test of similarity]
One to one correspondence is
ABC ↔ EDC

Question 2.
Are the triangles in the adjoining figure similar? If yes, by which test?

Solution:

Question 3.
As shown in the adjoining figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m, then how long will be the shadow of the bigger pole at the same time?

Solution:
Here, AC and PR represents the bigger and smaller poles, and BC and QR represents their shadows respectively.
Now, ∆ACB – ∆PRQ [ ∵ Vertical poles and their shadows form similar figures]

∴ x = 12 m
∴ The shadow of the bigger pole will be 12 metres long at that time.

Question 4.
In ∆ABC, AP ⊥ BC, BQ ⊥ AC, B – P – C, A – Q – C, then prove that ∆CPA – ∆CQB. If AP = 7, BQ = 8, BC = 12, then find AC.

Solution:
In ∆CPA and ∆CQB,
∠CPA ≅ ∠CQB [Each angle is of measure 90°]
∠ACP ≅ ∠BCQ [Common angle]
∴ ∆CPA ~ ∆CQB [AA test of similarity]

Question 5.
Given: In trapezium PQRS, side PQ || side SR, AR = 5 AP, AS = 5 AQ, then prove that SR = 5 PQ.

Solution:
side PQ || side SR [Given]
and seg SQ is their transversal.
∴ ∠QSR = ∠SQP [Altemate angles]
∴ ∠ASR = ∠AQP (i) [Q – A – S]
In ∆ASR and ∆AQP,
∠ASR = ∠AQP [From (i)]
∠SAR ≅ ∠QAP [Vertically opposite angles]
∆ASR ~ ∆AQP [AA test of similarity]

Question 6.
Id trapezium ABCD (adjoining figure), side AB || side DC, diagonals AC and BD intersect in point O. If AB = 20, DC = 6, OB = 15, then find OD.

Solution:
side AB || side DC [Given]
and seg BD is their transversal.
∴ ∠DBA ≅ ∠BDC [Alternate angles]
∴ ∠OBA ≅ ∠ODC (i) [D – O – B]
In ∆OBA and ∆ODC
∠OBA ≅ ∠ODC [From (i)]
∠BOA ≅ ∠DOC [Vertically opposite angles]
∴ ∆OBA ~ ∆ODC [AA test of similarity]

Question 7.
꠸ ABCD is a parallelogram. Point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

Solution:
Proof:
꠸ ABCD is a parallelogram. [Given]
∴ side AB || side CD [Opposite sides of a parallelogram]
∴ side AT || side CD [A – B – T]
and seg DT is their transversal.
∴ ∠ATD ≅ ∠CDT [Alternate angles]
∴ ∠BTE ≅ ∠CDE (i) [A – B – T, T – E – D]
In ∆BTE and ∆CDE,
∠BTE ≅ ∠CDE [From (i)]
∠BET ≅ ∠CED [Vertically opposite angles]
∴ ∆BTE ~ ∆CDE. [AA test of similarity]
∴ TE/DE = BE/CE [Corresponding sides of similar triangles]
∴ DE × BE = CE × TE

Question 8.
In the adjoining figure, seg AC and seg BD intersect each other in point P and AP/CP = BP/DP Prove that, ∆ABP ~ ∆CDP

Solution:
Proof:
In ∆ABP and ∆CDP,
 =  [Given]
∠APB ≅ ∠CPD [Vertically opposite angles]
∴ ∆ABP ~ ∆CDP [SAS test of similarity]

Question 9.
In the adjoining figure, in ∆ABC, point D is on side BC such that, ∠BAC = ∠ADC. Prove that, CA² = CB × CD,

Solution:
Proof:
In ∆BAC and ∆ADC,
∠BAC ≅ ∠ADC [Given]
∠BCA ≅ ∠ACD [Common angle]
∴ ∆BAC ~ ∆ADC [AA test of similarity]
∴  =  [Corresponding sides of similar triangles]
∴ CA × CA = CB × CD
∴ CA² = CB × CD

Question 1.
In the adjoining figure, BP ⊥ AC, CQ ⊥ AB, A – P – C, A – Q – B, then prove that ∆APB and ∆AQC are similar. (Textbook pg. no. 20)

Solution: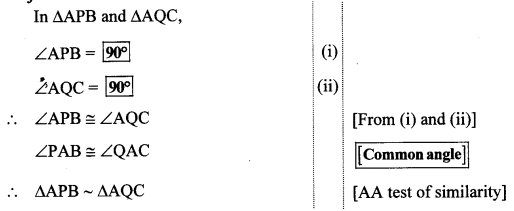

2. SAS test for similarity of triangles:
For a given correspondence, if two pairs of corresponding sides are in the same proportion and the angle between them is congruent, then the two triangles are similar.

3. SSS test for similarity of triangles:
For a given correspondence, if three sides of one triangle are in proportion with the corresponding three sides of the another triangle, then the two triangles are similar.

Properties of similar triangles:

1. Reflexivity: ∆ABC ~ ∆ABC
2. Symmetry : If ∆ABC ~ ∆DEF, then ∆DEF ~ ∆ABC.
3. Transitivity: If ∆ABC ~ ∆DEF and ∆DEF ~ ∆GHI, then ∆ABC ~ ∆GHI.