Question 1.
If n(A) = 15, n(A ∪ B) = 29, n(A ∩ B) = 7, then n(B) = ?
Solution:
Here, n(A) = 15, n(A ∪ B) = 29, n(A ∩ B) = 7
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ 29 = 15 + n(B) – 7
∴ 29 – 15 + 7 = n(B)
∴ n(B) = 21
Question 2.
In a hostel there are 125 students, out of which 80 drink tea, 60 drink coffee and 20 drink tea and coffee both. Find the number of students who do not drink tea or coffee.
Solution:
i. Let U be the set of students in the hostel, T be the set of students who drink tea and C be the set of students who drink coffee.
n(U) = 125, n(T) = 80, n(C) = 60,
number of students who drink Tea and Coffee = n(T ∩ C) = 20
ii. n(T ∪ C) = n(T) + n(C) – n(T ∩ C)
= 80 + 60 – 20
∴ n(T ∪ C) = 120
∴ 120 students drink tea or coffee
Also, there are 125 students in the hostel.
iii. Number of students who do not drink tea or coffee = n(U) – n(T ∪ C)
= 125 – 120
= 5
∴ 5 students do not drink tea or coffee.
Alternate Method:
Let U be the set of students in the hostel, T be the set of students who drink tea and C be the set of students who drink coffee.
From Venn diagram,
Student who drinks tea or coffee = n(T ∪ C) = 60 + 20 + 40 = 120
∴ The number of students who do not drink tea or coffee = n(U) – n(T ∪ C)
= 125 – 120 = 5
∴ 5 students do not drink tea or coffee.
Question 3.
In a competitive exam 50 students passed in English, 60 students passed in Mathematics and 40 students passed in both the subjects. None of them failed in both the subjects. Find the number of students who passed at least in one of the subjects ?
Solution:
Let U be the set of students who appeared for the exam,
E be the set of students who passed in English and
M be the set of students who passed in Maths.
∴ n(E) = 50, n(M) = 60,
40 students passed in both the subjects
∴ n(M ∩ E) = 40
Since, none of the students failed in both subjects
∴ Total students = n(E ∪M)
= n(E) + n(M) – n(E ∩ M)
= 50 + 60 – 40
= 70
∴ The number of students who passed at least in one of the subjects is 70.
Alternate Method:
Let U be the set of students who appeared for the exam,
E be the set of students who passed in English and M be the set of students who passed in Maths.
Since, none of the students failed in both subjects
∴ Total student = n(E ∪M)
= 10 + 40 + 20
= 70
∴ The number of students who passed at least in one of the subjects is 70.
Question 4.
A survey was conducted to know the hobby of 220 students of class IX. Out of which 130 students informed about their hobby as ’rock climbing and 180 students informed about their hobby as sky watching. There are 110 students who follow both the hobbies. Then how many students do not have any of the two hobbies? How many of them follow the hobby of rock climbing only? How many students follow the hobby of sky watching only?
Solution:
i. Let U be the set of students of class IX,
R be the set of students who follow the hobby of rock climbing and
S be the set of students who follow the hobby of sky watching.
∴ n (U) = 220, n (R) = 130, n (S) = 180,
110 students follow both the hobbies
∴ n (R ∩ S) = 110
ii. n(R ∪ S)=n (R) + n (S) – n (R ∩ S)
= 130 + 180 – 110
∴n (R ∪ S) = 200
∴ 200 students follow the hobby of rock climbing or sky watching.
iii. Total number of students = 220.
Number of students who do not follow the hobby of rock climbing or sky watching
= n (U) – n (R ∪ S)
= 220 – 200
= 20
iv. Number of students who follow the hobby of rock climbing only
= n (R) – n(R ∩ S)
= 130 – 110
= 20
v. Number of students who follow the hobby of sky watching only
= n (S) – n (R ∩ S)
= 180 – 110
= 70
Alternate Method:
Let U be the set of students of class IX,
R be the set of students who follow the hobby of rock climbing and
S be the set of students who follow the hobby of sky watching.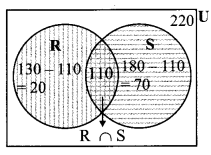
From the Venn diagram
i. Students who follow the hobby of rock climbing or sky watching
= n(R ∪ S)
= 20 + 110 + 70
= 200
ii. Number of students who do not follow the hobby of rock climbing or sky watching
= n (U) – n(R ∪S)
= 220 – 200
= 20
iii. Number of students who follow the hobby of rock climbing only
= n (R) – n(R ∩S)
= 130 – 110
= 20
iv. Number of students who follow the hobby of sky watching only
= n (S) – n (R ∩ S)
= 180 – 110
= 70
Question 5.
Observe the given Venn diagram and write the following sets.
i. A
ii. B
iii. A ∪ B
iv. U
v. A’
vi. B’
vii. (A ∪B )’
Answer:
i. A = {x, y, z, m, n}
ii. B = {p, q, r, m, n}
iii. A ∪ B = {x, y, z, m, n, p, q, r }
iv. U = {x, y, z, m, n, p, q, r, s, t}
v. A’ = {p, q, r, s, t}
vi. B’ = {x, y, z, s, t}
vii. (A ∪ B )’ = {s, t}
Question 1.
Take different examples of sets and verify the above mentioned properties. (Textbook pg.no. 12)
Solution:
i. Let A = {3, 5}, B= {3, 5, 8, 9, 10}
A ∩ B = B ∩ A = {3, 5}
ii. Let A = {3, 5}, B = {3, 5, 8, 9, 10}
Since, all elements of set A are present in set B.
∴ A ⊆ B
Also, A ∩ B = {3, 5} = A
∴ If A ⊆ B, then A ∩B = A.
iii. Let A = {2, 3, 8, 10}, B = {3,8}
A ∩ B = {3, 8} = B
Also, all the elements of set B are present in set A
∴ B ⊆ A
∴ If A ∩ B = B, then B ⊆ A.
iv. Let A = {2, 3, 8, 10}, B = {3, 8}, A ∩B = {3, 8}
Since, all the elements of set A n B are present in set A and B
A ∩ B ⊆ A and A ∩B ⊆B
v. Let U= {3, 4, 6, 8}, A = {6, 4}
∴ A’ = {3, 8}
∴ A ∩ A’= { } = φ
vi. A ∩ φ = { } = φ
vii. Let A = {6, 4}
∴ A ∩ A = {6, 4}
∴ A ∩ A = A
Question 2.
Observe the set A, B, C given by Venn diagrams and write which of these are disjoint sets. (Textbook pg. no. 12)
Solution:
Here, A = {1, 2, 3, 4, 5, 6, 7}
B = {3, 6, 8, 9, 10, 11, 12}
C = {10, 11, 12}
Now, A ∩ C = φ
∴ A and C are disjoint sets.
Question 3.
Let the set of English alphabets be the Universal set. The letters of the word ‘LAUGH’ is one set and the letter of the word ‘CRY’ is another set. Can we say that these are two disjoint sets? Observe that intersection of these two sets is empty. (Textbook pg. no. 13)
Solution:
Let A = {L, A, U, G, H}
B = {C, R, Y}
Now, A ∩ B = φ
∴ A and B are disjoint sets.
Question 4.
Fill in the blanks with elements of that set.
U = {1, 3, 5, 8, 9, 10, 11, 12, 13, 15}
A = {1,11, 13}
B = {8,5, 10, 11, 15}
A’ = { }
B’ = { }
A ∩ B = { }
A’ ∩ B’ = { }
A ∪ B = { }
A’ ∪ B’= { }
(A ∩ B)’ = { }
(A ∪ B)’ = { }
Verify: (A ∩ B)’ = A’ u B’, (A u B)’ = A’ ∩ B’ (Textbook pg. no, 18)
Solution:
U = {1, 3, 5, 8, 9, 10, 11, 12, 13, 15}
A = {1, 11, 13}
B = {8, 5, 10, 11, 15}
A’ = {3, 5, 8, 9, 10, 12, 15}
B’ = {1, 3, 9, 12, 13}
A∩ B= {11}
A’ ∩ B’= {3, 9, 12} …(i)
A ∪ B = {1, 5, 8, 10, 11, 13, 15}
A’ ∪ B’ = { 1, 3, 5, 8, 9, 10, 12, 13, 15} …(ii)
(A ∩ B)’= { 1, 3, 5, 8, 9, 10, 12, 13,15} …(iii)
(A ∪ B)’ = {3, 9, 12} ,..(iv)
(A ∩ B)’ = A’ ∪ B’ … [From (ii) and (iii)]
(A ∪ B)’ = A’ ∩ B’ … [From (i) and (iv)]
Question 5.
A = {1,2,3, 5, 7,9,11,13}
B = {1,2,4, 6, 8,12,13}
Verify the above rule for the given set A and set B. (Textbook pg. no. 14)
Solution:
A = {1, 2, 3, 5, 7, 9, 11, 13}
B = {1, 2, 4, 6, 8, 12, 13}
A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13}
A ∩ B= {1, 2, 13}
n(A) = 8, n(B) = 7,
n(A ∪ B) = 12, n(A ∩ B) = 3
n(A ∩ B) = 12 …(i)
n(A) + n(B) – n(A ∩ B) = 8 + 7 – 3 = 12 …(ii)
∴ n(A ∪ B) = n(A) + n(B) – n(A ∩ B) … [From (i) and (ii)]
Question 6.
Verify the above rule for the given Venn diagram. (Textbook pg. no. 14)
Solution:
n(A) = 5 , n(B) = 6
n(A ∪ B) = 9 , n(A ∩ B) = 2
Now, n(A ∪ B) = 9 …(i)
n(A) + n(B) – n(A ∩ B) = 5 + 6 – 2 = 9 …(ii)
∴ n(A ∪ B) = n(A) + n(B) – n(A ∩ B). …[From (i) and (ii)]
