Question 1.
Choose the correct alternative answer for each of the following questions.
i. M= {1, 3, 5}, N= {2, 4, 6}, then M ∩ N = ?
(A) {1, 2, 3, 4, 5, 6}
(B) {1, 3, 5}
(C) φ
(D) {2, 4, 6}
Answer:
(C) φ
ii. P = {x | x is an odd natural number, 1< x ≤ 5}. How to write this set in roster form?
(A) {1, 3, 5}
(B) {1, 2, 3, 4, 5}
(C) {1, 3}
(D) {3, 5}
Answer:
(D) {3, 5}
iii. P= {1, 2, ………. , 10}. What type of set Pis?
(A) Null set
(B) Infinite set
(C) Finite set
(D) None of these
Answer:
(C) Finite set
iv. M ∪ N = {1, 2, 3, 4, 5, 6} and M = {1, 2, 4}, then which of the following represent set N ?
(A) {1, 2, 3}
(B) {3, 4, 5, 6}
(C) {2, 5, 6}
(D) {4, 5, 6}
Answer:
(B) {3, 4, 5, 6}
v. If P ⊆ M, then which of the following set represent P ∩ (P ∪ M)?
(A) P
(B) M
(C) P ∪ M
(D) P’ ∩ M
Answer:
(A) P
vi. Which of the following sets are empty sets?
(A) Set of intersecting points of parallel lines.
(B) Set of even prime numbers.
(C) Month of an english calendar having less than 30 days.
(D) P = {x | x ∈ I , – 1 < x < 1}
Answer:
(A) Set of intersecting points of parallel lines.
Hints:
v. Here, P ⊆ M
∴ P ∪ M = M
∴ P ∩ (P ∪ M) = P ∩ M
= P … [∵ P ⊆M]
Question 2.
Find the correct option for the given question.
i. Which of the following collections is a set ?
(A) Colors of the rainbow
(B) Tall trees in the school campus.
(C) Rich people in the village
(D) Easy examples in the book
Answer:
(A) Colors of the rainbow
ii. Which of the following set represent N ∩W?
(A) {1, 2, 3,….}
(B) {0, 1, 2, 3,….}
(C) {0}
(D) { }
Answer:
(A) {1, 2, 3,….}
iii. P = {x | x is an odd natural number, 1< x < 5}. How to write this set in roster form?
(A) {1, 3, 5}
(B) {1, 2, 3, 4, 5}
(C) {1, 3}
(D) {3, 5}
Answer:
(B) {1, 2, 3, 4, 5}
iv. If T = {1, 2, 3, 4, 5} and M = {3,4, 7, 8}, then T ∪ M = ?
(A) {1, 2, 3, 4, 5,7}
(B) {1, 2, 3, 7, 8}
(C) {1, 2, 3, 4, 5, 7, 8}
(D) {3, 4}
Answer:
(C) {1, 2, 3, 4, 5, 7, 8}
Hints:
i. The elements of options B, C and D cannot be definitely and clearly decided.
ii. The common elements of N and W are 1 2, 3,….
Question 3.
Out of 100 persons in a group, 72 persons speak English and 43 persons speak French. Each one out of 100 persons speak at least one language. Then how many speak only English? How many speak only French ? How many of them speak English and French both?
Solution:
i. Let U be the set of all the persons,
E be the set of persons who speak English and
F be the set of persons who speak French.
∴ n(E) = 72, n(F) = 43
Since, each one out of 100 persons speak at least one language
∴ n(U) = n(E ∪ F)= 100,
ii. n (E ∪ F) = n (E) + n (F) – n(E ∩ F)
100 = 72 + 43 – n (E ∩ F)
n (E ∩ F) = 72 + 43 – 100
∴ n(E ∩ F) = 15
Number of people who speak English and French = 15
iii. Number of people who speak only English = n(E) – n(E ∩ F)
= 72 – 15 = 57
iv. Number of
people who speak only French = n(F) – n(E ∩ F)
= 43 – 15 = 28
Alternate Method:
Let U be the set of all the persons,
E be the set of persons who speak English,
F be the set of persons who speak French and x people speak both the languages.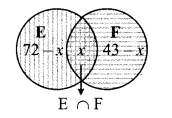
Since, each one out of 100 persons speak at least one language.
∴ n(U) = n(E ∪ F) = 100
∴ 72 – x + x + 43 – x = 100
∴ 115 – x= 100
∴ x = 115 – 100= 15.
Number of people who speak English and French = 15
Number of people who speak only English = 72 – x = 72 – 15 = 57
Number of people who speak only French = 43 – x = 43 – 15 = 28
Question 4.
70 trees were planted by Parth and 90 trees were planted by Pradnya on the occasion of Tree Plantation Week. Out of these 25 trees were planted by both of them together. How many trees were planted by Parth or Pradnya?
Solution:
i. Let P be the trees planted by Parth and Q be the trees planted by Pradnya
∴ n(P) = 70 and n(Q) = 90
Total number of trees planted by Parth and Pradnya = n(P ∩ Q) = 25
ii. Number of trees planted by Parth or Pradnya = n(P ∪ Q)
= n(P) + n(Q) – n(P ∩ Q)
= 70 + 90 – 25 = 135
∴ A total of 135 trees were planted by Parth or Pradnya.
Alternate Method:
Let P be the trees planted by Parth and Q be the trees planted by Pradnya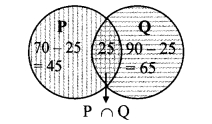
From Venn diagram
∴ Total trees planted by parth or pradnya = n(P ∪ Q)
= 45 + 25 + 65
= 135
A total of 135 trees were planted by Parth or Pradnya.
Question 5.
If n(A) = 20, n(B) = 28 and n(A ∪ B) = 36, then n(A ∩ B) = ?
Solution:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ 36 = 20 + 28 – n(A ∩ B)
∴ n(A ∩ B) = 20 + 28 – 36
∴ n(A ∩ B) = 12
Question 6.
In a class, 8 students out of 28 have a dog as their pet animal at home, 6 students have a cat as their pet animal, 10 students have dog and cat both, then how many students do not have dog or cat as their pet animal at home?
Solution:
i. Let U be the set of all the students, then n(U) = 28
Let D be the set of students who have dog as pet and C be the set of students who have cat as pet.
10 students have dog and cat as their pet animal
n(D ∩ C) = 10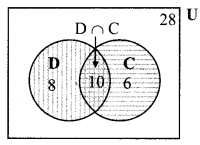
From venn diagram,
ii. Number of students who have cat or dog as pet
= n(D ∪ C)
= 8 + 10 + 6
= 24
iii. Number of students who do not have dog or cat as pet = n (U) – n(D ∪ C)
= 28 – 24
= 4
Question 7.
Represent the union of two sets by Venn diagram for each of the following.
i. A = {3, 4, 5, 7},B = {1, 4, 8} l Marks
ii. P {a, b, c, e, f, Q = {l, m, n, e, b) I Markj
iii. X = {x x is a prime number between 80 and 100}
Y = { y | y is an odd number between 90 and 100}
Solution:
i. A = {3, 4, 5, 7}, B = {1, 4, 8}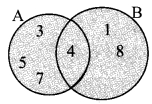
ii. P = {a, b, c, e, f}, Q = {l, m, n, e, b}
iii. X = {x | x is a prime number between 80 and 100}
∴ X = {83, 89, 97}
Y = {y | y is an odd number between 90 and 100}
∴ Y = {91, 93, 95, 97, 99}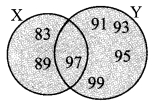
Question 8.
Write the subset relations between the following sets.
X = set of all quadrilaterals.
Y = set of all rhombuses.
S = set of all squares.
T = set of all parallelograms.
V = set of all rectangles. [3 Marks]
Solution:
i. Rhombus, square, parallelogram and rectangle all are quadrilaterals.
∴ Y ⊆ X,S ⊆ X,T ⊆ X,V ⊆ X
ii. Every square is a rhombus, parallelogram and rectangle.
∴ S ⊆ Y, S ⊆ T, S ⊆ V
iii. Every rhombus and rectangle is a parallelogram.
∴ Y ⊆ T, V ⊆ T
Question 9.
If M is any set, then write M ∪Φ and M ∩ Φ.
Solution:
Let M = {2, 3, 4, 8} and Φ = { }
∴ M ∪ Φ = {2, 3, 4, 8}
∴ M ∪ Φ = M Also, M ∩ Φ = { }
∴ M ∩ Φ = i(i
Question 10.
Observe the Venn diagram and write the given sets U, A, B, A ∪ B and A ∩ B.
U = {1,2, 3,4, 5, 7, 8, 9, 10, 11, 13}
A = {1, 2, 3, 5,7}
B = {1, 5, 8, 9, 10}
A ∪ B = {1,2, 3, 5, 7, 8, 9, 10}
A ∩ B = {1, 5}
Question 11.
If n(A) = 7, n(B) = 13, n(A ∩ B) = 4, then n(A ∪ B) = ?
Solution:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
= 7 + 13 – 4
n(A ∪ B) = 16
Question 1.
Set of students in a class and set of students in the same class who can swim, are shown by the Venn diagram.
Observe the diagram and draw Venn diagrams for the following subsets.
i. a. Set of students in a class
b. Set of students who can ride bicycles in the same class
ii. A set of fruits is given as follows.
U = {guava, orange, mango, jackfruit, chickoo, jamun, custard apple, papaya, plum}
Show these subsets.
A = fruit with one seed
B = fruit with more than one seed. (Textbook pg. no. 8)
Solution:
ii. A = {mango, jamun, plum}
B = {guava, orange, jackfruit, chickoo, custard apple, papaya}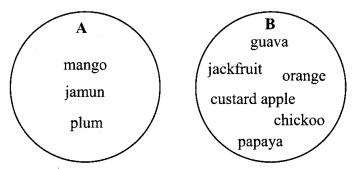
Question 2.
Every student should take 9 triangular sheets of paper and one plate. Numbers from 1 to 9 should, be written on each triangle. Everyone should keep some numbered triangles in the plate. Now the triangles in each plate form a subset of the set of numbers from 1 to 9.
Look at the plates of Sujata, Hameed, Mukta, Nandini, Joseph with the numbered triangles. Guess the thinking behind selecting these numbers. Hence write the subsets in set builder form. (Textbook pg, no. 9)
Solution:
Sujata:
S = {x | x = 2n- 1, n ∈ N, x < 9}
Hameed:
f H = {x | x = 2n, n ∈ N, x < 9}
Mukta:
M = {x | x = n2, n ∈ N, x ≤ 9}
Nandini:
N = {x | x ∈ N, x ≤ 9}
Joseph:
J = {x | x is a prime number between 1 and 9}
Question 3.
Collect the following information from 20 families nearby your house.
i. Number of families subscribing for Marathi Newspaper.
ii. Number of families subscribing for English Newspaper.
iii. Number of families subscribing for both English as well as Marathi Newspaper.
Show the collected information using Venn diagram. (Textbook pg.no. 18)
[Students should attempt the above activity on their own.]
