Question 1.
Classify the decimal form of the given rational numbers into terminating and non-terminating recurring type.
Solution:
i. Denominator = 5 = 1 x 5
Since, 5 is the only prime factor denominator.
the decimal form of the rational number 13/5 will be terminating type.
ii. Denominator = 11 = 1 x 11
Since, the denominator is other than prime factors 2 or 5.
∴ the decimal form of the rational number 2/11 will be non-terminating recurring type.
iii. Denominator = 16
= 2 x 2 x 2 x 2
Since, 2 is the only prime factor in the denominator.
∴ the decimal form of the rational number 29/16 will be terminating type.
iv. Denominator = 125
= 5 x 5 x 5
Since, 5 is the only prime factor in the denominator.
the decimal form of the rational number 17/125 will be terminating type.
v. Denominator = 6
= 2 x 3
Since, the denominator is other than prime factors 2 or 5.
∴ the decimal form of the rational number 11/6 will be non-terminating recurring type.
Question 2.
Write the following rational numbers in decimal form.
Solution:![]()
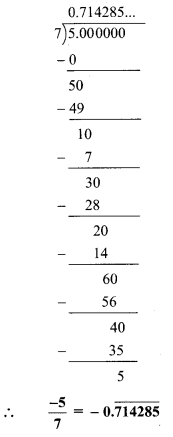

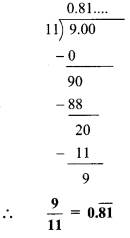
iii. √5
iv. 121/13
v. 29/8
Question 3.
Write the following rational numbers in p/q form.
Solution:
i. Let x = 0.6˙ …(i)
∴ x = 0.666…
Since, one number i.e. 6 is repeating after the decimal point.
Thus, multiplying both sides by 10,
10x = 6.666…
∴ 10 x 6.6 …(ii)
Subtracting (i) from (ii),
10x – x = 6.6 – 0.6
∴ 9x = 6

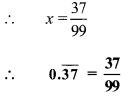

∴ 99x = 314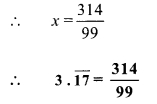




Question 1.
Solution:
Let x = 2.43
In 2.43, the number 4 on the right side of the decimal point is not recurring.
So, in order to get only recurring digits on the right side of the decimal point, we will multiply 2.43 by 10.
∴ 10x = 24.3 …(i)
∴ 10x = 24.333…
Here, digit 3 is the only recurring digit. Thus, by multiplying both sides by 10, 100x = 243.333…
∴ 100x= 243.3 …(ii)
Subtracting (i) from (ii),
100x – 10x = 243.3 – 24.3
∴ 90x = 219
