Question 1.
Question 2.
Question 3.

Question 4.
Question 5.
Find the vector equation of the line which passes through the origin and the point (5, -2, 3).
Solution:
Question 6.
Find the Cartesian equations of the line which passes through points (3, -2, -5) and (3, -2, 6).
Solution:
Let A = (3, -2, -5), B = (3, -2, 6)
The direction ratios of the line AB are
3 – 3, -2 – (-2), 6 – (-5) i.e. 0, 0, 11.
The parametric equations of the line passing through (x1, y1, z1) and having direction ratios a, b, c are
x = x1 + aλ, y = y1 + bλ, z = z1 + cλ
∴ the parametric equattions of the line passing through (3, -2, -5) and having direction ratios are 0, 0, 11 are
x = 3 + (0)λ, y = -2 + 0(λ), z = -5 + 11λ
i.e. x = 3, y = -2, z = 11λ – 5
∴ the cartesian equations of the line are
x = 3, y = -2, z = 11λ – 5, λ is a scalar.
Question 7.
Find the Cartesian equations of the line passing through A(3, 2, 1) and B(1, 3, 1).
Solution:
The direction ratios of the line AB are 3 – 1, 2 – 3, 1 – 1 i.e. 2, -1, 0.
The parametric equations of the line passing through (x1, y1, z1) and having direction ratios a, b, c are
x = x1 + aλ, y = y1 + bλ, z = z1 + cλ
∴ the parametric equattions of the line passing through (3, 2, 1) and having direction ratios 2, -1, 0 are
x = 3 + 2λ, y = 2 – λ, z = 1 + 0(λ)
x – 3 = 2λ, y – 2 = -λ, z = 1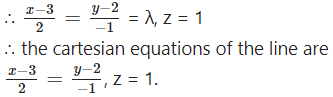
Question 8.
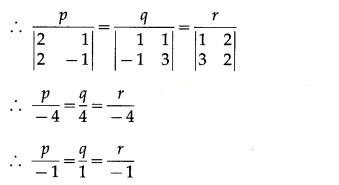
∴ the required line has direction ratios -1, 1, -1.
The cartesian equations of the line passing through (x1, y1, z1) and having direction ratios a, b, c are![]()
∴ the cartesian equations of the line passing through the point (1, 1, 2) and having direction ratios -1, 1, -1 are![]()
Question 9.
∴ p + 2q + r = 0, 3 + 2q – r = 0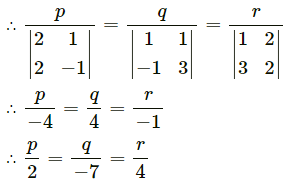
∴ the required line has direction ratios 2, -7, 4.
The cartesian equations of the line passing through (x1, y1, z1) and having direction ratios a, b, c are![]()
∴ the cartesian equation of the line passing through the point (2, -7, 4) and having directions ratios 2, -7, 4 are![]()
Question 10.
Find the vector equation of the line which passes through the origin and intersect the line x – 1 = y – 2 = z – 3 at right angle.
Solution:
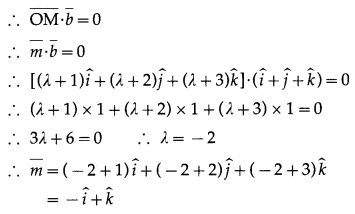

Question 11.
Solution:
The equations of the given lines are

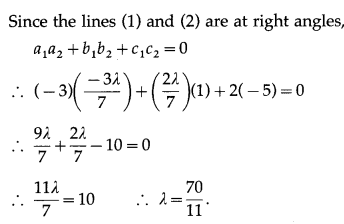
Question 12.
Solution:
Question 13.
Find the acute angle between lines x = y, z = 0 and x = 0, z = 0.
Solution:
The equations x = y, z = 0 can be written as x/1=y/1, z = 0
∴ the direction ratios of the line are 1, 1, 0.
The direction ratios of the line x = 0, z = 0, i.e., Y-axis J are 0, 1, 0.
∴ its directiton ratios are 0, 1, 0.
Let a¯ and b¯ be the vectors in the direction of the lines x = y, z = 0 and x = 0, z = 0.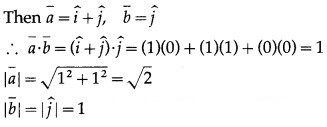
If θ is the acute angle between the lines, then
Question 14.
Find the acute angle between lines x = -y, z = 0 and x = 0, z = 0.
Solution:
The equations x = -y, z = 0 can be written as x/1=y/1, z = 0.
∴ the direction ratios of the line are 1, 1, 0.
The direction ratios of the line x = 0, z = 0, i.e., Y-axis are 0, 1, 0.
∴ its direction ratios are 0, 1, 0.
Let a¯ and b¯ be the vectors in the direction of the lines x = y, z = 0 and x = 0, z = 0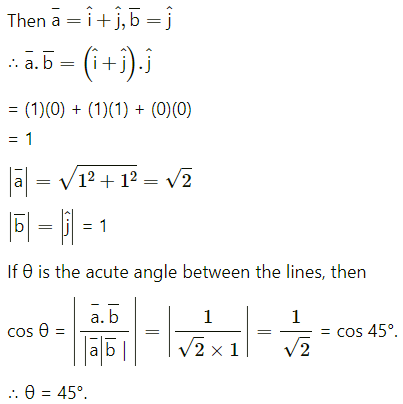
Question 15.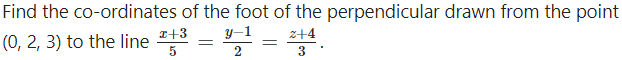
Solution:
Let P = (0, 2, 3)
Let M be the foot of the perpendicular drawn from P to the line
![]()
The coordinates of any point on the line are given by
x = 5λ – 3, y = 2λ + 1, z = 3λ – 4
Let M = (5λ – 3, 2λ + 1, 3λ – 4) …(1)
The direction ratios of PM are
5λ – 3 – 0, 2λ + 1 – 2, 3λ – 4 – 3 i.e. 5λ – 3, 2λ – 1, 3λ – 7
Since, PM is perpendicular to the line whose direcction ratios are 5, 2, 3,
5(5λ – 3) + 2(2λ – 1) + 3(3λ – 7) = 0
25λ – 15 + 4λ – 2 + 9λ – 21 =0
38λ – 38 = 0 ∴ λ = 1
Substituting λ = 1 in (1), we get.
M = (5 – 3, 2 + 1, 3 – 4) = (2, 3, -1).
Hence, the coordinates of the foot of perpendicular are (2, 3, – 1).
Question 16.
By computing the shortest distance determine whether following lines intersect each other.
Solution:
The shortest distance between the lines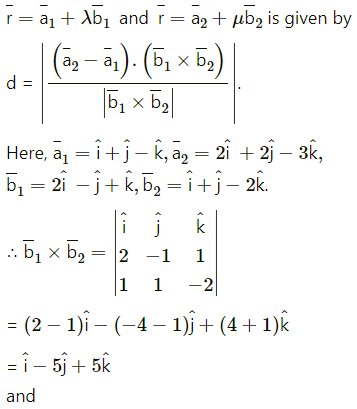
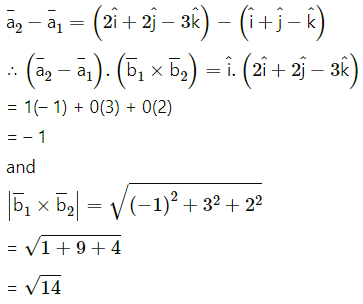
Shortest distance between the lines is 0.
∴ the lines intersect each other.
Solution:
The shortest distance between the lines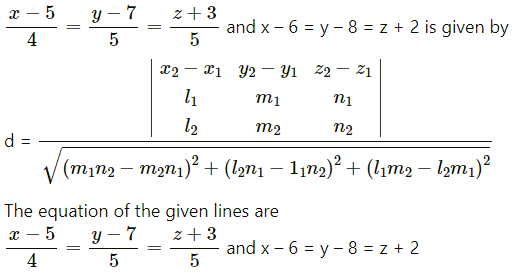
∴ x1 = 5, y1 = 7, z1 = 3, x2 = 6, y2 = 8, z2 = 2,
l1 = 4, m1 = 5, n1 = 1, l2 = 1, m2 = -2, n2 = 1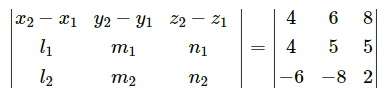
= 4(-6 + 2) – 6(7 – 1) + 8(-14 + 6)
= -16 – 36 – 64
= -116
and
(m1n2 – m2n1)2 + (l2n1 – l1n2)2 + (l1m2 – l2m1)2
= (-6 + 2)2 + (1 – 7)2 + (1 – 7)2 + (-14 + 6)2
= 16 + 36 + 64
= 116
Hence, the required shortest distance between the given lines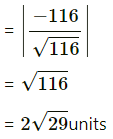
or
Shortest distance between the lines is 0.
∴ the lines intersect each other.
Question 17.
Solution:
Here, (x1, y1, z1) ≡ (1, -1, 1),
(x2, y2, z2) ≡ (2, -m, 2),
a1 = 2, b1 = 3, c1 = 4,
a2 = 1, b2 = 2, c2 = 1
Substituting these values in (1), we get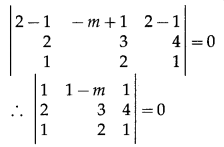
∴ 1(3 – 8) – (1 – m)(2 – 4) + 1 (4 – 3) = 0
∴ -5 + 2 – 2m + 1 = 0
∴ -2m = 2
∴ m = -1.
Question 18.
Find the vector and Cartesian equations of the line passing through the point (-1, -1, 2) and parallel to the line 2x – 2 = 3y + 1 = 6z – 2.
Solution:
Let a¯ be the position vector of the point A (-1, -1, 2) w.r.t. the origin.![]()
The equation of given line is
x – 2 = 3y + 1 = 6z – 2.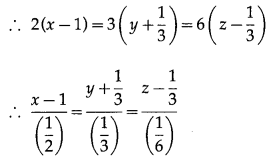
The direction ratios of this line are
Question 19.
Solution:
Question 20.
Solution:
Let the required line have direction ratios a, b, c
Since the line passes through the origin, its cartesian equations are![]()
This line is perpendicular to the line
x – 1 = y – 2 = z – 1 whose direction ratios are 1, 1, 1.
∴ 1(4b – 3c) + 1(4a – 2c) + 1(3a – 2b) = 0
∴ 4b – 3c + 4a – 2c + 3a – 2b = 0
∴ 7a + 2b – 5c = 0
From (2) and (3), we get
Question 21.
Write the vector equation of the line whose Cartesian equations are y = 2 and 4x – 3z + 5 = 0.
Solution:
4x – 3z + 5 = 0 can be written as

Question 22.
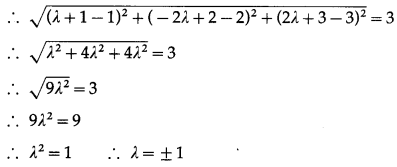
When λ = 1, M = (1 + 1, -2 + 2, 2 + 3) … [By (1)]
i. e. M = (2, 0, 5)
When λ = -1, M = (1 – 1, 2 + 2, -2 + 3) … [By (1)]
i. e. M = (0, 4, 1)
Hence, the coordinates of the required points are (2, 0, 5) and (0, 4, 1).
