Chapter 6 Trigonometry Set 6

Question 1.
Choose the correct alternative answer for the following questions.

i. sin θ.cosec θ = ?

Answer:
(A)

ii. cosec 45° = ?

Answer:
(B)

iii. 1 + tan² θ = ?
(A) cot² θ
(B) cosec² θ
(C) sec² θ
(D) tan² θ
Answer:
(C)

iv. When we see at a higher level, from the horizontal line, angle formed is ______
(A) angle of elevation.
(B) angle of depression.
(C) 0
(D) straight angle.
Answer:
(A)

Question 2.
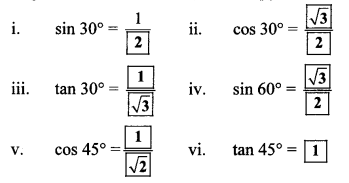
If sin θ = 11/61, find the value of cos θ using trigonometric identity.
Solution:
sin θ =  … [Given]
We know that,
sin² θ + cos² θ = 1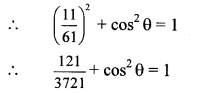


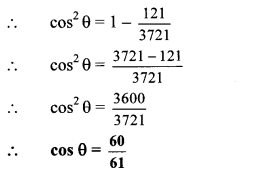
…[Taking square root of both sides]

Question 3.
If tan θ = 2, find the values of other trigonometric ratios.
Solution:
tan θ = 2 …[Given]
We know that,
1 + tan² θ = sec⁷ θ
∴ 1 + (2)⁷ = sec⁷ θ
∴ 1 + 4 = sec⁷ θ
∴ sec⁷ θ = 5
∴ sec θ = √5 …[Taking square root of both sides]

Question 4.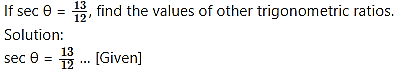

We know that,
1 + tan² θ = sec² θ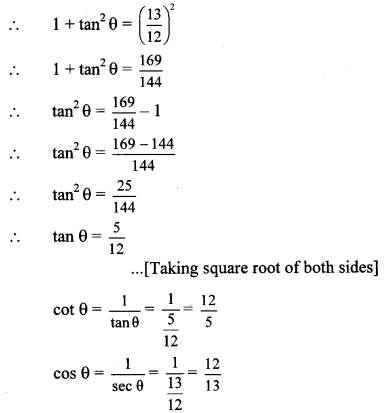

Question 5.
Prove the following:
i. sec θ (1 – sin θ) (sec θ + tan θ) = 1
ii. (sec θ + tan θ) (1 – sin θ) = cos θ
iii. sec² θ + cosec² θ = sec² θ × cosec² θ
iv. cot² θ – tan² θ = cosec² θ – sec² θ
v. tan⁴ θ + tan² θ = sec⁴ θ – sec² θ

vii. sec⁶ x – tan⁶ x = 1 + 3 sec² x × tan² x

Proof:
i. L.H.S. = sec θ (1 – sin θ) (sec θ + tan θ)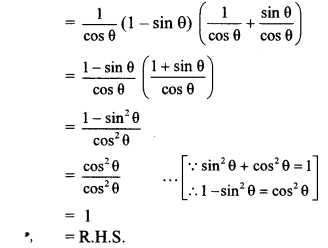

∴ sec θ (1 – sin θ) (sec θ + tan θ) = 1

ii. L.H.S. = (sec θ + tan θ) (1 – sin θ)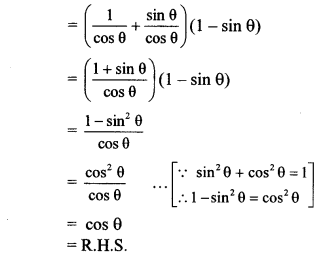

∴ (sec θ + tan θ) (1 – sin θ) = cos θ

iii. L.H.S. = sec² θ + cosec² θ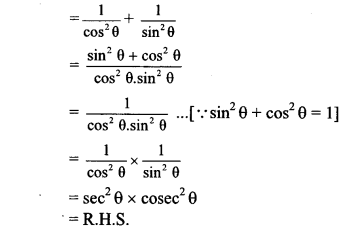

∴ sec² θ + cosec² θ = sec² θ × cosec² θ

iv. L.H.S. = cot² θ – tan² θ
= (cosec² θ – 1) – (sec² θ – 1)
[∵ tan² θ = sec² θ – 1,
cot² θ = cosec² θ – 1]
= cosec² θ – 1 – sec² θ + 1
cosec² θ – sec² θ
= R.H.S.
∴ cot² θ – tan² θ = cosec² θ – sec² θ

v. L.H.S. = tan⁴ θ + tan² θ
= tan² θ (tan² θ + 1)
= tan² θ. sec² θ
…[∵ 1 + tan² θ = sec² θ]
= (sec² θ – 1) sec² θ
…[∵ tan² θ = sec² θ – 1]
= sec⁴ θ – sec² θ
= R.H.S.
∴ tan⁴ θ + tan² θ = sec⁴ θ – sec² θ

vii. L.H.S. = sec⁶ x – tan⁶ x
= (sec² x)³ – tan⁶ x
= (1 + tan² x)³ – tan⁶ x …[∵ 1 + tan² θ = sec² θ]
= 1 + 3tan² x + 3(tan² x)² + (tan² x)³ – tan⁶ x …[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= 1 + 3 tan² x (1 + tan² x) + tan⁶ x – tan⁶ x
= 1 + 3 tan² x sec² x …[∵ 1 + tan² θ = sec² θ]
= R.H.S.
∴ sec³x – tan⁶x = 1 + 3sec²x.tan²x


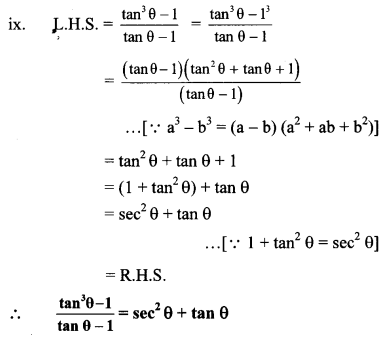
x. We know that,
sin² θ + cos² θ = 1
∴ 1 – sin² θ = cos² θ
∴ (1 – sin θ) (1 + sin θ) = cos θ. cos θ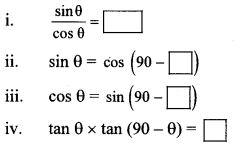

Question 6.
A boy standing at a distance of 48 metres from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
Solution:
Let AB represent the height of the building and point C represent the position of the boy.
Angle of elevation = ∠ACB = 30°
BC = 48 m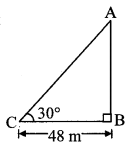

In right angled ∆ABC,
tan 30° = ABBC … [By definition]

∴ The height of the building is 16√3 m.

Question 7.
From the top of the lighthouse, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the lighthouse is 100 metres, then find how far the ship is from the lighthouse.
Solution:
Let AB represent the height of lighthouse and point C represent the position of the ship.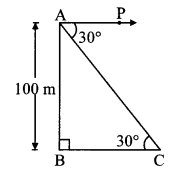

Angle of depression ∠PAC 30°
AB = 100m.
Now, ray AP || seg BC
∴ ∠ACB = ∠PAC … [Alternate angles]
∴ ∠ACB = 30°
AB = 100m

Question 8.
Two buildings are in front of each other on a road of width 15 metres. From the top of the first building, having a height of 12 metre, the angle of elevation of the top of the second building is 30°. What is the height of the second building?
Solution:
Let AB and CD represent the heights of the two buildings, and BD represent the width of the road.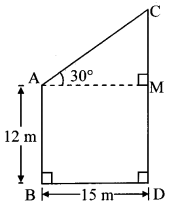

Draw seg AM ⊥ seg CD
Angle of elevation = ∠CAM = 30°
AB = 12m
BD = 15m
In ꠸ ABDM,
∠B = ∠D = 90°
∠M 90° …[segAM ⊥ segCD]
∠A 90° …[Remaining angle of ꠸ABDM]
꠸ABDM is a rectangle …[Each angle is 90°]

∴ The height of the second building is 20.65 m.

Question 9.
A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20 m. If the platform is 2 m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
Solution:
Let AB represent the length of the ladder and AE represent the height of the platform.

Draw seg AC ⊥ seg BD.
Angle of elevation = ∠BAC = 70°
AB = 20 m
AE = 2m
In right angled ∆ABC,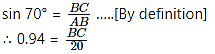

∴ BC = 0.94 × 20
= 18.80 m
In ꠸ACDE,
∠E = ∠D = 90°
∠C = 90° … [seg AC ⊥ seg BD]
∴ ∠A = 90° … [Remaining angle of ꠸ACDE]
∴ ꠸ACDE is a rectangle. … [Each angle is 90°]
∴ CD = AE = 2 m … [Opposite sides of a rectangle]
Now, BD = BC + CD … [B – C – D]
= 18.80 + 2
= 20.80 m
∴ The maximum height from the ground upto which the ladder can reach is 20.80 metres.

Question 10.
While landing at an airport, a pilot made an angle of depression of 20°. Average speed of the plane was 200 km/hr. The plane reached the ground after 54 seconds. Find the height at which the plane was when it started landing, (sin 20° = 0.342)
Solution:
Let AC represent the initial height and point A represent the initial position of the plane.
Let point B represent the position where plane lands.
Angle of depression = ∠EAB = 20°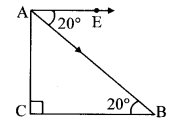

Now, seg AE || seg BC
∴ ∠ABC = ∠EAB … [Alternate angles]
∴ ∠ABC = 20°

∴ AC = 0.342 × 3000
= 1026 m
∴ The plane was at a height of 1026 m when it started landing.