I. Select the correct option from the given alternatives.
Question 1.
Question 2.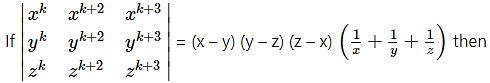
(a) k = -3
(b) k = -1
(c) k = 1
(d) k = 3
Answer:
(b) k = -1
Hint:
Question 3.
Answer:
(b) D is independent of φ
Question 4.
The value of a for which the system of equations x + (a + 1)y + (a + 2 z = 0, ax + (a + 1)y + (a + 2)z = 0 and x + y + z = 0 has a non zero solution is
(a) 0
(b) -1
(c) 1
(d) 2
Answer:
(b) -1
Hint:
The given system of equations will have a non-zero solution, if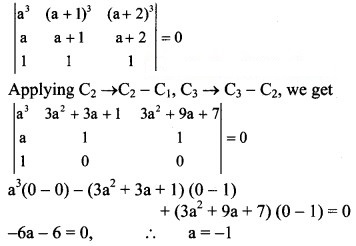
Question 5.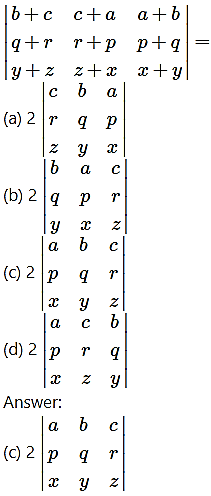
Hint:
Question 6.
The system 3x – y + 4z = 3, x + 2y – 3z = -2 and 6x + 5y + λz = -3 has atleast one solution when
(a) λ = -5
(b) λ = 5
(c) λ = 3
(d) λ = -13
Answer:
(a) λ = -5
Hint:
The given system of equations will have more than one solution if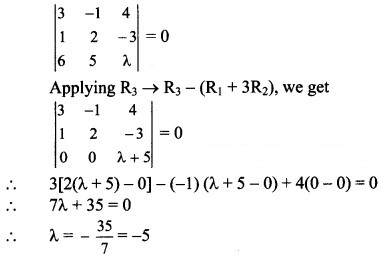
Question 7.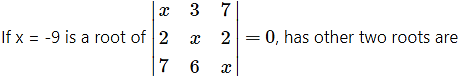
(a) 2, -7
(b) -2, 7
(c) 2, 7
(d) -2, -7
Answer:
(c) 2, 7
Hint:
Question 8.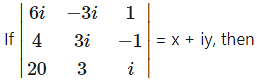
(a) x = 3, y = 1
(b) x = 1, y = 3
(c) x = 0, y = 3
(d) x = 0, y = 0
Answer:
(d) x = 0, y = 0
Question 9.
If A(0, 0), B(1, 3) and C(k, 0) are vertices of triangle ABC whose area is 3 sq. units, then the value of k is
(a) 2
(b) -3
(c) 3 or -3
(d) -2 or 2
Answer:
(d) -2 or 2
Question 10.
Which of the following is correct?
(a) Determinant is a square matrix
(b) Determinant is number associated to matrix
(c) Determinant is a number associated with a square matrix
(d) None of these
Answer:
(c) Determinant is a number associated with a square matrix
II. Answer the following questions.
Question 1.
Evaluate:
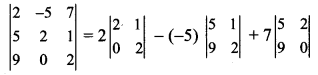
= 2(4 – 0) + 5(10 – 9) + 7(0 – 18)
= 2(4) + 5(1) + 7(-18)
= 8 + 5 – 126
= -113

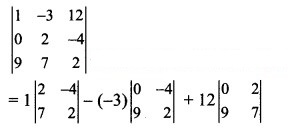
= 1(4 + 28) + 3(0 + 36) + 12(0 – 18)
= 1(32) + 3(36) + 12(-18)
= 32 + 108 – 216
= -76
Question 2.
Solution:
Question 3.
Evaluate:
by using properties.
Solution:
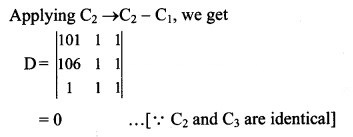
Question 4.
Find the minors and cofactors of elements of the determinants.
Solution: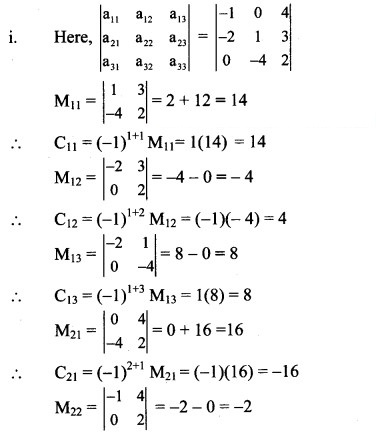

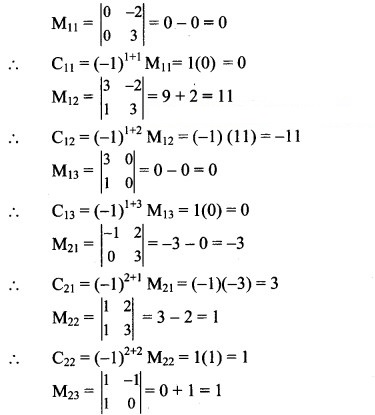
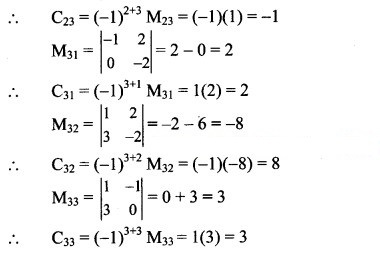
Question 5.
Find the values of x, if
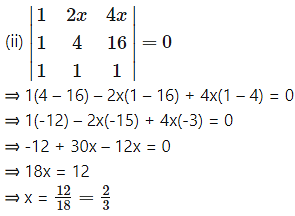
Question 6.
Solution:
Question 7.
Without expanding the determinants, show that
Solution: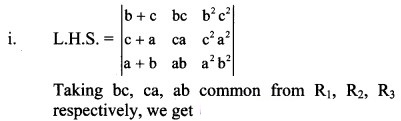


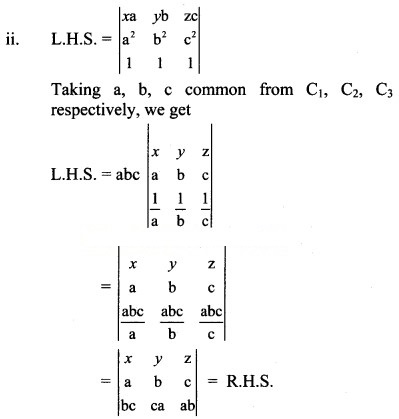


Question 8.
Solution: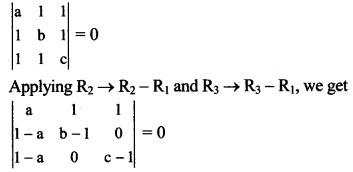

Question 9.
Solve the following linear equations by Cramer’s Rule.
(i) 2x – y + z = 1, x + 2y + 3z = 8, 3x + y – 4z = 1
(iii) 2x + 3y + 3z = 5, x – 2y + z = -4, 3x – y – 2z = 3
(iv) x + y + 2z = 7, 3x + 4y – 5z = 5, 2x – y + 3z = 12
Solution:
(i) Given equations are
2x – y + z = 1
x + 2y + 3z = 8
3x + y – 4z = 1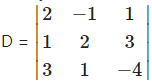
= 2(-8 – 3) – (-1)(-4 – 9) + 1(1 – 6)
= 2(-11) + 1(-13) + 1(-5)
= -22 – 13 – 5
= -40 ≠ 0
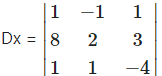
= 1(-8 – 3) – (-1)(-32 – 3) + 1(8 – 2)
= 1(-11) + 1(-35) + 1(6)
= -11 – 35 + 6
= -40

= 2(-32 – 3) -1(-4 – 9) + 1(1 – 24)
= 2(-35) – 1(-13) + 1(-23)
= -70 + 13 – 23
= -80
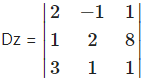
= 2(2 – 8) – (-1)(1 – 24) + 1(1 – 6)
= 2(-6) + 1(-23) + 1(-5)
= -12 – 23 – 5
= -40
By Cramer’s Rule,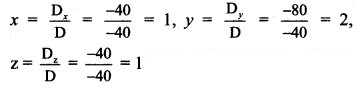
∴ x = 1, y = 2 and z = 1 are the solutions of the given equations.

= 2(18 – 0) -2(0 – 18) + 0
= 2(18) – 2(-18)
= 36 + 36
= 72 ≠ 0
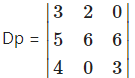
= 3(18 – 0) – 2(15 – 24) + 0
= 3(18) – 2(-9)
= 54 + 18
= 72
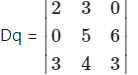
= 2(15 – 24) – 3(0 – 18) + 0
= 2(-9) – 3(-18)
= -18 + 54
= 36
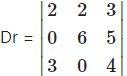
= 2(24 – 0) – 2(0 – 15) + 3(0 – 18)
= 2(24) – 2(-15) + 3(-18)
= 48 + 30 – 54
= 24
By Cramer’s Rule,
∴ x = 1, y = 2 and z = 3 are the solutions of the given equations.
(iii) Given equations are
2x + 3y + 3z = 5
x – 2y + z = -4
3x – y – 2z = 3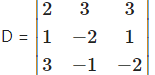
= 2(4 + 1) – 3(-2 – 3) + 3(-1 + 6)
= 2(5) – 3(-5) + 3(5)
= 10 + 15 + 15
= 40 ≠ 0
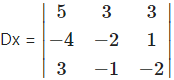
= 5(4 + 1) – 3(8 – 3) + 3(4 + 6)
= 5(5) – 3(5) + 3(10)
= 25 – 15 + 30
= 40
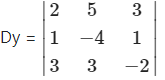
= 2(8 – 3) – 5(-2 – 3) + 3(3 + 12)
= 2(5) – 5(-5) + 3(15)
= 10 + 25 + 45
= 80

= 2(-6 – 4) – 3(3 + 12) + 5(-1 + 6)
= 2(-10) – 3(15) + 5(5)
= -20 -45 + 25
= -40
By Cramer’s Rule,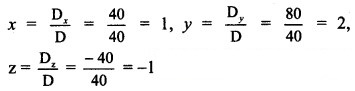
∴ x = 1, y = 2 and z = -1 are the solutions of the given equations.
(iv) Given equations are
x – y + 2z = 7
3x + 4y – 5z = 5
2x – y + 3z = 12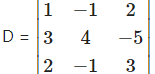
= 1(12 – 5) – (-1)(9 + 10) + 2(-3 – 8)
= 1(7) + 1(19) + 2(-11)
= 7 + 19 – 22
= 4 ≠ 0
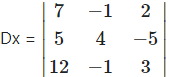
= 7(12 – 5) – (-1)(15 + 60) + 2(-5 – 48)
= 7(7) + 1(75) + 2(-53)
= 49 + 75 – 106
= 18

= 1(15 + 60) – 7(9 + 10) + 2(36 – 10)
= 1(75) – 7(19) + 2(26)
= 75 – 133 + 52
= -6
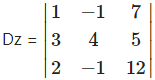
= 1(48 + 5) – (-1)(36 – 10) + 7(-3 – 8)
= 1(53) + 1(26) + 7(-11)
= 53 + 26 – 77
= 2
By Cramer’s Rule,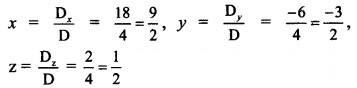
![]()
Question 10.
Find the value of k, if the following equations are consistent.
(i) (k + 1)x + (k – 1)y + (k – 1) = 0
(k – 1)x + (k + 1)y + (k – 1) = 0
(k – 1)x + (k – 1)y + (k + 1) = 0
(ii) 3x + y – 2 = 0, kx + 2y – 3 = 0 and 2x – y = 3
(iii) (k – 2)x + (k – 1)y = 17, (k – 1)x +(k – 2)y = 18 and x + y = 5
Solution:
(i) Given equations are
(k + 1)x + (k – 1)y + (k – 1) = 0
(k – 1)x + (k + 1)y + (k – 1) = 0
(k – 1)x + (k – 1)y + (k + 1) = 0
Since these equations are consistent,
⇒ 2(2k + 2 + 2k – 2) – 0 + (k – 1) (4 – 0) = 0
⇒ 2(4k) + (k – 1)4 = 0
⇒ 8k + 4k – 4 = 0
⇒ 12k – 4 = 0![]()
(ii) Given equations are
3x + y – 2 = 0
kx + 2y – 3 = 0
2x – y = 3, i.e., 2x – y – 3 = 0.
Since these equations are consistent,
⇒ 3(-6 – 3) – 1(-3k + 6) – 2(-k – 4) = 0
⇒ 3(-9) – 1(-3k + 6) – 2(-k – 4) = 0
⇒ -27 + 3k – 6 + 2k + 8 = 0
⇒ 5k – 25 = 0
⇒ k = 5
(iii) Given equations are
(k – 2)x + (k – 1)y = 17
⇒ (k – 2)x + (k – 1)y – 17 = 0
(k – 1)x + (k – 2)y = 18
⇒ (k – 1)x + (k – 2)y – 18 = 0
x + y = 5
⇒ x + y – 5 = 0
Since these equations are consistent,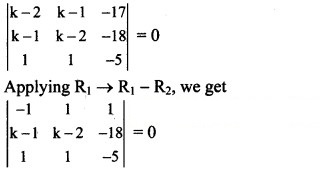
⇒ -1(-5k + 10 + 18) – 1(-5k + 5 + 18) + 1(k – 1 – k + 2) = 0
⇒ -1(-5k + 28) – 1(-5k + 23) + 1(1) = 0
⇒ 5k – 28 + 5k – 23 + 1 = 0
⇒ 10k – 50 = 0
⇒ k = 5
Question 11.
Find the area of triangle whose vertices are
(i) A(-1, 2), B(2, 4), C(0, 0)
(ii) P(3, 6), Q(-1, 3), R(2, -1)
(iii) L(1, 1), M(-2, 2), N(5, 4)
Solution:
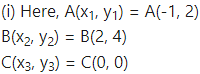
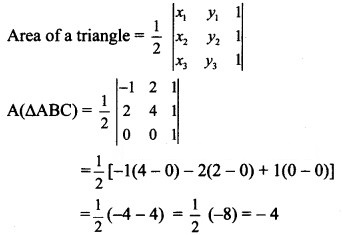
Since area cannot be negative,
A(ΔABC) = 4 sq. units
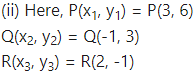

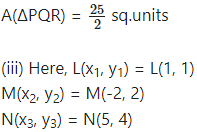

Since area cannot be negative,
A(ΔLMN) =13/2 sq. units
Question 12.
Find the value of k,
(i) if the area of a triangle is 4 square units and vertices are P(k, 0), Q(4, 0), R(0, 2).
(ii) if area of triangle is 33/2 square units and vertices are L(3, -5), M(-2, k), N(1, 4).
Solution: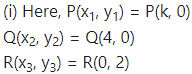
A(ΔPQR) = 4 sq. units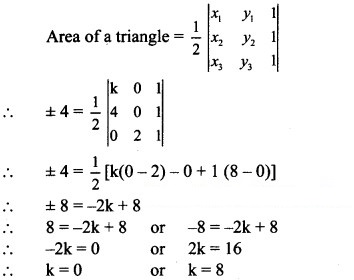
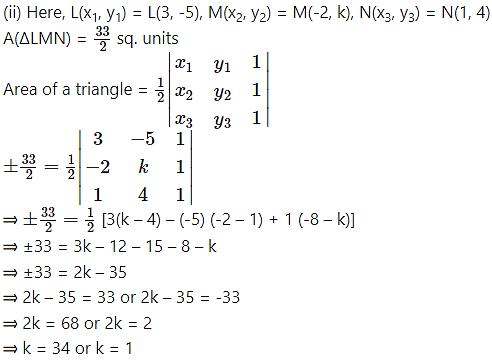
Question 13.
Find the area of quadrilateral whose vertices are A(0, -4), B(4, 0), C(-4,0), D (0, 4).
Solution:
A(0, -4), B(4, 0), C(-4, 0), D(0, 4)

∴ A(ABDC) = A(ΔABC) + A(ΔBDC)
= 16 + 16
= 32 sq.units
Question 14.
An amount of ₹ 5000 is put into three investments at the rate of interest of 6%, 7%, and 8% per annum respectively. The total annual income is ₹ 350. If the combined income from the first two investments is ₹ 70 more than the income from the third, find the amount of each investment.
Solution:
Let the amount of each investment be ₹ x, ₹ y and ₹ z.
According to the given conditions,
x + y + z = 5000,
6% x + 7% y + 8% z = 350



∴ The amounts of investments are ₹ 1750, ₹ 1500, and ₹ 1750.
Question 15.
Show that the lines x – y = 6, 4x – 3y = 20 and 6x + 5y + 8 = 0 are concurrent. Also, find the point of concurrence.
Solution:
Given equations of the lines are
x – y = 6, i.e., x – y – 6 = 0 ……(i)
4x – 3y = 20, i.e., 4x – 3y – 20 = 0 …..(ii)
6x + 5y + 8 = 0 ……(iii)
The given lines will be concurrent, if
= 1(-24 + 100) – (-1) (32 + 120) – 6(20 + 18)
= 1(76) + 1(152) – 6(38)
= 76 + 152 – 228
= 0
∴ The given lines are concurrent.
To find the point of concurrence, solve any two equations.
Multiplying (i) by 5, we get
5x – 5y – 30 = 0 …….(iv)
Adding (iii) and (iv), we get
11x – 22 = 0
∴ x = 2
Substituting x = 2 in (i), we get
2 – y – 6 = 0
∴ y = -4
∴ The point of concurrence is (2, -4).
Question 16.
Show that the following points are collinear using determinants:
(i) L(2, 5), M(5, 7), N(8, 9)
(ii) P(5,1), Q(1, -1), R(11, 4)
Solution:
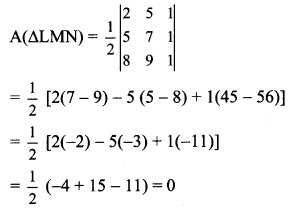
∴ The points L, M, N are collinear.
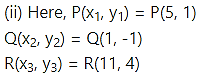
If A(ΔPQR) = 0, then the points P, Q, R are collinear.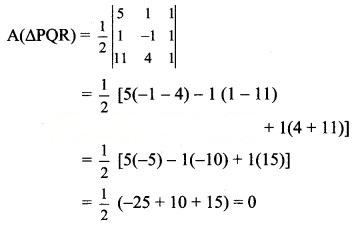
∴ The points P, Q, R are collinear.
