Maharashtra Board Class 11 Maths Part 2 Chapter 6 Functions Ex 6.1 Solution

Question 1.
Check if the following relations are functions.
(a)

Solution:
Yes.
Reason: Every element of set A has been assigned a unique element in set B.

(b)

Solution:
No.
Reason: An element of set A has been assigned more than one element from set B.

(c)

Solution:
No.
Reason:
Not every element of set A has been assigned an image from set B.

Question 2.
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {-1, 0, 1, 2, 3}? Justify.
(i) {(1, 0), (3, 3), (2, -1), (4, 1), (2, 2)}
(ii) {(1, 2), (2, -1), (3, 1), (4, 3)}
(iii) {(1, 3), (4, 1), (2, 2)}
(iv) {(1, 1), (2, 1), (3, 1), (4, 1)}
Solution:
(i) {(1, 0), (3, 3), (2, -1), (4, 1), (2, 2)} does not represent a function.
Reason: (2, -1), (2, 2), show that element 2 ∈ A has been assigned two images -1 and 2 from set B.

(ii) {(1, 2), (2, -1), (3, 1), (4, 3)} represents a function.
Reason: Every element of set A has been assigned a unique image in set B.

(iii) {(1, 3), (4, 1), (2, 2)} does not represent a function.
Reason:
3 ∈ A does not have an image in set B.

(iv) {(1, 1), (2, 1), (3, 1), (4, 1)} represents a function
Reason: Every element of set A has been assigned a unique image in set B.

Question 3.
Check if the relation given by the equation represents y as function of x.

(iii) x² – y = 25
∴ y = x² – 25
∴ For every value of x, there is a unique value of y.
∴ y is a function of x.

(iv) 2y + 10 = 0
∴ y = -5
∴ For every value of x, there is a unique value of y.
∴ y is a function of x.

(v) 3x – 6 = 21
∴ x = 9
∴ x = 9 represents a point on the X-axis.
There is no y involved in the equation.
So the given equation does not represent a function.

Question 4.

Question 5.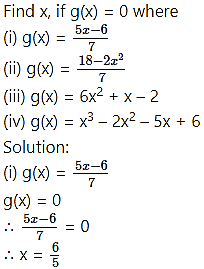

(iv) g(x) = x³ – 2x² – 5x + 6
= ( x- 1) (x² – x – 6)
= (x – 1) (x + 2) (x – 3)
g(x) = 0
∴ (x – 1) (x + 2) (x – 3) = 0
∴ x – 1 = 0 or x + 2 = 0 or x – 3 = 0
∴ x = 1, -2, 3

Question 6.

Question 7.

Question 8.
Find the domain and range of the following functions.
(i) f(x) = 7x² + 4x – 1
Solution:
f(x) = 7x² + 4x – 1
f is defined for all x.
∴ Domain of f = R (i.e., the set of real numbers)

f(x) ≥ 0 … [∵ The value of square root function is non-negative]
∴ Range of f = [0, ∞)

∴ -4 ≤ x ≤ 4
∴ Domain of f = [-4, 4]
Clearly, f(x) ≥ 0 and the value of f(x) would be maximum when the quantity subtracted from 16 is minimum i.e. x = 0
∴ Maximum value of f(x) = √16 = 4
∴ Range of f = [0, 4]

Question 9.
Express the area A of a square as a function of its
(a) side s
(b) perimeter P
Solution:

Question 10.
Express the area A of a circle as a function of its
(i) radius r
(ii) diameter d
(iii) circumference C
Solution:
(i) Area (A) = πr²

Question 11.
An open box is made from a square of cardboard of 30 cms side, by cutting squares of length x centimeters from each corner and folding the sides up. Express the volume of the box as a function of x. Also, find its domain.
Solution:

Length of the box = 30 – 2x
Breadth of the box = 30 – 2x
Height of the box = x
Volume = (30 – 2x)² x, x < 15, x ≠ 15, x > 0
= 4x(15 – x)², x ≠ 15, x > 0
Domain (0, 15)

Question 12.
Let f be a subset of Z × Z defined by f = {(ab, a + b): a, b ∈ Z}. Is f a function from Z to Z? Justify?
Solution:
f = {(ab, a + b): a, b ∈ Z}
Let a = 1, b = 1. Then, ab = 1, a + b = 2
∴ (1, 2) ∈ f
Let a = -1, b = -1. Then, ab = 1, a + b = -2
∴ (1, -2) ∈ f
Since (1, 2) ∈ f and (1, -2) ∈ f,
f is not a function as element 1 does not have a unique image.

Question 13.
Check the injectivity and surjectivity of the following functions.
(i) f : N → N given by f(x) = x²
Solution:
f: N → N given by f(x) = x²

∴ f is injective.
For every y = x² ∈ N, there does not exist x ∈ N.
Example: 7 ∈ N (codomain) for which there is no x in domain N such that x² = 7
∴ f is not surjective.

(ii) f : Z → Z given by f(x) = x²
Solution:
f: Z → Z given by f(x) = x2

∴ f is not injective.
(Example: f(-2) = 4 = f(2). So, -2, 2 have the same image. So, f is not injective.)
Since x² ≥ 0,
f(x) ≥ 0
Therefore all negative integers of codomain are not images under f.
∴ f is not surjective.

(iii) f : R → R given by f(x) = x²
Solution:
f : R → R given by f(x) = x²

∴ f is not injective.
f(x) = x² ≥ 0
Therefore all negative integers of codomain are not images under f.
∴ f is not surjective.

(iv) f : N → N given by f(x) = x³
Solution:
f: N → N given by f(x) = x³

∴ f is injective.
Numbers from codomain which are not cubes of natural numbers are not images under f.
∴ f is not surjective.

(v) f : R → R given by f(x) = x³
Solution:
f: R → R given by f(x) = x³

∴ For every y ∈ R, there is some x ∈ R.
∴ f is surjective.

Question 14.
Show that if f : A → B and g : B → C are one-one, then gof is also one-one.
Solution:

Question 15.
Show that if f : A → B and g : B → C are onto, then gof is also onto.
Solution:
Since g is surjective (onto),
there exists y ∈ B for every z ∈ C such that
g(y) = z …….(i)
Since f is surjective,
there exists x ∈ A for every y ∈ B such that
f(x) = y …….(ii)
(gof) x = g(f(x))
= g(y) ……[From (ii)]
= z …..[From(i)]
i.e., for every z ∈ C, there is x in A such that (gof) x = z
∴ gof is surjective (onto).

Question 16.

Question 17.
Express the following exponential equations in logarithmic form:

Solution:

Question 18.
Express the following logarithmic equations in exponential form:

Question 19.
Find the domain of
(i) f(x) = ln (x – 5)
(ii) f(x) = log10 (x² – 5x + 6)
Solution:
(i) f(x) = ln (x – 5)
f is defined, when x – 5 > 0
∴ x > 5
∴ Domain of f = (5, ∞)

(ii) f(x) = log₁₀ (x² – 5x + 6)
x² – 5x + 6 = (x – 2) (x – 3)
f is defined, when (x – 2) (x – 3) > 0
∴ x < 2 or x > 3
Solution of (x – a) (x – b) > 0 is x < a or x > b where a < b
∴ Domain of f = (-∞, 2) ∪ (3, ∞)

Question 20.
Write the following expressions as sum or difference of logarithms:

Solution:

Solution:

Solution:

Solution:

Question 21.
Write the following expressions as a single logarithm.
(i) 5 log x + 7 log y – log z
Solution:

Solution:

(iii) ln (x + 2) + ln (x – 2) – 3 ln (x + 5)
Solution:

Question 22.
Given that log 2 = a and log 3 = b, write log √96 terms of a and b.
Solution:

Question 23.
Prove that:

Solution:

Solution:

Question 24.

Question 25.
Solve for x:
(i) log 2 + log (x + 3) – log (3x – 5) = log 3
Solution:

Check:
If x = 3 satisfies the given condition, then our answer is correct.
L.H.S. = log 2 + log (x + 3) – log (3x – 5)
= log 2 + log (3 + 3) – log (9 – 5)
= log 2 + log 6 – log 4
= log (2 × 6) – log 4
= log 12/4
= log 3
= R.H.S.
Thus, our answer is correct.

Solution:


∴ x² = 10x + 11
∴ x² – 10x – 11 = 0
∴ (x – 11)(x + 1) = 0
∴ x = 11 or x = -1
But log of a negative numbers does not exist
∴ x ≠ -1
∴ x = 11

Solution:

Solution:

∴ a + a² = 6
∴ a² + a – 6 = 0
∴ (a + 3)(a – 2) = 0
∴ a + 3 = 0 or a – 2 = 0
∴ a = -3 or a = 2
Since 2x = -3 is not possible,
2x = 2 = 21
∴ x = 1

Question 26.

Solution:

Question 27.

Solution:

Question 28.

Solution: