(I) Select the appropriate option from the given alternatives.
Question 1.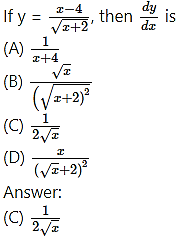
Hint:
Question 2.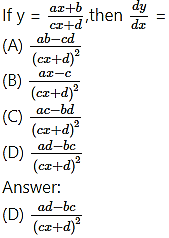
Hint: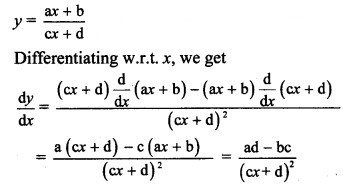
Question 3.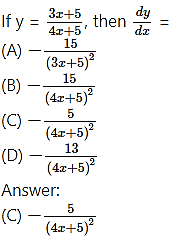
Hint: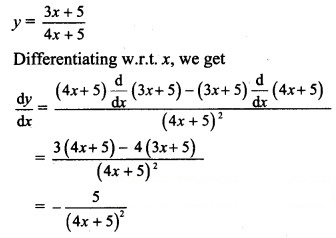
Question 4.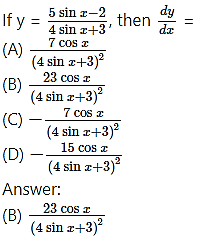
Hint:
Question 5.
Suppose f(x) is the derivative of g(x) and g(x) is the derivative of h(x).
If h(x) = a sin x + b cos x + c, then f(x) + h(x) =
(A) 0
(B) c
(C) -c
(D) -2(a sin x + b cos x)
Answer:
(B) c
Hint:
h(x) = a sin x + b cos x + c
Differentiating w.r.t. x, we get
h'(x) = a cos x – b sin x = g(x) …..[given]
Differentiating w.r.t. x, we get
g'(x) = -a sin x – b cos x = f(x) …..[given]
∴ f(x) + h(x) = -a sin x – b cos x + a sin x + b cos x + c
∴ f(x) + h(x) = c
Question 6.
If f(x) = 2x + 6, for 0 ≤ x ≤ 2
= ax2 + bx, for 2 < x ≤ 4
is differentiable at x = 2, then the values of a and b are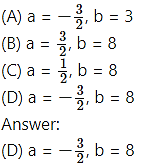
Hint:
f(x) = 2x + 6, 0 ≤ x ≤ 2
= ax2 + bx, 2 < x ≤ 4
Lf'(2) = 2, Rf'(2) = 4a + b
Since f is differentiable at x = 2,
Lf'(2) = Rf'(2)
∴ 2 = 4a + b …..(i)
f is continuous at x = 2.![]()
∴ 4a + 2b = 2(2) + 6
∴ 4a + 2b = 10
∴ 2a + b = 5 …..(ii)
Solving (i) and (ii), we get![]()
Question 7.
If f(x) = x2 + sin x + 1, for x ≤ 0
= x2 – 2x + 1, for x ≤ 0, then
(A) f is continuous at x = 0, but not differentiable at x = 0
(B) f is neither continuous nor differentiable at x = 0
(C) f is not continuous at x = 0, but differentiable at x = 0
(D) f is both continuous and differentiable at x = 0
Answer:
(A) f is continuous at x = 0, but not differentiable at x = 0
Hint:
Question 8.
(A) 48
(B) 49
(C) 50
(D) 51
Answer:
(C) 50
Hint: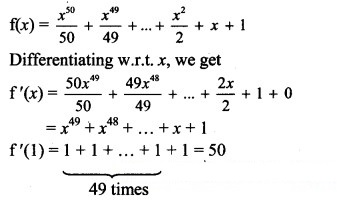
(II).
Question 1.
Determine whether the following function is differentiable at x = 3 where,
f(x) = x2 + 2, for x ≥ 3
= 6x – 7, for x < 3.
Solution:
f(x) = x2 + 2, x ≥ 3
= 6x – 7, x < 3
Differentiability at x = 3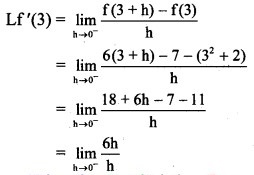
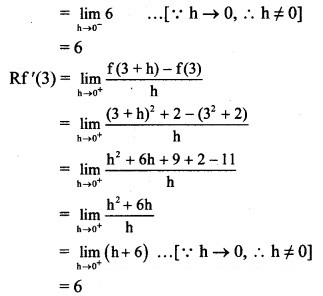
Here, Lf'(3) = Rf'(3)
∴ f is differentiable at x = 3.
Question 2.
Find the values of p and q that make function f(x) differentiable everywhere on R.
f(x) = 3 – x, for x < 1
= px2 + qx, for x ≥ 1.
Solution:
f(x) is differentiable everywhere on R.
∴ f(x) is differentiable at x = 1.
∴ f(x) is continuous at x = 1.
f(x) is differentiable at x = 1.
∴ Lf'(1) = Rf'(1)
∴ -1 = 2p + q …..(ii)
Subtracting (i) from (ii), we get
p = -3
Substituting p = -3 in (i), we get
p + q = 2
∴ -3 + q = 2
∴ q = 5
Question 3.
Determine the values of p and q that make the function f(x) differentiable on R where
f(x) = px3, for x < 2
= x2 + q, for x ≥ 2
Solution:
f(x) is differentiable on R.
∴ f(x) is differentiable at x = 2.
∴ f(x) is continuous at x = 2.
Continuity at x = 2:
f(x) is continuous at x = 2.
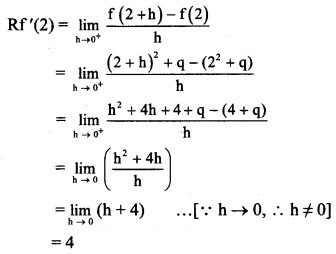
f(x) is differentiable at x = 2.
∴ Lf'(2) = Rf'(2)
∴ 12p = 4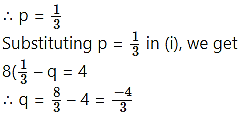
Question 4.
Determine all real values of p and q that ensure the function
f(x) = px + q, for x ≤ 1
is differentiable at x = 1.
Solution:
f(x) is differentiable at x = 1.
∴ f(x) is continuous at x = 1.
Continuity at x= 1:
f(x) is continuous at x = 1.

Question 5.
Discuss whether the function f(x) = |x + 1| + |x – 1| is differentiable ∀ x ∈ R.
Solution:
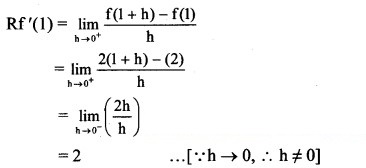
Here, Lf'(1) ≠ Rf'(1)
∴ f is not differentiable at x = 1.
∴ f is not differentiable at x = -1 and x = 1.
∴ f is not differentiable ∀ x ∈ R.
Question 6.
Test whether the function
f(x) = 2x – 3, for x ≥ 2
= x – 1, for x < 2
is differentiable at x = 2.
Solution:
Question 7.
Test whether the function
f(x) = x2 + 1, for x ≥ 2
= 2x + 1, for x < 2
is differentiable at x = 2.
Solution: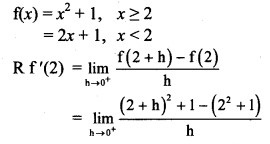

Question 8.
Test whether the function
f(x) = 5x – 3x2, for x ≥ 1
= 3 – x, for x < 1
is differentiable at x = 1.
Solution: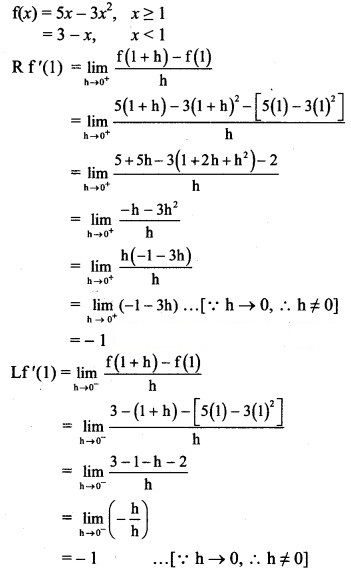
Here, Lf'(1) = Rf'(1)
∴ f(x) is differentiable at x = 1.
Question 9.
Solution: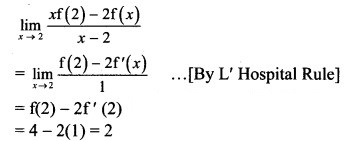
Question 10.
Solution:
